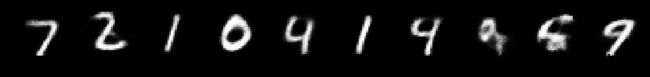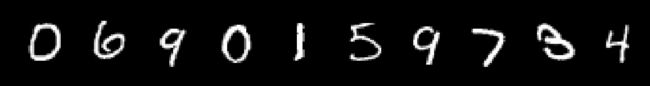【Deep Learning】Autoencoders
Orignal: link
最近在学习图网络内容,涉及到了自动编码器,需要一些预备的知识。本期,推送自编码器内容。
Definition
不同的资料中给Autoencoders的定义不同,下为一些资料中的定义
Definition 1
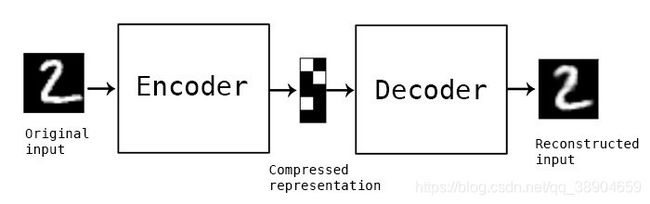
An autoencoder is a neural network that is trained to attempt to copy its input to its output.
Definition 2
An autoencoder is a type of artificial neural network used to learn efficient data codings in an unsupervised manner. The aim of an autoencoder is to learn a representation (encoding) for a set of data, typically for dimensionality reduction, by training the network to ignore signal “noise”.
Definition 3
Autoencoder is an unsupervised artificial neural network that learns how to efficiently compress and encode data then learns how to reconstruct the data back from the reduced encoded representation to a representation that is as close to the original input as possible.
总之,autoencoders就是神经网络的一种,由一个encoder和一个decoder组成。Ecoder相当于对input进行压缩或者编码,decoder则是对隐向量进行重构。
Basic Architecture
Autoencoders主要包括四个部分:
- Encoder: In which the model learns how to reduce the input dimensions and compress the input data into an encoded representation.
- Input: x ∈ R d = X {\pmb x} \in \mathbb{R}^d = \mathcal{X} xxx∈Rd=X
- Output: h ∈ R p = F {\pmb h} \in \mathbb{R}^p = \mathcal{F} hhh∈Rp=F
- Weight matrix: W ∈ R p × d {\bf W}\in \mathbb{R}^{p \times d} W∈Rp×d
- Bias vector: b ∈ R p {\pmb b} \in \mathbb{R}^p bbb∈Rp
- Activation function: σ ( ⋅ ) \sigma(\cdot) σ(⋅)
h = σ ( W x + b ) {\pmb h} = \sigma({\bf W}{\pmb x} + {\pmb b}) hhh=σ(Wxxx+bbb)
Weights and biases are usually initialized randomly, and then updated iteratively during training through Backpropagation.
-
Bottleneck: which is the layer that contains the compressed representation of the input data. This is the lowest possible dimensions of the input data.
-
Decoder: In which the model learns how to reconstruct the data from the encoded representation to be as close to the original input as possible.
- Input: h ∈ R p = F {\pmb h} \in \mathbb{R}^p = \mathcal{F} hhh∈Rp=F
- Output: x ′ ∈ R d = X {\pmb x'} \in \mathbb{R}^d = \mathcal{X} xxx′∈Rd=X
- Weight matrix: W ′ ∈ R d × p {\bf W'}\in \mathbb{R}^{d \times p} W′∈Rd×p
- Bias vector: b ′ ∈ R d {\pmb b'} \in \mathbb{R}^d bbb′∈Rd
- Activation function: σ ′ ( ⋅ ) \sigma'(\cdot) σ′(⋅)
x ′ = σ ′ ( W ′ h + b ′ ) {\pmb x'} = \sigma'({\bf W'} {\pmb h} + {\pmb b'}) xxx′=σ′(W′hhh+bbb′)
- Reconstruction Loss: This is the method that measures measure how well the decoder is performing and how close the output is to the original input.
KaTeX parse error: No such environment: equation* at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲*̲}̲\begin{aligned}…
如前所述,自动编码器的训练是通过误差的反向传播来完成的,就像常规的前馈神经网络一样。
An example of autoencoders
以MNIST数据集为例,使用一个简单的前馈神经网络,建立一个6层网络模型如下例程:
import numpy as np
import keras
from keras.datasets import mnist
from keras.models import Sequential, Model
from keras.layers import Dense, Input
from keras import optimizers
from keras.optimizers import Adam
(x_train, y_train), (x_test, y_test) = mnist.load_data()
train_x = x_train.reshape(60000, 784) / 255
val_x = x_test.reshape(10000, 784) / 255
autoencoder = Sequential()
autoencoder.add(Dense(512, activation='elu', input_shape=(784,)))
autoencoder.add(Dense(128, activation='elu'))
autoencoder.add(Dense(10, activation='linear', name="bottleneck"))
autoencoder.add(Dense(128, activation='elu'))
autoencoder.add(Dense(512, activation='elu'))
autoencoder.add(Dense(784, activation='sigmoid'))
autoencoder.compile(loss='mean_squared_error', optimizer = Adam())
trained_model = autoencoder.fit(train_x, train_x, batch_size=1024, epochs=10, verbose=1, validation_data=(val_x, val_x))
encoder = Model(autoencoder.input, autoencoder.get_layer('bottleneck').output)
encoded_data = encoder.predict(train_x) # bottleneck representation
decoded_output = autoencoder.predict(train_x) # reconstruction
encoding_dim = 10
# return the decoder
encoded_input = Input(shape=(encoding_dim,))
decoder = autoencoder.layers[-3](encoded_input)
decoder = autoencoder.layers[-2](decoder)
decoder = autoencoder.layers[-1](decoder)
decoder = Model(encoded_input, decoder)
绘制出loss
import matplotlib.pyplot as plt
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.rc('font', size = 16)
epochs = 10
loss = trained_model.history['loss']
val_loss = trained_model.history['val_loss']
epochs = range(epochs)
plt.figure()
plt.plot(epochs, loss, 'bo-', label='Training loss')
plt.plot(epochs, val_loss, 'rs-', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
正如您在图中看到的,验证集的最后一次重构损失/错误是0.0194,这已经很好了。
试验数据预测
import matplotlib.pyplot as plt
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.rc('font', size = 16)
plt.figure(figsize=(20, 4))
print("Test Images")
for i in range(10):
plt.subplot(2, 10, i+1)
plt.imshow(x_test[i], cmap='gray')
curr_lbl = y_test[i]
plt.title("(Label: " + str(curr_lbl) + ")")
plt.show()
plt.figure(figsize=(20, 4))
print("Reconstruction of Test Images")
pred = decoded_output.reshape(10000, 28, 28)
for i in range(10):
plt.subplot(2, 10, i+1)
plt.imshow(pred[i], cmap='gray')
plt.show()
Denoising Autoencoder
一个例程,运行时间较长
import numpy as np
import keras
from keras.datasets import mnist
from keras.models import Sequential, Model
from keras.layers import Input, Conv2D, MaxPooling2D, UpSampling2D
from keras import optimizers
from keras.optimizers import Adam
from sklearn.model_selection import train_test_split
# Plot
import matplotlib.pyplot as plt
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.rc('font', size = 16)
batch_size = 128
epochs = 100
inChannel = 1
x, y = 28, 28
input_img = Input(shape = (x, y, inChannel))
(X_train, y_train), (X_test, y_test) = mnist.load_data()
x_train = X_train.reshape(60000, x, y, inChannel) / 255
x_test = X_test.reshape(10000, x, y, inChannel) / 255
# x_train = x_train[0 : 10000]
# y_train = y_train[0 : 10000]
train_X, valid_X, train_Y, valid_Y = train_test_split(x_train,
y_train, test_size=0.4, random_state=13)
test_data = x_test
noise_factor = 0.5
x_train_noisy = train_X + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_X.shape)
x_valid_noisy = valid_X + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=valid_X.shape)
x_test_noisy = test_data + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=test_data.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_valid_noisy = np.clip(x_valid_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
def autoencoder(input_img):
#encoder
conv1 = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
pool1 = MaxPooling2D(pool_size=(2, 2))(conv1)
conv2 = Conv2D(32, (3, 3), activation='relu', padding='same')(pool1)
encoded = MaxPooling2D(pool_size=(2, 2))(conv2)
#decoder
conv3 = Conv2D(32, (3, 3), activation='relu', padding='same')(encoded)
up1 = UpSampling2D((2,2))(conv3)
conv4 = Conv2D(32, (3, 3), activation='relu', padding='same')(up1)
up2 = UpSampling2D((2,2))(conv4)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up2)
return decoded
autoencoder = Model(input_img, autoencoder(input_img))
autoencoder.compile(loss='mean_squared_error', optimizer = Adam())
autoencoder_train = autoencoder.fit(x_train_noisy, train_X,
batch_size=batch_size,
epochs=epochs,
verbose=1,
shuffle=True,
validation_data=(x_valid_noisy, valid_X))
loss = autoencoder_train.history['loss']
valoss = autoencoder_train.history['loss']
val_loss = autoencoder_train.history['val_loss']
epochs = np.linspace(0, epochs - 1, num = epochs)
plt.figure()
plt.plot(epochs, loss, 'b-', label='Training loss')
plt.plot(epochs, val_loss, 'r-', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.grid()
plt.show()
test_labels = y_test
pred = autoencoder.predict(x_test_noisy)
plt.figure(figsize=(20, 4))
print("Test Images")
for i in range(10,20,1):
plt.subplot(2, 10, i+1)
plt.imshow(test_data[i, ..., 0], cmap='gray')
curr_lbl = test_labels[i]
plt.title("(Label: " + str(curr_lbl) + ")")
plt.show()
plt.figure(figsize=(20, 4))
print("Test Images with Noise")
for i in range(10,20,1):
plt.subplot(2, 10, i+1)
plt.imshow(x_test_noisy[i, ..., 0], cmap='gray')
plt.show()
plt.figure(figsize=(20, 4))
print("Reconstruction of Noisy Test Images")
for i in range(10,20,1):
plt.subplot(2, 10, i+1)
plt.imshow(pred[i, ..., 0], cmap='gray')
plt.show()
Test Images with Noise

Reconstruction of Noisy Test Images

Variational autoencoder
![]()
Unlike classical (sparse, denoising, etc.) autoencoders, Variational autoencoders (VAEs) are generative models, like Generative Adversarial Networks
变分自编码器内容将在后期专门推送。