leetcode51

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。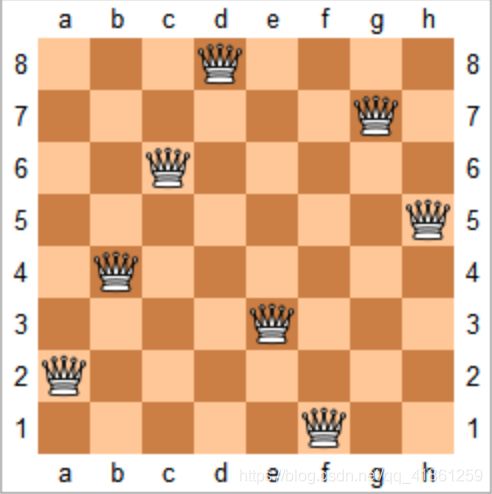

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

解法一：

首先拿到这个题，很自然的就想到了DFS + 回溯，因为我们要进行排列组合，尝试每一种情况，记录符合条件的解法，但是需要注意的是，在n值小的情况下，可以使用DFS，如果n值较大，程序是会调用溢出的，只能采用其他的方法，当然这个题是没有问题的

此题的解法中需要注意的项：

• 我们采用n值大小的数组来记录Q皇后的位置,下标代表行，值代表列，
  如图：代表第0行，第一列有Q，依次。。。。。

判断点是否和前面的点在同一列，这个比较好做

判断在一条右对角线的方法是如点A（2，-1）B（-1，0），如果两点横坐标相减等于纵坐标相减，则处于右对角线，舍弃

判断在一条左对角线的方法是如点A（a:1，b:0）B（c:2，d:-1），如果c - a = d - b,则说明在左对角线，舍弃

当以上条件都通过，则是一个有效的皇后点

代码如下：

class Solution {
    public List> solveNQueens(int n) {

        List> res = new ArrayList<>();
        //下标i与值 v形成key-value，代表皇后Q放在第i行v列
        int [] placeQueen = new int[n];
        //参数分别是，行，总行，位置标记，结果记录
        DFS(0,n,placeQueen,res);
        return res;
    }

    private void DFS(int row, int n, int[] placeQueen, List> res) {
        if (row >= n){
            //每一个位置都符合了过后，就需要将这种解法的位置记录下来
            List list = new ArrayList<>();
            for (int i = 0; i < n; i++) {
                String s = "";
                for (int col = 0; col < n; col++) {
                    if (placeQueen[i] == col){
                        s+="Q";
                    }else{
                        s+=".";
                    }
                }
                list.add(s);
            }
            res.add(list);
            return;
        }
        //尝试row行的所有列
        for (int col = 0; col < n; col++) {
            //如果所在的行和列有效
            if (isValid(placeQueen,row,col)){
                //标记row ，col
                placeQueen[row] = col;
                DFS(row+1,n,placeQueen,res);
                //按照正常的逻辑，这里需要对placequeen的值进行回溯，这里不需要，直接在下一次循环时进行了更改
            }
        }

    }

    private boolean isValid(int [] placeQueen ,int row, int col) {

        //这里判断斜线的方法感觉不容易想到
        for (int i = 0; i < row ; i++) {
            //如果这个位置与之前某个在同一列
            int pos = placeQueen[i];
            if (pos == col){
                return false;
            }
            //在之前某个点的右对角线
            if (i - row == pos-col){
                return false;
            }
            //在之前的某个点的左对角线
            if (row+col == i + pos){
                return false;
            }
        }
        return true;
    }
}

解法二：第二种方法，我们就以52题为例吧！两个题大体的思想都是一样的。第二种方法就很不容易想到了，那就是使用位运算，针对第一种方法的缺点，这种方法显然NB很多，应该是最好的解法。

思路：例如我们最开始的pie na col都是0

pie :      0 0 0 0

 na :      0 0 0 0

Col :      0 0 0 0
那么一行诡异的代码出现了，这就是核心代码，int bits = (~(col|pie|na)) & ((1<

代码如下：

class Solution {
          int count = 0;
    public int totalNQueens(int n) {
        if (n<1){
            return 0;
        }
        //参数代码意思：n行数，然后是row，col，pie（左对角线），na（右对角线）
        DFS(n,0,0,0,0);
        return count;
    }

    private void DFS(int n, int row, int col, int pie, int na) {
        if (row >= n){
            count++;
            return;
        }
        //这行代码可能比较难理解，思路中说吧
        int bits = (~(col|pie|na)) & ((1<>1);
            //bits最后一个1使用过后，去掉bits中的最后一个1，一般去掉最后一个1就是&自己-1
            bits = bits & (bits-1);
        }

    }
}