棋盘覆盖(SDIBTOJ 2000)
棋盘覆盖(SDIBTOJ 2000)
算法实验1:棋盘覆盖
Time Limit: 1 Sec Memory Limit: 64 MB
Submit: 3677 Solved: 977
Description
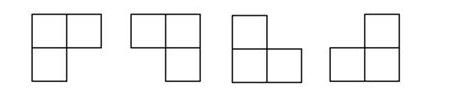
在一个 2 k 2^k 2k x 2 k 2^k 2k 个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
Input
k,dr,dc。k定义如前,dr,dc分别表示特殊方格所在的行号和列号 1 ≤ k ≤ 6 1 \leq k \leq 6 1≤k≤6
Output
按照左上,右上,左下,右下的顺序用分治法求解。特殊方格标0,其他位置按上述顺序依次标记。
Sample Input
2 1 1
Sample Output
2 2 3 3
2 0 1 3
4 1 1 5
4 4 5 5
HINT
Source
http://acm.sdibt.edu.cn/JudgeOnline/problem.php?id=2000
分治法:
分–将问题分解为规模更小的子问题
治–将这些规模更小的子问题逐个击破
合–将已解决的子问题合并,最终得出“母”问题的解
本题可分为两种情况:
若当前棋盘格数小于等于4,则
(1)直接向标记位及未标记位填数即可
若当前棋盘的格数大于4,则
(2)将此棋盘均分成四个较小的正方形棋盘,按照从上到下、从左到右的顺序判断每个小正方形棋盘,方别记为1号、2号、3号、4号棋盘
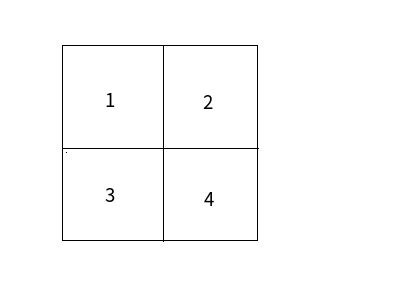
若1~4号中某个小棋盘中有被标记的点,这直接调用fenzhi函数
若1号小棋盘中无被标记的点,则将其右下角的点赋值并作为被标记点调用fenzhi函数
若2号小棋盘中无被标记的点,则将其左下角的点赋值并作为被标记点调用fenzhi函数
若3号小棋盘中无被标记的点,则将其右上角的点赋值并作为被标记点调用fenzhi函数
若4号小棋盘中无被标记的点,则将其左上角的点赋值并作为被标记点调用fenzhi函数
AC的代码
c++版
#include python版
from __future__ import print_function
import sys
lcou = 1
board = [[0 for i in range(100)] for i in range(100)]
def fenzhi(nr, nc, dr, dc, size):
global lcou
if size == 1:
return
s = size / 2
k = lcou
lcou += 1
if dr < nr + s and dc < nc + s:
fenzhi(nr, nc, dr, dc, s)
else:
board[nr + s - 1][nc + s - 1] = k
fenzhi(nr, nc, nr + s - 1, nc + s - 1, s)
if dr < nr + s and dc >= nc + s:
fenzhi(nr, nc + s, dr, dc, s)
else:
board[nr + s - 1][nc + s] = k
fenzhi(nr, nc + s, nr + s - 1, nc + s, s)
if dr >= nr + s and dc < nc + s:
fenzhi(nr + s, nc, dr, dc, s)
else:
board[nr + s][nc + s - 1] = k
fenzhi(nr + s, nc, nr + s, nc + s - 1, s)
if dr >= nr + s and dc >= nc + s:
fenzhi(nr + s, nc + s, dr, dc, s)
else:
board[nr + s][nc + s] = k
fenzhi(nr + s, nc + s, nr + s, nc + s, s)
k, dr, dc = map(int, sys.stdin.readline().split())
size = pow(2, k)
fenzhi(0, 0, dr, dc, size)
for i in range(0, size):
for j in range(0, size):
print(board[int(i)][int(j)], end='')
print(' ', end='')
if i != size-1:
print('')