【论文笔记】CycleMorph：使用循环一致性的2D/3D/多尺度微分同胚图像配准模型

本文是论文《CycleMorph: Cycle Consistent Unsupervised Deformable Image Registration》的阅读笔记。

现有的既又深度学习的配准方法通常不能保证拓扑保持（preservation of topology），为了解决这个问题，文章提出了一个名为CycleMorph的模型，使用循环一致性来提供一个隐式的正则来保留拓扑结构。此外，该模型可以实现2D或3D图像以及多尺度图像的配准。

一、相关工作

1. CycleMorph使用循环一致性来

在该模型中训练两个卷积神经网络$G_X$和$G_Y$，$G_X$产生从源域图像到目标域图像的正向形变场${\varphi }_{XY}$，$G_Y$产生从目标域图像到源域图像的逆向形变场${\varphi }_{YX}$。

为了解决3D图像太大而导致显存放不下的情况，采用了先对下采样的图像进行粗糙的大变形，然后再对局部的patch进行变形。

2. 微分同胚图像配准

在经典的变分图像配准方法中，配准问题的能量方程可以表示为：
$$\mathcal{L}(X,Y,\varphi )={\mathcal{L}}_{sim}(\mathcal{T}(X,\varphi ),Y)+{\mathcal{L}}_{reg}(\varphi )$$
其中，$X,Y$分别表示浮动图像和固定图像，$\varphi$表示位移向量场，$\mathcal{T}$表示根据形变场$\varphi$将$X$变形到$Y$的变换函数（空间变换层），${\mathcal{L}}_{sim}$是衡量图像相似性的相似项，${\mathcal{L}}_{reg}$是使得形变场平滑的正则项。

微分同胚图像配准为向量场$\varphi$施加了一个约束，使得可变形映射是微分同胚。微分同胚变形保证了两个图像之间的变形是连续、可微、拓扑保持的。微分同胚图像配准算法的例子有LDDMM和SyN。

无监督的图像配准方法通常没有为一致性增加一个约束，从而可能会产生形变场重叠的问题。

3. 一致性图像配准

当参数有限时，微分同胚图像配准算法中的形变场通常是离散的。因此，估计的形变$F:X\mapsto Y$和估计的形变$R:Y\mapsto X$的逆是不相等的。在一致性图像配准中，这个问题通过逆一致性$R\simeq F^{-1}$而减轻了。

二、CycleMorph

上图是CycleMorph网络的结构示意图。

1. 损失函数

模型通过优化以下损失函数来训练：
$$\underset{G_X,G_Y}{\min }\mathcal{L}\left(X,Y,G_X,G_Y\right)$$
其中
$$\begin{array}{rl}\mathcal{L}\left(X,Y,G_X,G_Y\right)=& {\mathcal{L}}_{regist}\left(X,Y,G_X\right)\\ & +{\mathcal{L}}_{regist}\left(Y,X,G_Y\right)\\ & +\alpha {\mathcal{L}}_{cycle}\left(X,Y,G_X,G_Y\right)\\ & +\beta {\mathcal{L}}_{identity}\left(X,Y,G_X,G_Y\right)\end{array}$$

上图是网络中三个损失的示意图。${\mathcal{L}}_{regist}$是配准损失，它包括图像相似性损失和形变场的正则项损失两部分，图像相似性采用的是局部互相关，正则项损失采用的是$L_2$正则损失，所以
$$\begin{array}{l}{\mathcal{L}}_{\text{regist}}\left(X,Y,G_X\right)\\ =-\left(\mathcal{T}\left(X,{\varphi }_{XY}\right)\otimes Y\right)+\lambda \sum {\Vert \nabla {\varphi }_{XY}\Vert }^2\end{array}$$
其中$\lambda$是超参数，$\otimes$表示局部互相关，其定义为：
$$A\otimes B=\sum _{\mathbf{v}\in \Omega }\frac{{\left({\sum }_{{\mathbf{v}}_i}\left(A\left({\mathbf{v}}_i\right)-\bar{A}(\mathbf{v})\right)\left(B\left({\mathbf{v}}_i\right)-\bar{B}(\mathbf{v})\right)\right)}^2}{\left({\sum }_{{\mathbf{v}}_i}{\left(A\left({\mathbf{v}}_i\right)-\bar{A}(\mathbf{v})\right)}^2\right)\left({\sum }_{{\mathbf{v}}_i}{\left(B\left({\mathbf{v}}_i\right)-\bar{B}(\mathbf{v})\right)}^2\right)}$$
其中，$\Omega$表示整个3D图像，$\bar{A}(v)$和$\bar{B}(v)$表示图像$A(v)$和$B(v)$的局部均值，$v_i$迭代在体素$v$周围大小为$w\times w\times w$（2D图像时为$w\times w$）的范围迭代计算，其中$w=9$。

${\mathcal{L}}_{cycle}$是循环一致性损失，源域图像$X$先通过$G_X$被配准得到$\hat{Y}$，再通过$G_Y$配准得到$\tilde{X}$，计算$X$和$\tilde{X}$之间的循环一致性损失；同理目标域图像$Y$先通过$G_Y$被配准得到$\hat{X}$，再通过$G_X$配准得到$\tilde{Y}$，计算$Y$和$\tilde{Y}$之间的循环一致性损失。上述过程可以表示为：
$$(X,Y)\simeq \left(\mathcal{T}\left(\hat{Y},{\hat{\varphi }}_{YX}\right),\mathcal{T}\left(\hat{X},{\hat{\varphi }}_{XY}\right)\right)$$
其中
$$(\hat{Y},\hat{X}):=\left(\mathcal{T}\left(X,{\varphi }_{XY}\right),\mathcal{T}\left(Y,{\varphi }_{YX}\right)\right)$$
所以，循环一致性损失可以通过下式计算：
$$\begin{array}{l}{\mathcal{L}}_{\text{cycle}}\left(X,Y,G_X,G_Y\right)\\ ={\Vert \mathcal{T}\left(\hat{Y},{\hat{\varphi }}_{YX}\right)-X\Vert }_1+{\Vert \mathcal{T}\left(\hat{X},{\hat{\varphi }}_{XY}\right)-Y\Vert }_1\end{array}$$
其中，$\Vert \cdot {\Vert }_1$表示$L_1$范式。

${\mathcal{L}}_{identity}$是恒等损失表示当固定图像和浮动图像为同一个时，两者之间不会有任何变形。因此该损失避免了不必要的变形，使得形变场在静态区域的预测更加稳定。该损失可以表示为：
$$\begin{array}{l}{\mathcal{L}}_{\text{identity}}\left(X,Y,G_X,G_Y\right)\\ =-\left(\mathcal{T}\left(Y,G_X(Y,Y)\right)\otimes Y\right)-\left(\mathcal{T}\left(X,G_Y(X,X)\right)\otimes X\right)\end{array}$$
其中$\otimes$表示局部互相关。

2. 空间变换层

对于3D图像来说，使用三线性插值，可以表示为：
$$\begin{array}{l}\mathcal{T}(X,\varphi )\\ ={\sum }_{q\in \mathcal{N}(p+\varphi (p))}X(q){\prod }_{d\in \{i,j,k\}}\left(1-\left|p_d+\varphi \left(p_d\right)-p_d\right|\right)\end{array}$$
其中，$p$表示像素下标，$\mathcal{N}(p+\varphi (p))$表示在$p+\varphi (p)$周围的8像素的立方体邻居，$d$是3D图像空间的三个方向。当为2D图像配准时，采用的是双线性插值。

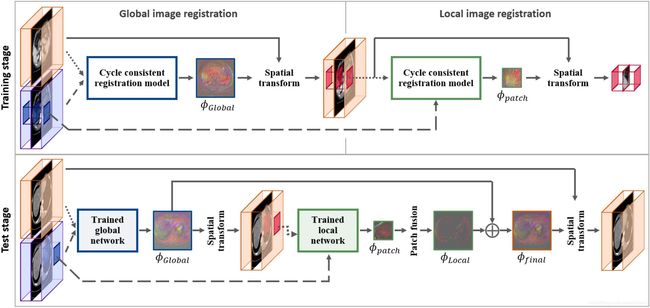
3. 多尺度配准

上图是多尺度配准的示意图，训练时多尺度配准采用先做全局配准，后做局部配准。全局图像配准模型首先在下采样的图像对上进行训练，然后通过对形变场进行上采样得到全尺寸的变形后的图像，然后对变形后图像的patch进行局部图像配准的训练。

在测试阶段，由于要进行两次线性插值，所以两个配准网络会导致误差的累计，从而降低配准的精度。所以采取了全局配准和局部配准先得到各自的形变场，然后再将形变场相加，只做一次线性插值。

三、实验

1. 数据集

三个任务三个数据集，2D配准任务使用的是面部表情图像Radboud Faces Database（RaFD）数据集，3D配准任务使用的是OASIS-3脑部MRI数据集，多尺度配准使用的是肝脏CT数据集。不同任务所采用的参数就不再赘述。

实验采用的baseline有Elastix，SyN，VoxelMorph和MS-DIRNet。

2. 评价指标

使用形变场的雅克比行列式中非负数的百分比来衡量形变场的重叠程度：
$$\left|J_{\varphi }(\mathbf{v})\right|=|\nabla \varphi (\mathbf{v})|\le 0$$
其中$v$表示体素位置，$|\cdot |$表示矩阵的行列式，当雅克比矩阵的行列式的值都是正数时，形变场是微分同胚的。

在面部表情数据集中有ground-truth标签，衡量其配准后的归一化均方误差损失（NMSE）和结构相似性损失（SSIM）；在脑部MR数据集中有脑部结构的分割标签，衡量其配准后的DICE值，其表达式如下：
$$\mathrm{Dice}(A,B)=\frac{2TP}{2TP+FP+FN}$$
其中$TP,FP,FN$分别表示正阳例、负阳例、负阴例像素的个数。

在肝脏CT数据集中有地标点信息，衡量其在配准后的目标配准损失（TRE），TRE可以通过平均欧几里得距离来计算：
$$TRE(A,B)=\frac{1}{N}\sum _{i=1}^N\Vert a_i-b_i\Vert$$
其中$N$是地标点的数目，$a_i，b_i$是浮动图像和固定图像中第$i$个地标坐标向量。

3. 实验结果

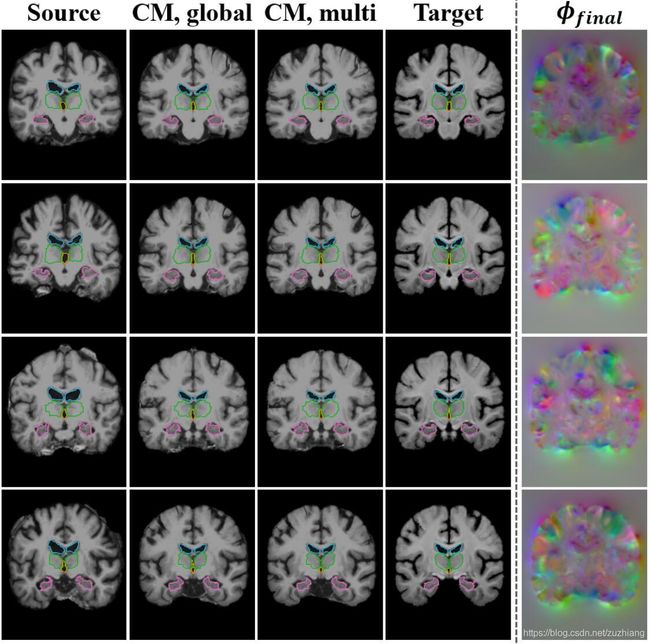
上图是在面部表情数据集上的实验结果。

上图是在脑部MR数据上的配准结果。

上图是不同配准方法在脑部MR数据集上的配准结果的对比表。