曲线拟合(1)——Logistic曲线
To be continue … …
文章目录
-
- 一、Logistic模型
-
- 1.1 Logistic方程概述
- 1.2 Logistic方程的性质
- 二、Logistic曲线拟合方法
-
- 2.1 Logistic曲线初值的选取
- 2.2 Logistic曲线的参数拟合方法
-
- 2.2.1 三点法
- 2.2.2 四点法
- 2.2.3 拐点法
- 2.2.4 误差估计——决定系数
- 2.2.5 非线性拟合
- 三、Logistic预测增长
这是创新训练传染病的
微分方程模型Logistic曲线笔记
一、Logistic模型
Richards曲线拟合方法及初值的选取
1.1 Logistic方程概述
Logistics方程可用下列微分方程描述
{ d N d t = r ( 1 − N N m ) N N ( t 0 ) = N 0 (1) \begin{aligned} \begin{cases} \displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}=r\big(1-\frac{N}{N_{m}}\big)N\\ N(t_{0})=N_{0} \end{cases}\tag{1} \end{aligned} ⎩⎨⎧dtdN=r(1−NmN)NN(t0)=N0(1)
变量分离方程,其中 N m N_{m} Nm表示理论上的最大值, N 0 N_{0} N0表示 t 0 t_{0} t0时刻的病人数
分离变量,得
d N ( 1 − N N m ) N N m = r N m d t \frac{\mathrm{d}N}{(1-\frac{N}{N_{m}})\frac{N}{N_{m}}}=rN_{m}\mathrm{d}t (1−NmN)NmNdN=rNmdt
即
1 N d N − 1 N m − N d ( N m − N ) = r d t \frac{1}{N}\mathrm{d}N-\frac{1}{N_{m}-N}\mathrm{d}(N_{m}-N)=r\mathrm{d}t N1dN−Nm−N1d(Nm−N)=rdt
也就是
ln N − ln ( N m − N ) = r t + C ′ ⇒ ln ( N N m − N ) = r t + C ′ ⇒ N N m − N = C e r t ( 其 中 , C = e C ′ ) ⇒ N = N m 1 + 1 / C ⋅ e − r t \begin{aligned} &\ln N-\ln(N_{m}-N)=rt+C'\\ &\Rightarrow \ln(\frac{N}{N_{m}-N})=rt+C'\\ &\Rightarrow \frac{N}{N_{m}-N}=C\mathrm{e}^{rt}(其中,C=\mathrm{e}^{C'})\\ &\Rightarrow N=\frac{N_{m}}{1+1/C\cdot\mathrm{e}^{-rt}} \end{aligned} lnN−ln(Nm−N)=rt+C′⇒ln(Nm−NN)=rt+C′⇒Nm−NN=Cert(其中,C=eC′)⇒N=1+1/C⋅e−rtNm
代入初值条件 N ( t 0 ) = N 0 N(t_{0})=N_{0} N(t0)=N0,得
C = N 0 N m − N 0 e − r t 0 C=\frac{N_{0}}{N_{m}-N_{0}}\mathrm{e}^{-rt_{0}} C=Nm−N0N0e−rt0
代入上式得
N = N m 1 + ( N m N 0 − 1 ) e − r ( t − t 0 ) ⇒ N = 1 1 N m + ( 1 N 0 − 1 N m ) e − r ( t − t 0 ) (2) \begin{aligned} & N=\frac{N_{m}}{1+(\frac{N_{m}}{N_{0}}-1)\mathrm{e}^{-r(t-t_{0})}}\\ & \Rightarrow N=\frac{1}{\frac{1}{N_{m}}+(\frac{1}{N_{0}}-\frac{1}{N_{m}})\mathrm{e}^{-r(t-t_{0})}}\tag{2} \end{aligned} N=1+(N0Nm−1)e−r(t−t0)Nm⇒N=Nm1+(N01−Nm1)e−r(t−t0)1(2)
由上式可看出,令 t → ∞ t\to\infty t→∞, N → N m N\to N_{m} N→Nm,也即
N = N 0 N m e r ( t − t 0 ) N 0 ( e r ( t − t 0 ) − 1 ) + N m N=\frac{N_{0}N_{m}\mathrm{e}^{r(t-t_{0})}}{N_{0}(\mathrm{e}^{r(t-t_{0})}-1)+N_{m}} N=N0(er(t−t0)−1)+NmN0Nmer(t−t0)
另外一种形式的logistic微分方程如下
{ d N d t = r N − k N 2 N ( t 0 ) = N 0 (3) \begin{aligned} \begin{cases} \displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}=rN-kN^{2}\\ N(t_{0})=N_{0} \end{cases}\tag{3} \end{aligned} ⎩⎨⎧dtdN=rN−kN2N(t0)=N0(3)
其中, r r r表示
发病率, k k k表示预防效果
同理即得
N = 1 k r + ( 1 N 0 − k r ) e − r ( t − t 0 ) N=\frac{1}{\frac{k}{r}+(\frac{1}{N_{0}}-\frac{k}{r})\mathrm{e}^{-r(t-t_{0})}} N=rk+(N01−rk)e−r(t−t0)1
其中, N m = r k , ( w h i l e t → ∞ ) N_{m}=\frac{r}{k},(while\ t\to\infty) Nm=kr,(while t→∞),表示理论上的最大人数
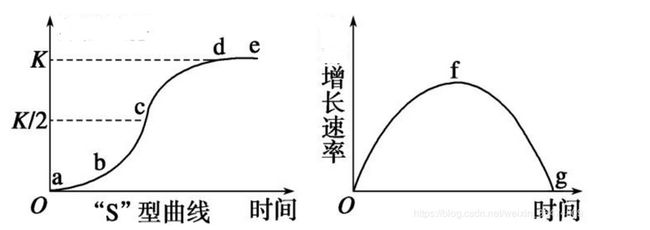
1.2 Logistic方程的性质
由 d N d t = − k N 2 + r N \frac{\mathrm{d}N}{\mathrm{d}t}=-kN^{2}+rN dtdN=−kN2+rN的右端函数,不妨设为 f ( N ) f(N) f(N),则
易知 f > 0 f>0 f>0对 N ∈ ( 0 , N m ) N\in(0,N_{m}) N∈(0,Nm)恒成立,函数图像为开口向下的抛物线
也就是 d N d t > 0 \frac{\mathrm{d}N}{\mathrm{d}t}>0 dtdN>0对 N ∈ ( 0 , N m ) N\in(0,N_{m}) N∈(0,Nm)恒成立,也即 N ( t ) N(t) N(t)在 ( 0 , N m ) (0,N_{m}) (0,Nm)单调递增
又因为 f ′ = − 2 k N + r f'=-2kN+r f′=−2kN+r,即 f ′ ( N m / 2 ) = 0 f'(N_{m}/2)=0 f′(Nm/2)=0;当 N < N m 2 N<\frac{N_{m}}{2} N<2Nm时, f ′ > 0 f'>0 f′>0,当 N > N m 2 N>\frac{N_{m}}{2} N>2Nm时, f ′ < 0 f'<0 f′<0。即表明当 N < N m 2 N<\frac{N_{m}}{2} N<2Nm时,增长率 d N d t \frac{\mathrm{d}N}{\mathrm{d}t} dtdN是增加的,当 N > N m 2 N>\frac{N_{m}}{2} N>2Nm时,增长率是减小的。在 N = N m 2 N=\frac{N_{m}}{2} N=2Nm时,增长率 d N d t \frac{\mathrm{d}N}{\mathrm{d}t} dtdN达到最大。可看成疫情
拐点的到来。且当 t → ∞ t\to\infty t→∞时, N → N m N\to N_{m} N→Nm。
由上式,代入 N = N m 2 N=\frac{N_{m}}{2} N=2Nm,求得时间 t t t,即
t = 1 r ln ( N m N 0 − 1 ) + t 0 = 1 r ln ( r k N 0 − 1 ) + t 0 (4) t=\frac{1}{r}\ln(\frac{N_{m}}{N_{0}}-1)+t_{0}=\frac{1}{r}\ln(\frac{r}{kN_{0}}-1)+t_{0}\tag{4} t=r1ln(N0Nm−1)+t0=r1ln(kN0r−1)+t0(4)
即为疫情出现拐点的可能时间 t t t。
二、Logistic曲线拟合方法
对于logistic曲线的参数拟合方法,见参考文献
-
Matlab拟合logistic曲线
-
Wikipedia Logistic function
-
python实现logistic增长模型拟合2019-nCov确诊人数2月1日更新
拟合的初值选取方法等
2.1 Logistic曲线初值的选取
对于如下一组数据
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 日期 | 11 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| 感染人数 | 41 | 45 | 62 | 291 | 440 | 571 | 830 | 1287 | 1975 | 2744 | 4515 | 5974 | 7711 | 9692 | 11791 |
用
logistic曲线拟合
用形如 A / ( 1 + b e − c t ) A/(1+b\mathrm{e}^{-ct}) A/(1+be−ct)拟合
Matlab拟合
clear
clc
x=1:15;
y=[41,45,62,291,440,571,830,1287,1975,2744,4515,5974,7711,9692,11791];
% syms b c
% [b,c]=solve(5000/(1+b*exp(-c*1))==43,5000/(1+b*exp(-c*2))==45,b,c)
c0=[5000,120.6896,0.0459];
% c0=[6000 145.0271 0.0458];c0=[10000 242.3770 0.0457];
fun=inline('c(1)./(1+c(2).*exp(-c(3).*x))','c','x');
b=nlinfit(x,y,fun,c0);disp("各参数的值(c(1) c(2) c(3)):");disp(b);
t=0:0.1:30;
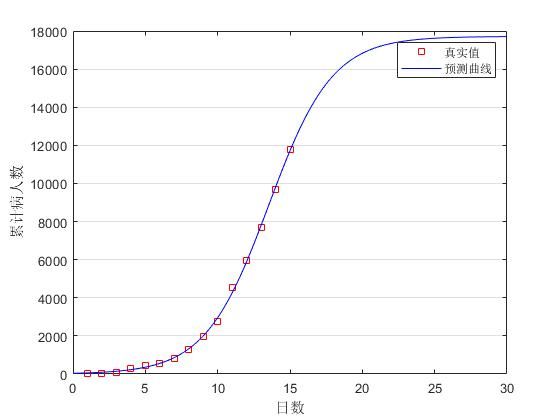
plot(x,y,'rs',t,fun(b,t),'b');set(gca,'ygrid','on');
legend("真实值","预测曲线");xlabel("日数");ylabel("累计病人数");
对于A的初值选取,可任意选取 A 0 = 5000 A_{0}=5000 A0=5000,将初值 F ( 1 ) = 43 , F ( 2 ) = 45 F(1)=43,F(2)=45 F(1)=43,F(2)=45代入
syms b c
[b,c]=solve(5000/(1+b*exp(-c*1))==43,5000/(1+b*exp(-c*2))==45,b,c)
解得: C 0 = [ 5000 , b , c ] C_{0}=[5000,b,c] C0=[5000,b,c],此即非线性拟合
即得logistic方程如下
N = 17715 1 + 473 ⋅ e − 0.4553 t N=\frac{17715}{1+473\cdot\mathrm{e}^{-0.4553t}} N=1+473⋅e−0.4553t17715
python拟合
一般来说, r r r越小,累计病人数增多,且结束的时间长;反之亦然
同理,利用非线性最小二乘法python
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
''' 给定一组数据,利用非线性曲线拟合方法
拟合Logistic方程
'''
plt.style.use('ggplot') #使用ggplot绘图风格
#plt.rcdefaults() #恢复默认画图方式
#给出一组数据
x=np.array(range(1,16))
x1=np.array(range(1,31))
y=np.array([41,45,62,291,440,571,830,1287,1975,2744,4515,5974,7711,9692,11791])
plot1=plt.plot(x,y,'x',label="confirm")
c0=np.array([5000,120.6896,0.0459])#一组初值
def func(x,a,b,c):
result=a/(1+b*np.exp(-c*x))
return result
p_est,err_est=curve_fit(func,x,y,c0)
#print(p_est)
plot2=plt.plot(x1,func(x1,*p_est), "-",label="curve-fitting")
plt.legend(loc=0) #指定legend的位置右上角
plt.xlabel("day");plt.ylabel("people") #增加x,y标签
2.2 Logistic曲线的参数拟合方法
主要参考文献
- 殷祚云.Logistic曲线拟合方法研究[J].数理统计与管理,2002(01):41-46.
- 主要包括(
线性或非线性):三点法、四点法和拐点法
Logistic方程为
N = N m 1 + e b − r t (5) N=\frac{N_{m}}{1+\mathrm{e}^{b-rt}}\tag{5} N=1+eb−rtNm(5)
其中,N为生物量,r为
内禀自然增长率, N m N_{m} Nm为环境容纳量,b为积分常数
将上式取对数,整理得
ln N m − N N = b − r t (6) \ln\frac{N_{m}-N}{N}=b-rt\tag{6} lnNNm−N=b−rt(6)
2.2.1 三点法
假设有实测数据 Q = { ( t 1 , N 1 ) , ( t 2 , N 2 ) , ⋯ , ( t n , N n ) } Q=\left\{(t_{1},N_{1}),(t_{2},N_{2}),\cdots,(t_{n},N_{n})\right\} Q={ (t1,N1),(t2,N2),⋯,(tn,Nn)},分别选取数据Q的始点、中点和终点数据,即 A ( T 1 , N T 1 ) , B ( T 2 , N T 2 ) , ( C T 3 , N T 3 ) A(T_{1},N_{T_{1}}),B(T_{2},N_{T_{2}}),(C_{T_{3},N_{T_{3}}}) A(T1,NT1),B(T2,NT2),(CT3,NT3),代入(6)得
{ ln N m − N 1 N 1 = b − r T 1 ① ln N m − N 2 N 2 = b − r T 2 ② ln N m − N 3 N 3 = b − r T 3 ③ (7) \begin{aligned} \begin{cases} \ln\frac{N_{m}-N_{1}}{N_{1}}=b-rT_{1}\ \ \ ① \\ \ln\frac{N_{m}-N_{2}}{N_{2}}=b-rT_{2}\ \ \ ② \\ \ln\frac{N_{m}-N_{3}}{N_{3}}=b-rT_{3}\ \ \ ③ \end{cases}\tag{7} \end{aligned} ⎩⎪⎨⎪⎧lnN1Nm−N1=b−rT1 ①lnN2Nm−N2=b−rT2 ②lnN3Nm−N3=b−rT3 ③(7)
其中 2 T 2 = T 1 + T 2 2T_{2}=T_{1}+T_{2} 2T2=T1+T2,由①+③-2②整理得
2 ln N − N T 2 N T 2 = ln N − N T 1 N T 1 + ln N − N T 3 N T 3 2\ln\frac{N-N_{T_{2}}}{N_{T_{2}}}=\ln\frac{N-N_{T_{1}}}{N_{T_{1}}}+\ln\frac{N-N_{T_{3}}}{N_{T_{3}}} 2lnNT2N−NT2=lnNT1N−NT1+lnNT3N−NT3
化简得
N m ( 1 N 2 2 − 1 N 1 N 3 ) = − N 1 + N 3 N 2 + 2 N 2 N_{m}(\frac{1}{N_{2}^{2}}-\frac{1}{N_{1}N_{3}})=-\frac{N_{1}+N_{3}}{N_{2}}+\frac{2}{N_{2}} Nm(N221−N1N31)=−N2N1+N3+N22
整理得
N m = 2 N 1 N 2 N 3 − N 2 2 ( N 1 + N 3 ) N 1 N 3 − N 2 2 (8) N_{m}=\frac{2N_{1}N_{2}N_{3}-N_{2}^{2}(N_{1}+N_{3})}{N_{1}N_{3}-N_{2}^{2}}\tag{8} Nm=N1N3−N222N1N2N3−N22(N1+N3)(8)
如上对于表1数据,可取 A ( t 初 = 1 , 41 ) , B ( t 中 = 8 , 1287 ) , C ( t 终 = 15 , 11791 ) A(t_{初}=1,41),B(t_{ {中}}=8,1287),C(t_{ {终}}=15,11791) A(t初=1,41),B(t中=8,1287),C(t终=15,11791),代入(2)式得 N m = 15648 N_{m}=15648 Nm=15648。此时对于(1)式用最小二乘法做线性拟合,即形如 y = b − r t y=b-rt y=b−rt。
最小二乘法估计公式:设有一列点 ( x i , y i ) , i = 1 , 2 , ⋯ , n (x_{i},y_{i}),i=1,2,\cdots,n (xi,yi),i=1,2,⋯,n,利用 y = a x + b y=ax+b y=ax+b估计
{ a ˉ = n ∑ i = 1 n x i y i − ( ∑ i = 1 n x i ) ( ∑ i = 1 n y i ) n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 b ˉ = ( ∑ i = 1 n x i 2 ) ( ∑ i = 1 n y i ) − ( ∑ i = 1 n x i y i ) ( ∑ i = 1 n x i ) n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 \begin{aligned} \begin{cases} \displaystyle \bar{a}=\frac{n\sum_{i=1}^{n}x_{i}y_{i}-(\sum_{i=1}^{n}x_{i})(\sum_{i=1}^{n}y_{i})}{n\sum_{i=1}^{n}x_{i}^{2}-(\sum_{i=1}^{n}x_{i})^{2}}\\\\ \displaystyle \bar{b}=\frac{(\sum_{i=1}^{n}x_{i}^{2})(\sum_{i=1}^{n}y_{i})-(\sum_{i=1}^{n}x_{i}y_{i})(\sum_{i=1}^{n}x_{i})}{n\sum_{i=1}^{n}x_{i}^{2}-(\sum_{i=1}^{n}x_{i})^{2}} \end{cases} \end{aligned} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧aˉ=n∑i=1nxi2−(∑i=1nxi)2n∑i=1nxiyi−(∑i=1nxi)(∑i=1nyi)bˉ=n∑i=1nxi2−(∑i=1nxi)2(∑i=1nxi2)(∑i=1nyi)−(∑i=1nxiyi)(∑i=1nxi)
对于原始数据Q做变换得
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 变换后 | 5.9419 | 5.8486 | 5.5270 | 3.9660 | 3.5428 | 3.2735 | 2.8822 | 2.4122 | 1.9349 | 1.5481 | 0.9025 | 0.4820 | 0.0289 | -0.4869 | -1.1174 |
这是线性拟合
利用
cftool线性最小二乘法拟合求得 r = 0.5042 , b = 6.4793 r=0.5042,b=6.4793 r=0.5042,b=6.4793
clear
clc
t=1:15;
N=[41 45 62 291 440 571 830 1287 1975 2744 4515 5974 7711 9692 11791];
K=15648;
NN=log(K./N-1);
plot(t,N,'s');set(gca,'ygrid','on');
p=polyfit(t,NN,1)
2.2.2 四点法
假设有实测数据 Q = { ( t 1 , N 1 ) , ( t 2 , N 2 ) , ⋯ , ( t n , N n ) } Q=\left\{(t_{1},N_{1}),(t_{2},N_{2}),\cdots,(t_{n},N_{n})\right\} Q={ (t1,N1),(t2,N2),⋯,(tn,Nn)},分别选取数据Q的始点、中点两点和终点共四个数据,即 A ( T 1 , N 1 ) , B ( T 2 , N 2 ) , C ( T 3 , N 3 ) , D ( T 4 , N 4 ) A(T_{1},N_{1}),B(T_{2},N_{2}),C({T_{3},N_{3}}),D(T_{4},N_{4}) A(T1,N1),B(T2,N2),C(T3,N3),D(T4,N4),代入(i)得,
{ ln N m − N 1 N 1 = b − r T 1 ⓐ ln N m − N 2 N 2 = b − r T 2 ⓑ ln N m − N 3 N 3 = b − r T 3 ⓒ ln N m − N 4 N 4 = b − r T 4 ⓓ (9) \begin{aligned} \begin{cases} \ln\frac{N_{m}-N_{1}}{N_{1}}=b-rT_{1}\ \ \ ⓐ \\ \ln\frac{N_{m}-N_{2}}{N_{2}}=b-rT_{2}\ \ \ ⓑ\\ \ln\frac{N_{m}-N_{3}}{N_{3}}=b-rT_{3}\ \ \ ⓒ \\ \ln\frac{N_{m}-N_{4}}{N_{4}}=b-rT_{4}\ \ \ ⓓ \end{cases}\tag{9} \end{aligned} ⎩⎪⎪⎪⎨⎪⎪⎪⎧lnN1Nm−N1=b−rT1 ⓐlnN2Nm−N2=b−rT2 ⓑlnN3Nm−N3=b−rT3 ⓒlnN4Nm−N4=b−rT4 ⓓ(9)
其中 T 1 + T 4 = T 2 + T 3 T_{1}+T_{4}=T_{2}+T_{3} T1+T4=T2+T3,由 ⓑ + ⓒ − ⓐ − ⓓ ⓑ+ⓒ-ⓐ-ⓓ ⓑ+ⓒ−ⓐ−ⓓ得
ln N m − N 2 N 2 + ln N m − N 3 N 3 = ln N m − N 1 N 1 + ln N m − N 4 N 4 \ln\frac{N_{m}-N_{2}}{N_{2}}+\ln\frac{N_{m}-N_{3}}{N_{3}}=\ln\frac{N_{m}-N_{1}}{N_{1}}+\ln\frac{N_{m}-N_{4}}{N_{4}} lnN2Nm−N2+lnN3Nm−N3=lnN1Nm−N1+lnN4Nm−N4
整理得
N m ( 1 N 2 N 3 − 1 N 1 N 4 ) = N 2 + N 3 N 2 N 3 − N 1 + N 4 N 1 N 4 N_{m}(\frac{1}{N_{2}N_{3}}-\frac{1}{N_{1}N_{4}})=\frac{N_{2}+N_{3}}{N_{2}N_{3}}-\frac{N_{1}+N_{4}}{N_{1}N_{4}} Nm(N2N31−N1N41)=N2N3N2+N3−N1N4N1+N4
即
N m = N 1 N 4 ( N 2 + N 3 ) − N 2 N 3 ( N 2 + N 3 ) N 1 N 4 − N 2 N 3 (10) N_{m}=\frac{N_{1}N_{4}(N_{2}+N_{3})-N_{2}N_{3}(N_{2}+N_{3})}{N_{1}N_{4}-N_{2}N_{3}}\tag{10} Nm=N1N4−N2N3N1N4(N2+N3)−N2N3(N2+N3)(10)
同理,对于表1的数据,可取 A ( t 初 = 1 , 41 ) , B ( t = 6 , 571 ) A(t_{ {初}}=1,41),B(t=6,571) A(t初=1,41),B(t=6,571), C ( t = 10 , 2744 ) C(t=10,2744) C(t=10,2744), D ( t 终 = 15 , 11791 ) D(t_{ {终}}=15,11791) D(t终=15,11791),计算可得 N m = 15632 N_{m}=15632 Nm=15632。此时对于(1)式用最小二乘法做线性拟合
2.2.3 拐点法
拐点的另外一种求法
对于方程
d N d t = r ( 1 − N N m ) N \frac{\mathrm{d}N}{\mathrm{d}t}=r(1-\frac{N}{N_{m}})N dtdN=r(1−NmN)N
左右两边对 t t t求导数,即
d 2 N d t = r ( 1 − 2 N N m ) d N d t (12) \frac{\mathrm{d}^{2}N}{\mathrm{d}t}=r(1-\frac{2N}{N_{m}})\frac{\mathrm{d}N}{\mathrm{d}t}\tag{12} dtd2N=r(1−Nm2N)dtdN(12)
当 d N d t ≠ 0 \frac{\mathrm{d}N}{\mathrm{d}t}\neq0 dtdN=0时,即得 d 2 N d t = 0 ⇒ N = N m 2 \frac{\mathrm{d}^{2}N}{\mathrm{d}t}=0\Rightarrow N=\frac{N_{m}}{2} dtd2N=0⇒N=2Nm,即当 d N d t \frac{\mathrm{d}N}{\mathrm{d}t} dtdN最大时,也就是曲线
斜率最大处时 N k = N m 2 N_{k}=\frac{N_{m}}{2} Nk=2Nm,即 N m = 2 N k N_{m}=2N_{k} Nm=2Nk。曲线由凸变凹。
2.2.4 误差估计——决定系数
一个特定数值对于其平均值的偏离,称为离差。决定系数的定义公式为
R 2 = S S R S S T = ∑ ( y ^ − y ˉ ) 2 ∑ ( y − y ˉ ) 2 = 1 − ∑ ( y − y ^ ) 2 ∑ ( y − y ˉ ) 2 R^{2}=\frac{SSR}{SST}=\frac{\sum(\hat{y}-\bar{y})^{2}}{\sum(y-\bar{y})^{2}}=1-\frac{\sum(y-\hat{y})^{2}}{\sum(y-\bar{y})^{2}} R2=SSTSSR=∑(y−yˉ)2∑(y^−yˉ)2=1−∑(y−yˉ)2∑(y−y^)2
2.2.5 非线性拟合
任意取A的一个初值 A 0 A_{0} A0,然后利用两个方程求解另两个参数的初值
syms b c
[b,c]=solve(5000/(1+b*exp(-c*1))==43,5000/(1+b*exp(-c*2))==45,b,c)
由上两式
{ 5000 / ( 1 + b ∗ e x p ( − c ∗ 1 ) ) = = 43 5000 / ( 1 + b ∗ e x p ( − c ∗ 2 ) ) = = 45 \begin{aligned} \begin{cases} 5000/(1+b*exp(-c*1))==43\\ 5000/(1+b*exp(-c*2))==45 \end{cases} \end{aligned} { 5000/(1+b∗exp(−c∗1))==435000/(1+b∗exp(−c∗2))==45然后用L-M方法据梯度降速求得最优参数。
该方程组有唯一解,据
克拉默法则,取对数后系数矩阵不等于0,对应上述Matlab拟合方法。