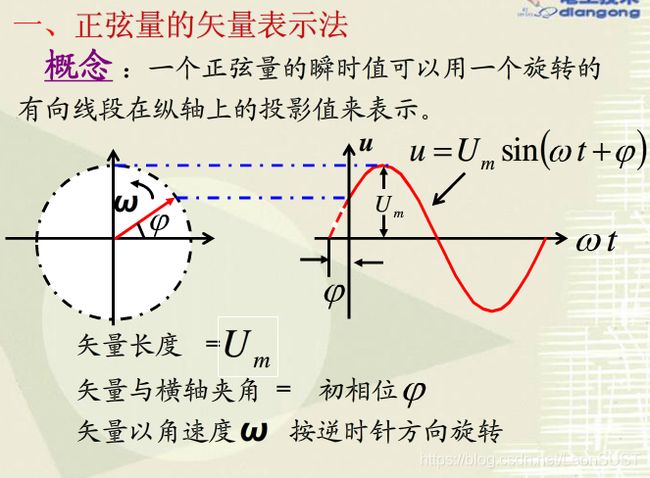
三相正弦交流量超前滞后关系分析 图文并茂(〃'▽'〃)
超前滞后 说了很久 都没有认真的思考过 到底什么是超前 什么是滞后 ~~ 还是思考的少。。。这么简单的问题都没有屡清楚 真是尴尬
自己看的云里雾里的 So 总结一下三相的超前滞后 方便之后的学习 看资料可以快速理解
进人正题
三相正弦交流量超前滞后关系分析
1. 从表达式分析超前滞后关系
三相电压的表达式为:
u A O ( t ) = U m sin ω t = 2 U sin ω t u B O ( t ) = U m sin ( ω t − 12 0 ∘ ) = 2 U sin ( ω t − 12 0 ∘ ) u C O ( t ) = U m sin ( ω t − 24 0 ∘ ) = 2 U sin ( ω t − 24 0 ∘ ) = U m sin ( ω t + 12 0 ∘ ) = 2 U sin ( ω t + 12 0 ∘ ) \begin{array}{l}{u_{{\rm{AO}}}}(t) = {U_m}\sin \omega {\rm{ }}t = \sqrt 2 U\sin \omega {\rm{ }}t\\ {u_{{\rm{BO}}}}(t) = {U_m}\sin (\omega {\rm{ }}t - {120^ \circ }) = \sqrt 2 U\sin (\omega {\rm{ }}t - {120^ \circ }) \\{u_{{\rm{CO}}}}(t) = {U_m}\sin (\omega {\rm{ }}t - {240^ \circ }) = \sqrt 2 U\sin (\omega {\rm{ }}t - {240^ \circ }) = {U_m}\sin (\omega {\rm{ }}t + {120^ \circ }) = \sqrt 2 U\sin (\omega {\rm{ }}t + {120^ \circ }) \end{array} uAO(t)=Umsinωt=2UsinωtuBO(t)=Umsin(ωt−120∘)=2Usin(ωt−120∘)uCO(t)=Umsin(ωt−240∘)=2Usin(ωt−240∘)=Umsin(ωt+120∘)=2Usin(ωt+120∘)
同频率正弦量的相位差 :
设 u ( t ) = U m sin ( ω t + ψ u ) i ( t ) = I m s i n ( ω t + ψ i ) \begin{array}{l} u(t) = {U_m}\sin (\omega {\rm{ }}t + {\psi _{\rm{u}}})\\ i{\rm{(t)}} = {I_{\rm{m}}}{\rm{sin}}(\omega {\rm{t}} + {\psi _{\rm{i}}}) \end{array} u(t)=Umsin(ωt+ψu)i(t)=Imsin(ωt+ψi)
则 相位差表示为 :
ϕ = ( ω t + ψ u ) − ( ω t + ψ i ) = ψ u − ψ i \phi = (\omega t + {\psi _u}){\rm{ - }}(\omega t + {\psi _i}) = {\psi _u}{\rm{ - }}{\psi _i} ϕ=(ωt+ψu)−(ωt+ψi)=ψu−ψi
我们规定 ∣ ϕ ∣ < 18 0 ∘ | \phi | < 180 ^\circ ∣ϕ∣<180∘
ϕ > 0 , u 超 前 i ϕ 角 , 或 i 滞 后 u 角 , ( u 比 i 先 到 达 最 大 值 ) \phi >0,u超前i \phi 角,或i滞后u 角,(u比i先到达最大值) ϕ>0,u超前iϕ角,或i滞后u角,(u比i先到达最大值)
ϕ < 0 , u 滞 后 i ϕ 角 , 或 i 超 前 u 角 , ( u 比 i 先 到 达 最 大 值 ) \phi <0,u滞后i \phi 角,或i超前u 角,(u比i先到达最大值) ϕ<0,u滞后iϕ角,或i超前u角,(u比i先到达最大值)
** 综上,A相超前B相120°,B超前C相180°,C相超前A相120° **
2. 从波形图判断超前滞后关系:
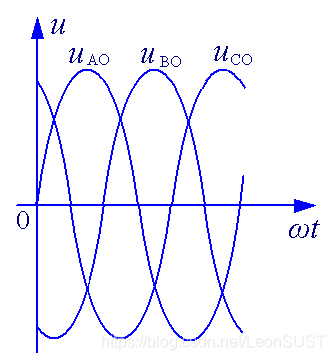
从上面得知相位差即为正弦量初相位之差
( t = 0 时 ) , ϕ > 0 , u 超 前 i ϕ 角 , 或 i 滞 后 u ϕ 角 , ( u 比 i 先 到 达 最 大 值 ) ; (t=0时),\phi> 0, u超前i \phi 角,或i滞后u \phi 角,(u比i先到达最大值); (t=0时),ϕ>0,u超前iϕ角,或i滞后uϕ角,(u比i先到达最大值);
ϕ < 0 , u 滞 后 i ϕ 角 , 或 i 超 前 u ϕ 角 , ( i 比 u 先 到 达 最 大 值 ) 。 \phi<0,u滞后i \phi 角,或i超前u \phi 角,(i比u先到达最大值)。 ϕ<0,u滞后iϕ角,或i超前uϕ角,(i比u先到达最大值)。
所 以 判 断 依 据 就 是 从 t = 0 时 刻 开 始 , 所以判断依据就是从t=0时刻开始, 所以判断依据就是从t=0时刻开始,
那个正弦量先到达最大值就是超前,否则就为滞后。
所 以 u A O 超 前 u B O , u B O 超 前 u C O , u C O 超 前 u A O 。 所以u_{AO}超前u_{BO},u_{BO}超前u_{CO},u_{CO}超前u_{AO}。 所以uAO超前uBO,uBO超前uCO,uCO超前uAO。
3. 从向量图判断超前滞后关系
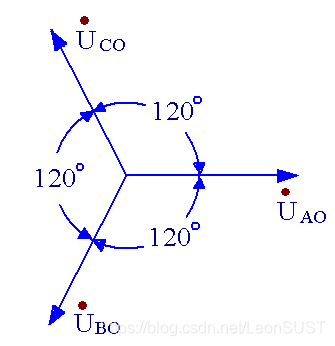
这 个 问 题 就 回 归 到 初 始 角 Ψ 和 相 位 差 的 判 断 这个问题就回归到初始角 \Psi 和相位差的判断 这个问题就回归到初始角Ψ和相位差的判断
在 向 量 图 中 如 果 U A O 与 横 坐 标 轴 重 合 , 则 U C O 和 U A O 的 相 位 差 为 120 ° , C 相 超 前 A 相 120 度 。 在向量图中如果U_{AO}与横坐标轴重合,则U_{CO}和U_{AO}的相位差为120°,C相超前A相120度。 在向量图中如果UAO与横坐标轴重合,则UCO和UAO的相位差为120°,C相超前A相120度。
U B O 和 U A O 的 相 位 差 为 240 ° , 由 于 相 位 差 绝 对 值 小 于 180 ° , 所 以 将 相 位 差 转 化 为 − 120 ° ( 240 ° − 360 ° ) , 即 A 相 超 前 B 相 120 ° 。 U_{BO}和U_{AO}的相位差为240°,由于相位差绝对值小于180°,所以将相位差转化为-120°(240°-360°),即A相超前B相120°。 UBO和UAO的相位差为240°,由于相位差绝对值小于180°,所以将相位差转化为−120°(240°−360°),即A相超前B相120°。
同 理 可 得 B 相 超 前 C 相 120 ° 。 同理可得B相超前C相120°。 同理可得B相超前C相120°。