栈的应用——四则运算表达式求值（Java实现）

首先介绍几个概念

中缀式：平常我们所用到的标准的四则运算表达式就是中缀式，如9+(3-1)*3+10/2,这就是一个中缀式

后缀式（逆波兰式）：一种不需要括号的后缀表达法，我们也把他称为逆波兰式，如将上面的中缀式改为后缀式则是：9 3 1 - 3 * + 10 2 / +。

    通过观察中缀式发现，括号都是成对出现的，有左括号就一定有右括号，对于多重括号，最终也是完全嵌套匹配的。这用栈的结构存储正好合适，只要碰到左括号，就将左括号入栈，不管表达式有多少重括号，反正遇到左括号就入栈，而后面出现的右括号时，就让栈顶的左括号出栈，期间让数字进行运算，这样，最终有括号的表达式从左到右巡查一遍，栈应该是由空到有元素，最终再因全部匹配成功后成为空栈。

注：以下都以表达式 9 + ( 3 - 1 ) * 3 + 10 / 2来讲解

如何将中缀式改为后缀式呢？？？

    规则：从左到右遍历中缀式的每个数字和符号，若是数字就输出，即成为后缀式的一部分；若是符号，则判断其与栈顶符号的优先级，是右括号或者优先级不高于栈顶符号（即乘除优先加减），则栈顶元素一次出栈并输出，并将当前符号入栈，直到最终输出后缀式为止。

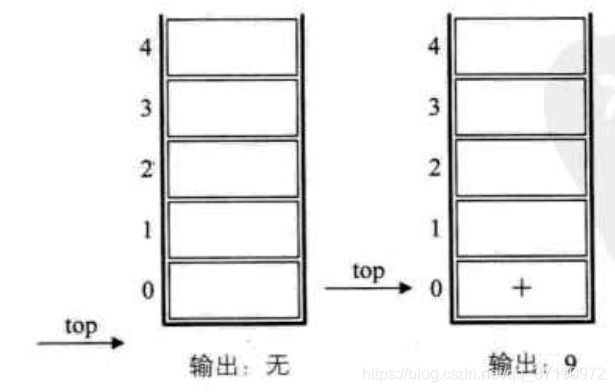
1. 初始化一空栈，用来对符号入出栈使用，如下左图所示
2. 第一个字符是数字9，输出9，后面是符号‘+’入栈，如下右图所示

     3.第三个字符是‘（ ’，依然是符号，因其只是左括号，还未配对，故入栈，如下左图所示

     4.第四个字符是数字3，输出，总表达式为9 3，接着是‘-’，入栈，如下右图所示

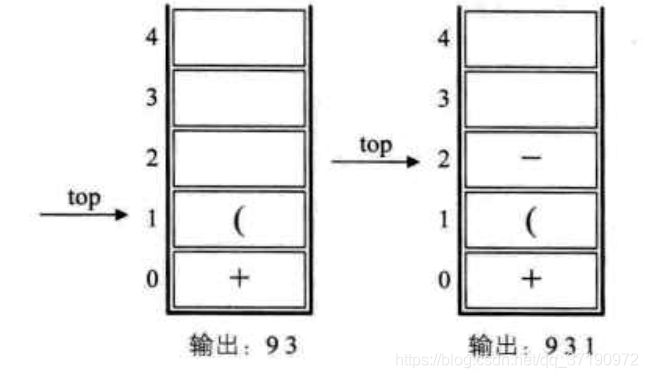
      5.接下来是数字1，输出，总表达式是9 3 1，后面是符号‘  ）’，此时，我们需要去匹配此前的‘（  ’，所以栈顶一次出栈，并输出，直到‘（  ’出栈为止。此时左括号上方只有‘-’，因此输出‘-’。总的输出表达式为9 3 1 -，如下左图所示。

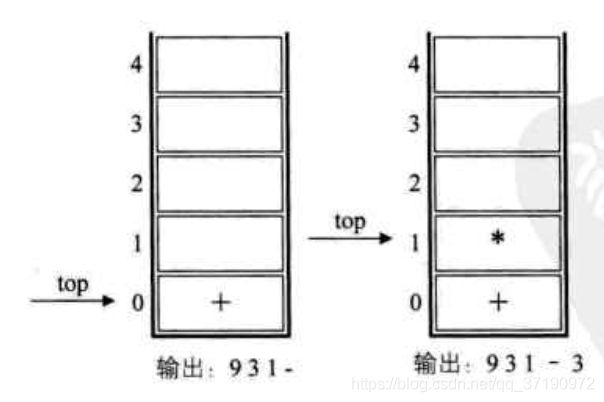
     6.紧接着是符号‘*’，因为此时的栈顶符号是‘+’，优先级低于‘*’，因此不输出，‘*’入栈，接着是数字3，输出，总的表达式为9 3 1 - 3。如下右图所示。

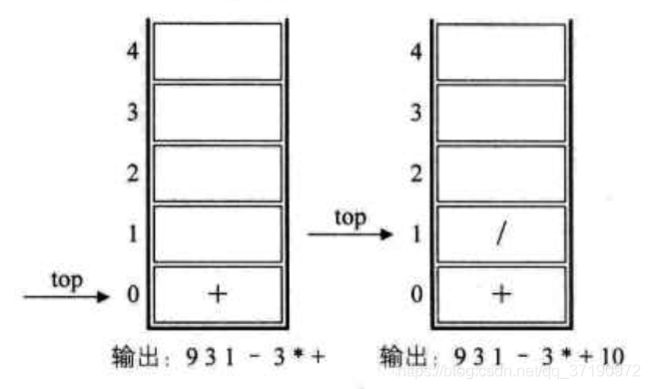
       7.之后是符号‘+’，此时当前元素栈顶元素‘*’比‘+’优先级高，因此栈中元素出栈并输出（没有比‘+’优先级更低的了，所以全部出栈），总输出为9 3 1 - 3 * +，然后将当前的这个符号‘+’入栈，也就是说，前6张图的栈底的‘+’是指中缀式开头的9后面的那个‘+’，而下左图栈底的‘+’是指9+（3-1）*3+中的最后一个‘+’。

       8.紧接着是数字10，输出，总表达式为9 3 1 - 3 * + 10.后是符号‘/’，入栈，如下右图所示

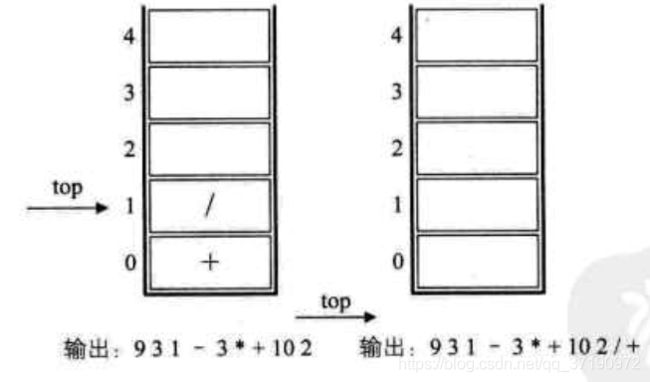
        9.最后一个数字2，输出，总表达式为9 3 1 - 3 * + 10 2，如下左图所示。

        10.因已经到了最后，所以将栈中符号全部出栈并输出，最终输出的后缀表达式结果是9 3 1 - 3  * + 10 2 / +，如下右图所示。

Java代码：

package infixForm;


import java.util.*;

class input {
    //public ArrayList rpnArr = new ArrayList<>(); //用于存储逆波兰式
    int flag = 0;   //用于记录存储的顺序
    public Map intMap = new HashMap<>();  //用于存储数字
    public Map charMap = new HashMap<>();  //用于存储运算符
    private Map map = new HashMap<>();    /*用于存四则运算符号的优先级*/
    private ArrayList sum = new ArrayList<>();   /*可能不是一位数字，那么就需要对每个数字线存储起来，遇到符号时就将存储起来的数字进行运算*/
    private Stack stack = new Stack<>();   /*存储四则运算的符号*/
    private int add = 0;



    /*对每个字符进行相应的处理*/
    public void analyze(String arithmetic) {
        /*定义四则运算符号的优先级*/
        map.put('+', 1);
        map.put('-', 1);
        map.put('*', 2);
        map.put('/', 2);
        map.put('(', 3);
        map.put(')', 3);

        for (int i = 0; i < arithmetic.length(); i++) {
            char nowChar = arithmetic.charAt(i);    /*取出第一个字符*/
            if (nowChar == '+' || nowChar == '-' || nowChar == '*' || nowChar == '/' || nowChar == '(' || nowChar == ')') { /*如果是运算符，就要准备入栈了*/
                if (sum.size() != 0) {    /*入栈之前要先将存储在sum里的数据输出出来*/
                    summation();
                }

                if (nowChar != ')' && (stack.empty() || map.get(nowChar) > map.get(stack.peek()) || stack.peek() == '(')) {    /*入栈*/
                    stack.push(nowChar);
                } else {
                    while (!stack.isEmpty() && nowChar >= map.get(stack.peek())) {  /*当栈不为空并且当前运算符的优先级不小于栈顶运算符时*/
                        if (stack.peek() == '(' || stack.peek() == ')') {   /*对于括号运行符不需要进行输出*/
                            stack.pop();
                            break;
                        }

                        charMap.put(flag++, stack.pop());
                    }

                    if (nowChar != ')') {       /*将当前运算符入栈，如果是右括号的话就不用入栈了，因为当遇到右括号是，栈里面必然有左括号，所以右括号要随着左括号一起丢掉*/
                        stack.push(nowChar);
                    }
                }
                continue;
            } else {    /*当不是运算符时，就进行数字的处理*/
                int num = Integer.valueOf(nowChar) - 48;    /*Integer.valueOf(nowChar)输出的是字符的ASCII码值，要将它转化为实际数字*/
                sum.add(num);   /*可能不是一位数，所以可以先将该数字存储起来*/
            }
        }

        if (sum.size() != 0) {  /*此时sum里面可能还会有存储起来的数字，但还没输出，此时要进行输出了*/
            for (int j = 0; j < sum.size(); j++) {
                summation();
            }
        }

        while (!stack.isEmpty()) {  /*和上面的原因一样*/
            charMap.put(flag++, stack.pop());
        }
    }

    /*将数组中的数字求和*/
    public void summation() {
        int pow = 0;
        for (int j = sum.size() - 1; j >= 0; j--) {
            add = (int) (add + sum.get(j) * Math.pow(10, pow++));   /*求幂运算*/
        }
        sum.clear();    /*清除ArrayList集合*/
        intMap.put(flag++, add);
        add = 0;    /*归零，不然下次会接着累加*/
    }
}

得到了后缀式，那么如何由后缀式计算出结果呢？

      规则：从左到右遍历表达式的每个数字和字符，遇到是数字就入栈，遇到树符号，就将处于栈顶的两个数字出栈，进行运算，运算结果入栈，一直到最终获得结果。

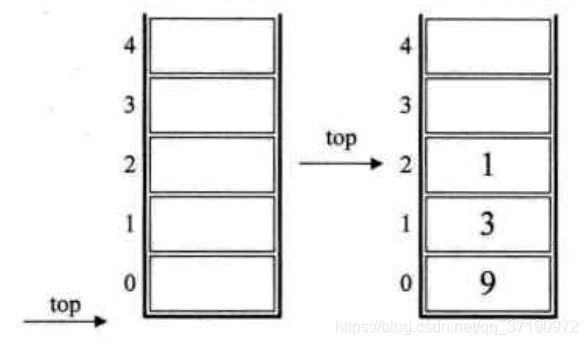
     1.初始化一个空栈，此栈用来对要运算的数字进出使用，如下左图所示。

     2.后缀式中的前三个都是数字，所以9 3 1入栈，如下右图所示。

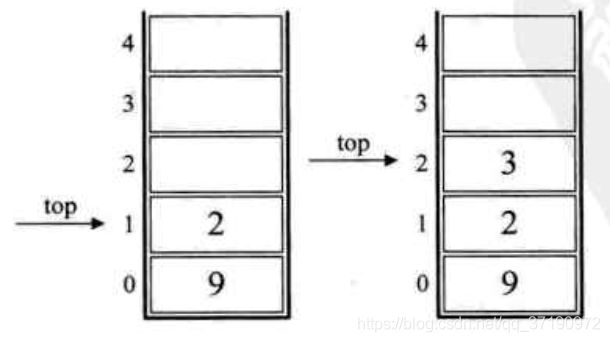
     3.接下来是‘-’，所以将栈中的1出栈作为减数，3出栈作为被减数，并运算3-1得到2，再将2入栈，如下左图所示

     4.接着是数字3入栈，如下右图所示

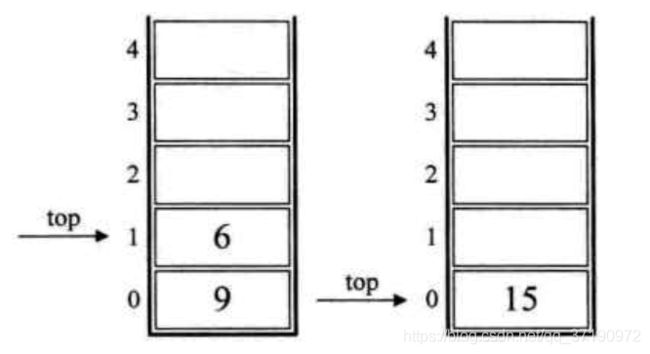
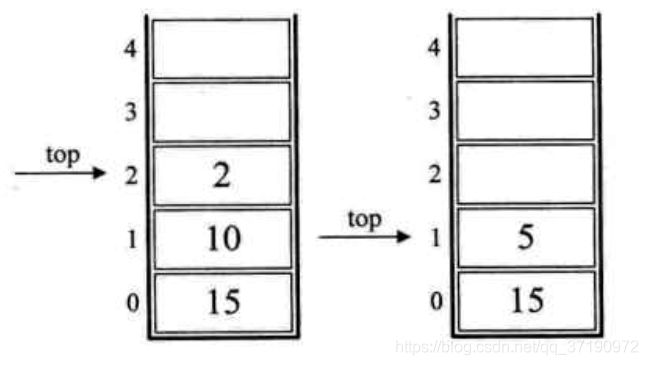
     5.后面是‘*’，也就意味着栈中的3和2出栈，2和3相乘，得到6，并将6入栈，如下左图所示

     6.下面是‘+’，所以栈中的6和9出栈，9和6相加，得到15，将15入栈，如下右图所示 

     7.接着是10和2两数字入栈，如下左图所示

     8.接下来是符号‘/’，因此，栈顶的2和10出栈，10和2相除，得到5，将5入栈，如下右图所示

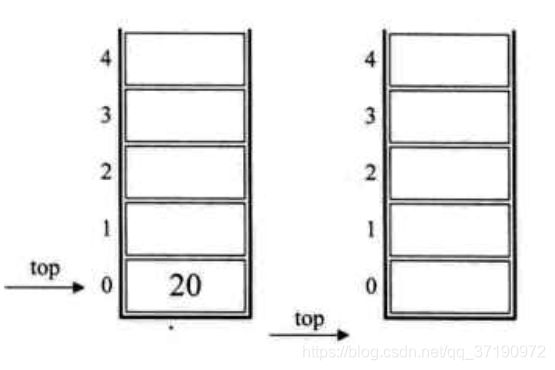
      9.最后一个是符号‘+’，所以15和5出栈并相加，得到20，将20入栈，如下左图所示

      10.结果是20入栈，栈变为空，如下右图所示

Java代码：

package infixForm;

import java.util.Map;
import java.util.Scanner;
import java.util.Stack;

public class output {
    private static input in = new input();
    public static void main(String[] args) {
        //String arithmetic = "6+(8-7)+5*6+9-12/2";   /*输入的表达式*/
        Scanner scanner = new Scanner(System.in);
        String arithmetic = scanner.next();
        in.analyze(arithmetic);
        operation(in.intMap, in.charMap);
    }

    public static void operation(Map intMap, Map characterMap) {
        Stack stack = new Stack<>();   /*用于存放数据*/

        for (int i = 0; i < in.intMap.size() + in.charMap.size(); i++) {    /*遍历两个集合*/
            if (in.intMap.get(i) == null) {
                switch (in.charMap.get(i)) {
                    case '-':   /*因为是减号，所以要考虑顺序*/
                        int one = stack.pop();
                        int two = stack.pop();
                        stack.push(two - one);
                        break;
                    case '+':
                        stack.push(stack.pop() + stack.pop());
                        break;
                    case '*':
                        stack.push(stack.pop() * stack.pop());
                        break;
                    case '/':   /*同减号，是因为顺序*/
                        int first = stack.pop();
                        int second = stack.pop();
                        stack.push(second / first);
                        break;
                }
            } else {
                stack.push(in.intMap.get(i));
            }
        }
        System.out.print("结果是：" + stack.pop());

    }
}

运行结果：

 

总结：

从以上推导中可以看出，想要计算机具有处理我们通常的标准（中缀）表达式的能力，最重要的就是两步：

• 将中缀式转化为后缀式（栈用来进出运算符）。
• 将后缀式进行运算得到结果（栈用来进出运算的数字）。