P问题、NP问题、NPC问题的概念及实例证明
美剧《基本演绎法》（也就是美版“福尔摩斯”）第 2 季第 2 集中，两位研究 NP 问题的数学家被谋杀了，凶手是同行，因为被害者即将证明“P=NP 问题”，她为独吞成果而下了毒手。然而凶手的动机，并不是千禧年大奖难题那100万美元的奖金——解决了 P=NP 问题，就能够破译世界上所有的密码系统，这里面的利益比100万美元多多了。
剧中只用了一句话来介绍 P=NP 的意义：“能用电脑快速验证一个解的问题，也能够用电脑快速地求出解”。这句过于简单的话可能让大家一头雾水，今天我们就来讲一讲 P vs. NP。
-
- 几种问题及其关系
- 规约一种技巧
- 如何对问题证明
- NP-Complete间的规约例子
-
- 3SATIndependent Set
- 3SAT Vertex Cover
- 3SAT ILP
- 3SAT Hamiltonian cycle problem
- Subset sum problem Partition problem
- Clique problemSubgraph isomorphism problem
- Partition problem Knapsack problem
- Vertex Cover Independent Set
- Independent Set Clique problem
- Hamiltonian cycle problem Hamiltonian path problem
- Hamiltonian cycle problem Traveling salesman problem
-
- 参考资料
几种问题及其关系
首先解释一下什么是NP问题，什么是NP hard问题，什么是NP完全问题。
- P Problem：这个应该最易理解，就是一个问题可以在Polynominal的时间的得到解决，当然，是对于任意input size。
- NP Problem：对于一类问题，我们可能没有一个已知的快速的方法得到问题的答案，但是如果给我们一个candidate answer，我们能够在polynominal的时间内验证这个candidate answer到底是不是我们已知问题的答案，这类问题叫做NP problem。所以很显然 P Problem是NP problem的一个子集。
- NP-hard Problem：对于这一类问题，用一句话概括他们的特征就是“at least as hard as the hardest problems in NP Problem”， 就是NP-hard问题至少和NP问题一样难。
- NP-Complete Problem：对于这一类问题，他们满足两个性质，一个就是在polynomial时间内可以验证一个candidate answer是不是真正的解，另一个性质就是我们可以把任何一个NP问题在polynomial的时间内把他的input转化，使之成为一个NP-complete问题（即规约）。NP-Complete Problem问题可以互相转换 (在多项式时间内)，只要其中一个问题可以在多项式时间内解决，那么其他问题也都将可以在多项式时间内解决。
规约——一种技巧
归约（reduction）： 规约是证明NP-hard问题的一种常用方法，通常用 <= 这个符号来表示。如 P<=Q ，这个就表示P is reducible to Q , or Q is the reduction from P or P is reduced to Q（P问题可以归约到Q问题，or可以把P归约到Q） 。这里的reduction的符号可以当成是 比较难易程度的小于等于号，意味着P至少比Q容易，或者Q至少比P难。
归约主要做的就是以下两个转化（注意两个转化都要在polynomial的时间内完成）【已知 P 是个NP-hard问题，证新问题 Q 亦是NP-hard问题】，
1. 把P的输入转化到Q的输入；
2. 把Q的输出转化到P的输出。
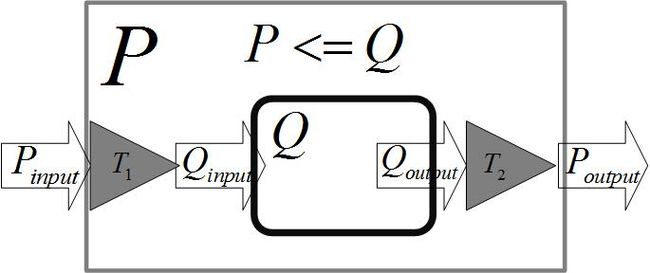
下图展示了上述规约过程。其中 T1 在多项式时间将 P的输入 Pinput 转化成Q的输入 Qinput ; T2 在多项式时间将 Q的输出 Qoutput 转化成P的输出 Poutput 。也就是说NP-hard问题 P 可以依赖于对问题 Q 的解决而解决。那么 Q 至少比 P 要难，即 P<=Q 。
如何对问题证明
下面来列出了一些常见的证明问题及其证明套路。
- 证明NP问题。这个容易，即给你一个结果，你能在polynomial的时间内验证该结果的正确性。
- 证明NP-hard问题。我们要证明一个问题是NP-hard的时候，我们通常要做的是找到一个已被证明了的NPC问题，并把这个NPC问题归约到该问题上去（即NPC<=NP-hard）。
- 证明NP-Complete问题。分以下两步：
- 第一步证明这个问题属于NP；
- 第二步，证明这个问题是NP-hard的。
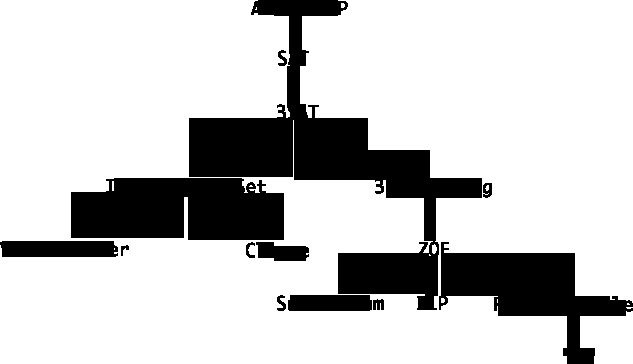
下图列出了几个已被发现NP-Complete问题（更全面的NP-Complete问题列表，见链接A compendium of NP optimization problems，以及List of NP-complete problems），及其规约关系。可以看出所有的NP问题都可以规约到SAT(即NP<=SAT)，也就是说SAT至少与NP问题一样难，或者如果解决了3SAT问题，所有的NP问题就解决了。同样的，SAT<=3SAT，3SAT<=Independent Set，Independent Set<=Vertex Cover OR Clique。
规约关系具有传递性，所以有3SAT<=Vertex Cover，NP<=NP-Complete。 事实上，由于NP-Complete ⊂ NP 且 NP<=NP-Complete，可以推导出 所有的NP-Complete 可以相互规约，也就是所有的NP-Complete都是等价的。
NP-Complete间的规约例子
1. 3SAT<=Independent Set
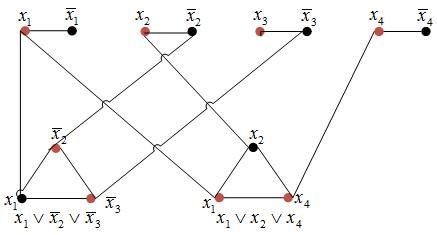
在图G中若顶点集合S满足其中的任意两个顶点之间不存在边，则称S为独立集。The input of Independent Set is a graph G and a number m （独立集问题的两个参数：图 G 以及独立集的大小 m ）, the problem is to find a set of m pairwise non-adjacent vertices(问题是找到 G 的一个大小为 m 的独立集).
转化过程：Given an instance 3SAT problem with m clauses, create an instance (G,m) of Independent Set as follows:
- Graph G has a triangle(edge or vertex) for each clause, with vertices labeled by the clause’s literals
- Add edge between any two vertices that represent opposite literals.
- The goal g is set to the number of clauses.
The graph below corresponding to (x¯∨y∨z¯)∧(x∨y¯∨z)∧(x∨y∨z)∧(x¯∨y¯) (clearly m=3 )
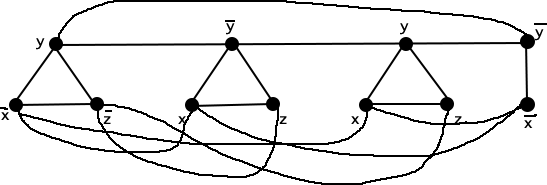
- 假设上图有一个最大独立集，则每个三角形中有且仅有一个顶点在该独立集中，设该顶点取值为1，其余顶点取值0，则其肯定是一个满足的3SAT的赋值。
容易证明该规约过程用了多项式时间。
- 把P的输入转化到Q的输入：P的输入是包含 m 个clause的3SAT表达式；Q的输入当然是转化得到的图形 G 以及独立集的大小参数 g=m 。
- 把Q的输出转化到P的输出：Q的输出是 G 的一个大小为 g 的独立集；P的输出是3SAT的一个赋值。假设 G 中有一个大小为 m 的独立集，则一定是1)三角形内部三个顶点只能取一个 2)不属于三角形的边所连接的顶点也只取一个。对于每个clause，如果选择了 x 对应的顶点，则令 x=1 ，如果选择了 x¯ 对应的顶点，则令 x¯=1 . 则该赋值是满足的。
2. 3SAT <= Vertex Cover
- 图的顶点覆盖（有时是节点覆盖）是一组顶点的集合，使得图的每个边缘至少与集合中的一个顶点相连接。在这里Vertex Cover问题是给定图 G 和点集的个数 g ，要找到图 G 的一个大小为 g 的点覆盖。（我们常说的最小顶点覆盖的问题称为顶点覆盖问题，毫无疑问，它也是一个NP-Complete问题）。
转化过程：
- 按照如下方法构造Graph，对应每一个变量 xi ，我们构造点二元点对 xi 和 x¯i ; 对于每一个clause，我们构造三角形的三个顶点，这3个点直接彼此有边，假设这三个点叫 A,B,C ，我们要建立 A,B,C 这三个点和该clause的联系：假设我们的clause是 (x1∨x¯2∨x¯3) 我们就把 x1 和 A 连起来， x¯2 和 B 连起来， x¯3 和 C 连起来。
- 下面的graph对应于 (x1∨x¯2∨x¯3)∧(x1∨x2∨x4) 。
- 若上图存在最小点覆盖，则将二元点对中在该最小点覆盖中的那一个赋值为1。则该赋值就是一个满足3-SAT的赋值。
假设有 m 个clause， n 个变量。则该规约过程建立了 3m+2n 个点， n+3m+3m 个边。显然可以在多项式时间完成该转换。
- 把P的输入转化到Q的输入：P的输入是包含 m 个clause的3SAT表达式；Q的输入当然是转化得到的图形 G 以及覆盖集的大小参数 g=2m+n 。
- 把Q的输出转化到P的输出：Q的输出是 G 的一个大小为 g=2m+n 的覆盖集；P的输出是3SAT的一个赋值。假设有图 G 的一个大小为 g=2m+n 的顶点覆盖，则其中必定包含所有二元点对中的一个点和三角形的两个顶点。对于每个clause对应的三角形的三个边必定被至少一个点覆盖，所以有一个可满足的真值赋值；对于每个二元点对，如果 xi 在 S 中，则 xi=1 ，如果 x¯i 在 S 中，则 xi=0 。
3. 3SAT <= ILP
- ILP就是Integer Linear Programming，即所有变量都要求是整数。
- 转化过程：
- 对于 每个clause，我们都对应于ILP中的一个constraint，比如 3SAT中有4个变量， x1 ， x2 ， x3 和 x4 ， 则ILP中也有同样的这4个变量，并且我们要求他们都是只能取0 或 1。对于一个clause，如 (x1∨x¯2∨x¯3) ，我们对应的constraint是 “ x1+（1−x2）+（1−x3）=1 。很显然了，ILP中的变量选0对应于3SAT中的变量选 0 ，ILP中的变量选1对应于3SAT中的变量选 1 .
- 3SAT问题 (x1∨x¯2∨x¯3)∧(x1∨x2∨x4) 对应的ILP如下：
{x1+（1−x2）+（1−x3）=1x1+x2+x4=1
- 至于input/output的转换，就如转换过程的描述，异常简单。在此不再叙述。
4. 3SAT <= Hamiltonian cycle problem
- 转化过程：
- 对每个变量 xi(1≤i≤n) ，创建 3m+3 个顶点，命名为 vi,1,vi,2,⋯,vi,3m+3 ，并且对相邻序号的两个顶点添加互相之间的有向边。如果 xi=1 ，则形成从左向右的一个路径；如果 x¯i=1 ，则形成从右向左的一个路径。
- 对每个 1≤i≤n−1 ，添加四条有向边 (vi,1,vi+1,1),(vi,3m+3,vi+1,3m+3),(vi,1,vi+1,3m+3),(vi,3m+3,vi+1,1) 。
- 添加两个节点 s,t ，添加有向边 (s,v1,1),(s,v1,3m+3),(vn,1,t),(vn,3m+3,t) 。然后再添加有向边 (t,s) 。这时得到的图中有 hamiltonian cycle，其中一个如下图的虚线所示。
- 对于每一个clause cj=z1z2z3 ，创建对应的顶点 cj 。如果 z=xi ，则添加有向边 (vi,3j,cj)和(cj,vi,3j+1) ; 如果 z=x¯i ，则添加有向边 (cj,vi,3j)和(vi,3j+1,cj) 。这里 1≤j≤m,1≤i≤n 。如对子句 c=x1∨x¯2∨x4 生成如下图中红色所示。如果选择子句中 x1=1 ，则 x1 对应的路径为从左向右；如果选择 x¯2=1 ，则 x2 对应的路径为从右到左；如果选择 x4=1 ，则 x4 对应的 路径为从左到右。这样我们就得到了最终的图 G 。
- 若图 G 有Hamiltonian cycle，则对每一个变量 xi 对应的路径都是单向的，若为从左到右，则 xi=1 ；若为从右到左，则 xi=0 。则该赋值肯定是3SAT可满足的。
- 该转化过程要创建 (3m+3)n+m+2 个点和 (3m+2)×2×n+4(n−1)+5+2m 个边，是多项式时间的。
- 把P的输入转化到Q的输入：P的输入是包含 m 个clause, n 个变量的的3SAT表达式；Q的输入当然是转化得到的包含 (3m+3)n+m+2 个点和 (3m+2)×2×n+4(n−1)+5+2m 个边的图形 G 。
- 把Q的输出转化到P的输出：Q的输出是 G 的一个Hamiltonian cycle；P的输出是3SAT的一个赋值。
5. Subset sum problem <= Partition problem
- 问题描述：
- Subset sum problem：given a set (or multiset) of integers T=(t1,t2,⋯,tn) , is there a non-empty subset whose sum is k 。
- Partition problem: partition problem (or number partitioning) is the task of deciding whether a given multiset W of positive integers can be partitioned into two subsets W1 and W2 such that the sum of the numbers in W1 equals the sum of the numbers in W2 .
转化过程：
- 给定一个子集和的实例为 T=(t1,t2,⋯,tn) ，数 k 。设 ∑t∈Tt=A ，则在 T 的基础上添加两个数 {2A−k,A+k} ，组成一个划分问题的实例 W ，即
W={T,2A−k,A+k}.则 ∑w∈Ww=4A 。
- 假设找到了 W 的一个划分 W1 和 W2 ，则有
∑w∈W1w=∑w∈W2w=2A。而且，新添加的两个元素肯定不会同时在 W1 或 W2 里，否则二者所在的子集的元素和必定大于二者之和 3A>2A 。 2A−k 所在的子集的其它元素就是一个满足子集和问题的子集。
- 给定一个子集和的实例为 T=(t1,t2,⋯,tn) ，数 k 。设 ∑t∈Tt=A ，则在 T 的基础上添加两个数 {2A−k,A+k} ，组成一个划分问题的实例 W ，即
把P的输入转化到Q的输入：P的输入是集合 T 以及数 k ；Q的输入是 W={T,2A−k,A+k}.
- 把Q的输出转化到P的输出：Q的输出是 W 的二划分 W1 和 W2 ，有 ∑w∈W1w=∑w∈W2w ；P的输出是 2A−k 所在的子集的其它元素集合。
6. Clique problem<=Subgraph isomorphism problem
- 问题描述
- Clique problem：给定一个图 G=(V,E) 和整数 k ，找到 G 的大小为 k 的团。
- Subgraph isomorphism problem：给定两个图 G1=(V1,E1),G2=(V2,E2) ，能否找到 G1 的一个子图 H ，使得 H 与 G2 同构。
- 转换过程：
- 令 G1=G ，构造 G2 为包含 k 个顶点的完全图（即团）。
- 如果子图同构问题的答案是肯定的，那么枚举 G 中的任意 k 个顶点并判定其是否是团，复杂度是多项式的 Ckn 。
- 把P的输入转化到Q的输入：P的输入是图 G=(V,E) 和整数 k ；Q的输入是 G1 和 G2 。
- 把Q的输出转化到P的输出：Q的输出是Yes/No；P的输出是 G 的一个团。
7. Partition problem <= Knapsack problem
- 问题描述：
- Partition problem： partition problem (or number partitioning) is the task of deciding whether a given multiset W of positive integers can be partitioned into two subsets W1 and W2 such that the sum of the numbers in W1 equals the sum of the numbers in W2 , i.e.
∑t∈W1t=∑t∈W2t=∑t∈Wt2.
- Knapsack problem：Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. 给定一个物品集合 U={u1,u2,⋯,un} ，且每个物品有大小 s(u) 和价值 w(u) ，正整数 B 和正数 K ，是否存在子集 U′⊂U 使得
∑u∈U′s(u)≤B,∑u∈U′w(u)≥K.
- Partition problem： partition problem (or number partitioning) is the task of deciding whether a given multiset W of positive integers can be partitioned into two subsets W1 and W2 such that the sum of the numbers in W1 equals the sum of the numbers in W2 , i.e.
- 转化过程：
- For each t∈W ，构造一个item u 且 s(u)=w(u)=t , 然后对 B,K 添加如下条件
B=K=∑u∈Uu2，那么有∑u∈U′s(u)=∑u∈U′w(u)=∑u∈Uu2。
- For each t∈W ，构造一个item u 且 s(u)=w(u)=t , 然后对 B,K 添加如下条件
8. Vertex Cover <=Independent Set
- 问题描述：
- Vertex Cover：给定一个图 G=(V,E) 和整数 k ，找到 G 的大小为 k 的点覆盖。
- Independent Set：给定一个图 G=(V,E) 和整数 k ， 找到 G 的大小为 k 的独立集。
- 转化过程：
- 把参数为 G=(V,E) 和整数 k 的点覆盖问题转化为参数为 G=(V,E) 和整数 |V|−k 的独立集问题。
- 若 G 中有 |V|−k 大小的独立集 S′ ，则 G 中的任意一条边的两端点不可能都在 S′ 里。也就是说， G 的任意一条边至少与该独立集 S′ 之外的其余 k 个顶点的某一个关联，即该独立集 S′ 之外的其余 k 个顶点是 G 的一个大小为 k 的点覆盖。
- 把P的输入转化到Q的输入：P的输入是图 G=(V,E) 和整数 k ；Q的输入是图 G=(V,E) 和整数 |V|−k ；
- 把Q的输出转化到P的输出：Q的输出是 G 的 |V|−k 大小的独立集 S′ ，P的输出是 V−S′ .
9. Independent Set <= Clique problem
- 问题描述：
- Independent Set：给定一个图 G=(V,E) 和整数 k ， 找到 G 的大小为 k 的独立集。
- Clique problem：给定一个图 G=(V,E) 和整数 k ，找到 G 的大小为 k 的团。
- 转化过程：
- 把 G 的大小为 k 的独立集问题转化为补图 G¯ 的大小为 k 的团问题。
- 如果找到补图 G¯ 的大小为 k 的团，则该团内的任意两个顶点在原图 G 中没有连接边，即该团的 k 个顶点是原图 G 的大小为 k 的独立集。
- 把P的输入转化到Q的输入：P的输入是图 G=(V,E) 和整数 k ；Q的输入是补图 G¯ 和整数 k ；
- 把Q的输出转化到P的输出：Q的输出是补图 G¯ 的 k 大小的独立集 S′ ，P的输出是 V−S′ .
10. Hamiltonian cycle problem <= Hamiltonian path problem
- 问题描述：
- Hamiltonian cycle problem：a graph cycle (i.e., closed loop) through a graph that visits each node exactly once
- Hamiltonian path problem： a graph path between two vertices of a graph that visits each vertex exactly once.
- 转化过程：
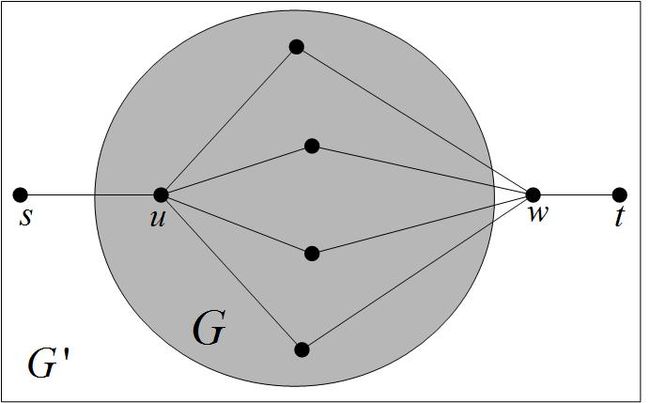
- 在原图 G 基础上再添加 s,w,t 三个顶点，任选 G 中一点 u ，连接 (s,u),(w,t) 以及连接 u 的所有相邻节点与 w ，生成新图 G′ 。如上图所示。
- 假设新图 G′ 有一个Hamiltonian path <s,u,v1,v2,⋯,v,w,t> ，由于 u,v 为相邻节点，故 <u,v1,v2,⋯,v> 为 G 的Hamiltonian cycle。
11. Hamiltonian cycle problem <= Traveling salesman problem
- 问题描述：
- Hamiltonian cycle problem：a graph cycle (i.e., closed loop) through a graph G=(V,E) that visits each node exactly once。
- Traveling salesman problem： 即给定一个带权图 G′=(V′,E′) 和数 k ，找到一个费用为 k 的回路。
- 转化过程：如何得到 G′=(V′,E′) 和数 k
- V’=V，k=0..
- E’为完全图的边。还要定义边的权重：
w(u,v)={0,if(u,v)∈E1,if(u,v)∉E
- 如果 G′=(V′,E′) 有个费用为 k=0 的回路，则说明这些边都是在 G 中存在的，因此是 G 的一个Hamiltonian cycle problem。
参考资料
- 关于P，NP，NPC等问题
- http://blog.csdn.net/wwy851/article/details/6082007
- http://blog.csdn.net/wwy851/article/details/6082025
- 澄清P问题、NP问题、NPC问题的概念
http://www.matrix67.com/blog/archives/105 - 完備 (複雜度)
http://zh.wikipedia.org/wiki/%E5%AE%8C%E5%82%99_(%E8%A4%87%E9%9B%9C%E5%BA%A6) - P/NP/NPC/NP-hard
http://ccckmit.github.io/ct/htm/book.html - Cook-Levin理論
http://zh.wikipedia.org/wiki/Cook-Levin%E7%90%86%E8%AB%96
提到了两篇论文 - A Sample Proof of NP-Completeness
http://cgm.cs.mcgill.ca/~athens/cs507/Projects/2001/CW/npproof.html - 算法导论自学笔记
http://blog.csdn.net/xiazdong/article/category/1270511 - Reductions & NP-completeness
https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/npcomplete.pdf - Reductions Between NPCs
http://mlnotes.com/2013/04/29/npc.html - Lecture Notes on Complexity and NP-completeness 1. Reduc
http://www.cs.berkeley.edu/~vazirani/s99cs170/notes/npc.pdf - Reductions Between NPCs
http://mlnotes.com/2013/04/29/npc.html - Everyday encounters with NP-complete problems
http://cstheory.stackexchange.com/questions/446/everyday-encounters-with-np-complete-problems - NP-hardness of an optimization problem
http://cstheory.stackexchange.com/questions/14787/np-hardness-of-an-optimization-problem?rq=1 - Is the following optimization problem NP-hard?
http://cstheory.stackexchange.com/questions/10615/is-the-following-optimization-problem-np-hard - Is the following optimization problem (a variant to a previous problem) NP-hard?
http://cstheory.stackexchange.com/questions/10727/is-the-following-optimization-problem-a-variant-to-a-previous-problem-np-hard?rq=1 - What are NP-complete problems and why are they so important?
http://math.stackexchange.com/questions/726/what-are-np-complete-problems-and-why-are-they-so-important