Google 机器学习编程笔记八——分类理论基础

基础概念：

1、分类阈值

逻辑回归返回的是概率。 您可以“原样”使用返回的概率（例如，用户点击此广告的概率为 0.00023），也可以将返回的概率转换成二元值（例如，这封电子邮件是垃圾邮件）。

如果某个逻辑回归模型对某封电子邮件进行预测时返回的概率为 0.9995，则表示该模型预测这封邮件非常可能是垃圾邮件。相反，在同一个逻辑回归模型中预测分数为 0.0003 的另一封电子邮件很可能不是垃圾邮件。可如果某封电子邮件的预测分数为 0.6 呢？

为了将逻辑回归值映射到二元类别，您必须指定分类阈值（也称为判定阈值）。

如果值高于该阈值，则表示“垃圾邮件”；如果值低于该阈值，则表示“非垃圾邮件”。人们往往会认为分类阈值应始终为 0.5，但阈值取决于具体问题，因此您必须对其进行调整。

注意：“调整”逻辑回归的阈值不同于调整学习速率等超参数。在选择阈值时，需要评估您将因犯错而承担多大的后果。

2、正分类与负分类

假设“狼来了”故事中，我们做出以下定义（注意此定义是一个相对概念）：

• “狼来了”是正类别。
• “没有狼”是负类别。

我们可以使用一个 2x2 混淆矩阵来总结我们的“狼预测”模型，该矩阵描述了所有可能出现的结果（共四种）：

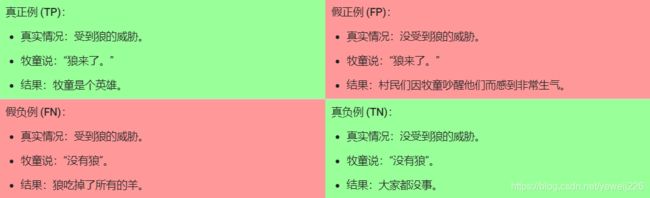
真正例是指模型将正类别样本正确地预测为正类别。同样，真负例是指模型将负类别样本正确地预测为负类别。

假正例是指模型将负类别样本错误地预测为正类别，而假负例是指模型将正类别样本错误地预测为负类别。

3、准确率（预测正确率）

准确率是一个用于评估分类模型的指标。通俗来说，准确率是指我们的模型预测正确的结果所占的比例。正式点说，准确率的定义如下：

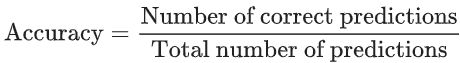
对于二元分类，也可以根据正类别和负类别按如下方式计算准确率：

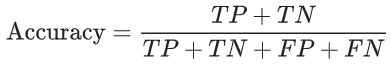
其中，TP = 真正例，TN = 真负例，FP = 假正例，FN = 假负例。

让我们来试着计算一下以下模型的准确率，该模型将 100 个肿瘤分为恶性 （正类别）或良性（负类别）：

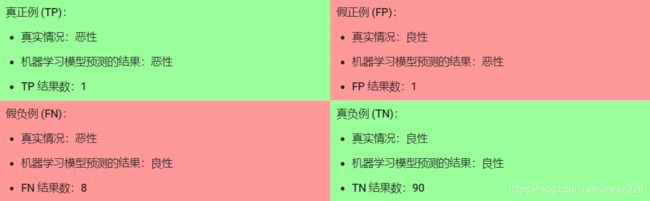
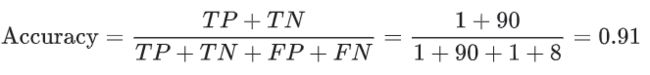
准确率为 0.91，即 91%（总共 100 个样本中有 91 个预测正确）。这表示我们的肿瘤分类器在识别恶性肿瘤方面表现得非常出色；但实际上，只要我们仔细分析一下正类别和负类别，就可以更好地了解我们模型的效果。

在 100 个肿瘤样本中，91 个为良性（90 个 TN 和 1 个 FP），9 个为恶性（1 个 TP 和 8 个 FN）。

在 91 个良性肿瘤中，该模型将 90 个正确识别为良性。这很好。不过，在 9 个恶性肿瘤中，该模型仅将 1 个正确识别为恶性。这是多么可怕的结果！9 个恶性肿瘤中有 8 个未被诊断出来！

当您使用分类不平衡的数据集（比如正类别标签和负类别标签的数量之间存在明显差异）时，单单准确率一项并不能反映全面情况。

4、精确率与召回率

精确率指标尝试回答在被识别为正类别的样本中，确实为正类别的比例是多少？

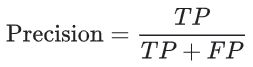
如果模型的预测结果中没有假正例，则模型的精确率为 1.0。
如下例中


该模型的精确率为 0.5，也就是说，该模型在预测恶性肿瘤方面的正确率是 50%。

召回率尝试回答在所有正类别样本中，被正确识别为正类别的比例是多少？

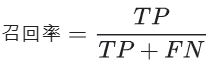
例如


该模型的召回率是 0.11，也就是说，该模型能够正确识别出所有恶性肿瘤的百分比是 11%。

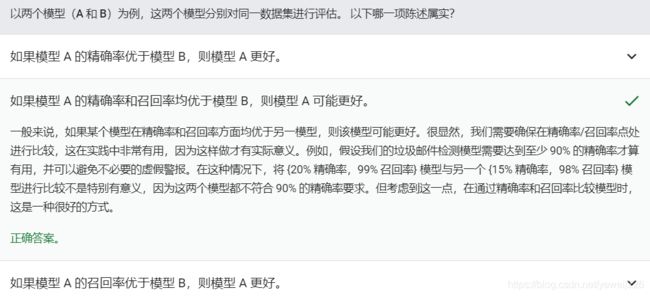
要全面评估模型的有效性，必须同时检查精确率和召回率。遗憾的是，精确率和召回率往往是此消彼长的情况。 也就是说，提高精确率通常会降低召回率值，反之亦然。

请观察下图来了解这一概念，该图显示了电子邮件分类模型做出的 30 项预测。分类阈值右侧的被归类为“垃圾邮件”，左侧的则被归类为“非垃圾邮件”。

根据图中可得

精确率指的是被标记为垃圾邮件的电子邮件中正确分类的电子邮件所占的百分比，即图中阈值线右侧的绿点所占的百分比：

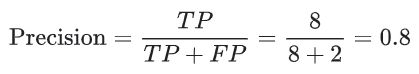
召回率指的是实际垃圾邮件中正确分类的电子邮件所占的百分比，即图中阈值线右侧的绿点所占的百分比：

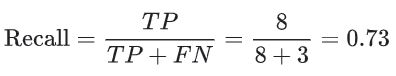
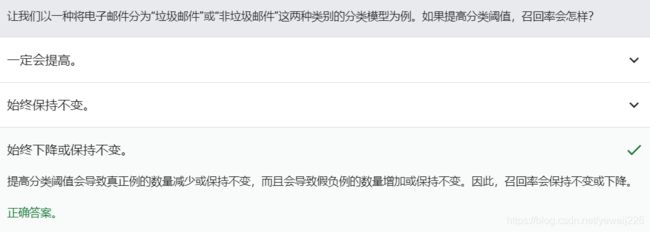
如果提高分类阈值

假正例数量会减少，但假负例数量会相应地增加。

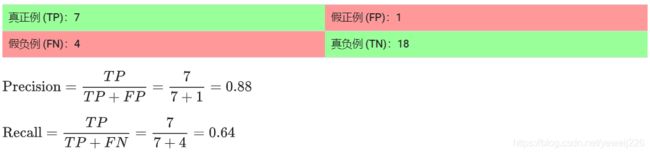
结果，精确率有所提高，而召回率则有所降低：

若降低分类阈值，则会获得相反的效果


检测理解程度：

准确率需要根据实际情况理解，看高准确率模型若错误产生的后果是否严重

5、ROC曲线和曲线下面积

ROC 曲线（接收者操作特征曲线） 是一种显示分类模型在所有分类阈值下的效果的图表。该曲线绘制了真正例率与假正例率两个参数

真正例率 (TPR) 是召回率的同义词，因此定义如下：

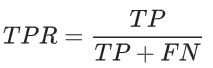
假正例率 (FPR) 的定义如下：

仔细看这两个公式，发现其实TPRate就是TP除以TP所在的列，FPRate就是FP除以FP所在的列，二者意义如下：

TPRate的意义是所有真实类别为1的样本中，预测类别为1的比例。
FPRate的意义是所有真实类别为0的样本中，预测类别为1的比例。

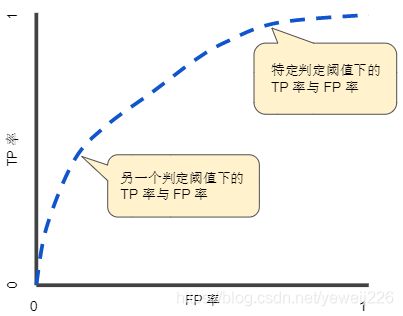
ROC 曲线用于绘制采用不同分类阈值时的 TPR 与 FPR。

降低分类阈值会导致将更多样本归为正类别，从而增加假正例和真正例的个数。下图显示了一个典型的 ROC 曲线。

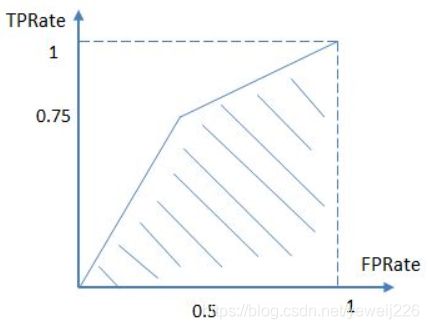
按照定义，AUC即ROC曲线下的面积，而ROC曲线的横轴是FPRate，纵轴是TPRate，当二者相等时，即y=x，如下图:

表示的意义是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的。换句话说，分类器对于正例和负例毫无区分能力，和抛硬币没什么区别，一个抛硬币的分类器是我们能想象的最差的情况，因此一般来说我们认为AUC的最小值为0.5（当然也存在预测相反这种极端的情况，AUC小于0.5，这种情况相当于分类器总是把对的说成错的，错的认为是对的，那么只要把预测类别取反，便得到了一个AUC大于0.5的分类器）。

而我们希望分类器达到的效果是：对于真实类别为1的样本，分类器预测为1的概率（即TPRate），要大于真实类别为0而预测类别为1的概率（即FPRate），即y＞x，因此大部分的ROC曲线长成下面这个样子：

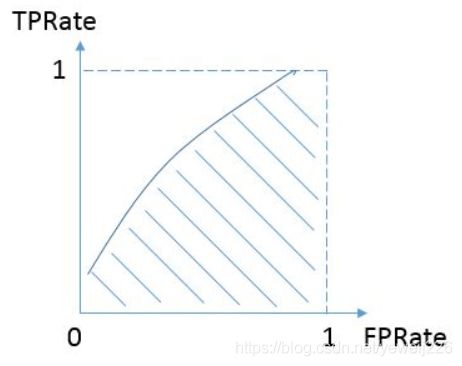
最理想的情况下，没有真实类别为1而错分为0的样本，TPRate一直为1，于是AUC为1，这便是AUC的极大值。

例如：

得到混淆矩阵如下：

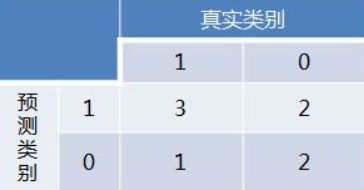
进而算得TPRate=3/4，FPRate=2/4，得到ROC曲线：

最终得到AUC为0.625。

如果预测结果是逻辑概率，如：

这时，需要设置分类阈值来得到混淆矩阵，不同的阈值会影响得到的TPRate，FPRate，如果阈值取0.5，小于0.5的为0，否则为1，那么我们就得到了与之前一样的混淆矩阵。其他的阈值就不再啰嗦了。

依次使用所有预测值作为阈值，得到一系列TPRate，FPRate，描点，求面积，即可得到AUC。

最后说说AUC的优势，AUC的计算方法同时考虑了分类器对于正例和负例的分类能力，在样本不平衡的情况下，依然能够对分类器作出合理的评价。

例如在反欺诈场景，设欺诈类样本为正例，正例占比很少（假设0.1%），如果使用准确率评估，把所有的样本预测为负例，便可以获得99.9%的准确率。但是如果使用AUC，把所有样本预测为负例，TPRate和FPRate同时为0（没有Positive），与(0,0) (1,1)连接，得出AUC仅为0.5，成功规避了样本不均匀带来的问题。水平有限，欢迎拍砖~

（ROC与AUC内容出自知乎）

6、预测偏差

逻辑回归预测应当无偏差。即：“预测平均值”应当约等于“观察平均值”

预测偏差指的是这两个平均值之间的差值。即：
预测偏差 = 预测平均值 - 数据集中相应标签的平均值

如果出现非常高的非零预测偏差，则说明模型某处存在错误，因为这表明模型对正类别标签的出现频率预测有误。

例如，假设我们知道，所有电子邮件中平均有 1% 的邮件是垃圾邮件。如果我们对某一封给定电子邮件一无所知，则预测它是垃圾邮件的可能性为 1%。同样，一个出色的垃圾邮件模型应该预测到电子邮件平均有 1% 的可能性是垃圾邮件。（换言之，如果我们计算单个电子邮件是垃圾邮件的预测可能性的平均值，则结果应该是 1%。）然而，如果该模型预测电子邮件是垃圾邮件的平均可能性为 20%，那么我们可以得出结论，该模型出现了预测偏差。

造成预测偏差的可能原因包括：

• 特征集不完整
• 数据集混乱
• 模型实现流水线中有错误？
• 训练样本有偏差
• 正则化过强

您可能会通过对学习模型进行后期处理来纠正预测偏差，即通过添加校准层来调整模型的输出，从而减小预测偏差。

逻辑回归可预测 0 到 1 之间的值。不过，所有带标签样本都正好是 0（例如，0 表示“非垃圾邮件”）或 1（例如，1 表示“垃圾邮件”）。因此，在检查预测偏差时，您无法仅根据一个样本准确地确定预测偏差；您必须在“一大桶”样本中检查预测偏差。也就是说，只有将足够的样本组合在一起以便能够比较预测值（例如 0.392）与观察值（例如 0.394），逻辑回归的预测偏差才有意义。

您可以通过以下方式构建桶：

• 以线性方式分解目标预测。
• 构建分位数。

请查看以下某个特定模型的校准曲线。每个点表示包含 1000 个值的分桶。两个轴具有以下含义：

• x 轴表示模型针对该桶预测的平均值。
• y 轴表示该桶的数据集中的实际平均值。

两个轴均采用对数尺度。

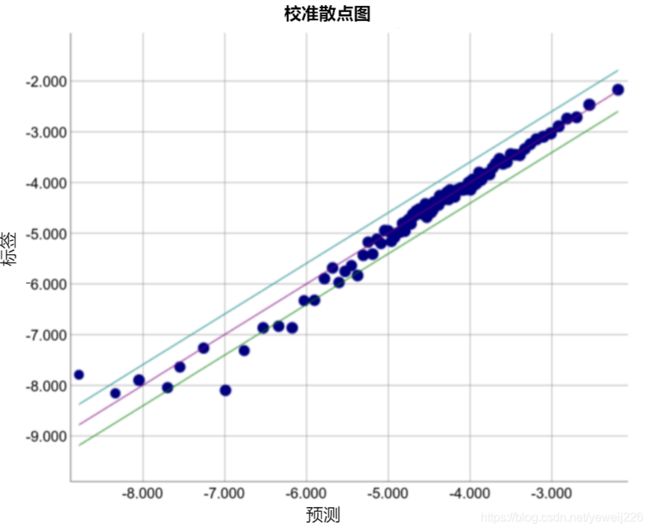
为什么只有模型的某些部分所做的预测如此糟糕？以下是几种可能性：

• 训练集不能充分表示数据空间的某些子集。
• 数据集的某些子集比其他子集更混乱。
• 该模型过于正则化。（不妨减小 lambda 的值。）