跑步爱天天(欧拉序)
【问题描述】
YOUSIKI 在 noip2016 的一道《天天爱跑步》的题爆零后,潜心研究树上问题,成为了一代大师,于是皮皮妖为了测验他,出了一道题,名曰《跑步爱天天》。
有一个以1为根的有根树,初始每个点都有个警卫,每个警卫会按深度优先的顺序周期性的巡逻以其初始点为根的子树(详见样例解释),一个时刻走且仅走一条边。
YOUSIKI 初始在x点,他要到根结点拜访皮皮妖,他会沿着最短路径走,一个时刻走且仅走一条边,当他走到这个点时,如果遇到了警卫,他会消耗1点妖气将这个警卫杀死,杀死后的警卫就不会在以后的路程中出现。
那么 YOUSIKI 需要消耗几点妖气才能拜访到皮皮妖呢?
【输入格式】
第一行一个数字 T,表示有 T 组数据。
对于每组数据,第一行一个整数 n,表示树有 n 个结点。
接下来 n 行,第 i 行有一个整数 k,表示 i 号点儿子个数,接下来 k 个整数,表示 k 个有序儿子 (“有序” 的含义详见样例解释)。
最后一行一个整数 x,表示 YOUSIKI 的出发点。
【输出格式】
输出 T行,每行一个整数表示答案。
【样例输入1】
1
6
2 2 3
2 4 5
1 6
0
0
0
6
【样例输出1】
1
【样例解释】
为了方便,我们把初始在i号点的警卫称为警卫i。
警卫1的一个周期内的巡逻路线为:1->2->4->2->5->2->1->3->6->3->1。
警卫2的一个周期内的巡逻路线为:2->4->2->5->2。
警卫3的一个周期内的巡逻路线为:3->6->3。
警卫4,5,6一直不动。
YOUSIKI 的路线为:6->3->1。
YOUSIKI 初始在6号点,需要杀掉警卫6。第一时刻他在3号点,虽然他和警卫3对穿过去,但是由于没有在点上相遇,所以不算相遇。第二时刻他在1号点,此时1号点没有警卫。
注意
警卫的巡逻是周期性的,例如,初始在2号点警卫的巡逻路线为:2->4->2->5->2->4->2->5->2->4->2->5->2->...
输入格式中的 “有序” 指的是比如1号点的儿子先输入的2再输入的3,那么1号点巡逻时就要先巡逻2再巡逻3。
本题输入文件较大,可以使用快速输入输出
【数据范围与约定】
对于20%的数据,n≤100。
对于40%的数据:n≤2000。
对于另外10%的数据:树高≤5。
对于另外10%的数据:树是一条链。
对于100% 的数据:T≤10,n≤500000。
首先这题数据很奇怪,我最开始用了一种完全错误的想法居然可以得80分。
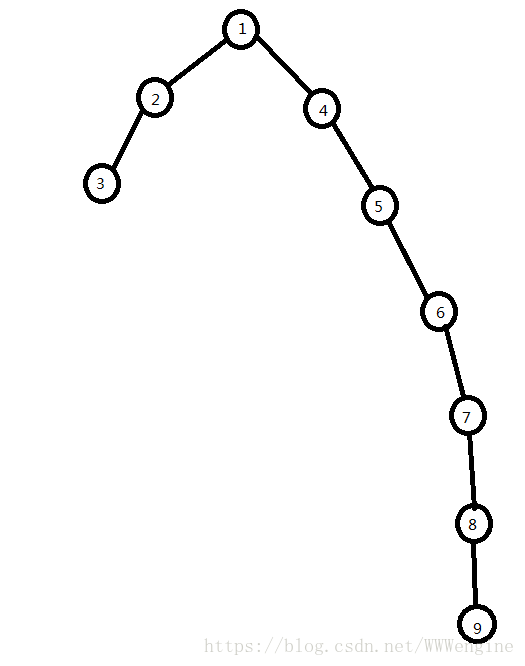
我最初的想法是:一遍DFS到底,一旦发现到达S就返回一个距离dis,并且每个节点i只记录S所在子树的左边子树的大小。设i节点的警卫在左边的子树里用了tmp的时间,我们枚举i的子树,每次tmp加上枚举到的子树大小的两倍(来回),直到第一次tmp大于等于dis时或者枚举到S所在子树时break掉,看dis-tmp能否被2整除,能则答案加一。大概是这个图:
假定S从9出发,讨论的是1处的警卫。1处警卫回到1时走了4步,S也走4步到达5,此时两者相距2,可以遇见。
可实际上情况很有可能是这样的:
也就是说,1的警卫还有可能先走4,5,...的左边子树再与S相遇,而这是无法在时间限制内计算的。如此简单的情况能忽略我可能是傻掉了(居然有80pts)...
***下面正解是看的题解。
欧拉序就是指每遍历到一个节点就把它加入队列末尾,不论是第一次访问还是递归回来(抄的)。样例手打一下草稿,一次DFS过后形成的序列,可以发现有的节点多次出现,并且这些节点的警卫只在节点第一次出现和最后一次出现这段之间走来走去。
思考一下可以发现,一个节点的父、祖节点,在这个序列里第一次出现的位置,与它第一次出现位置的间隔,就是父、祖节点到它需要走的步数。
再来看这题,S每到一个节点i可以得到目前所用的时间Time,思考哪个父、祖节点可以用Time的时间到i?当然是在欧拉序上与i距离Time的父祖。可以想到不会有父祖在一个点重合。另外,由于警卫一旦和S对穿过去就不会再追到S,所以要求父祖节点是第一次在这个序列里出现,且只统计一次。
代码有注释
#include
using namespace std;
const int MAXN=500005;
int N,S,np,tot,Clock,last[MAXN],dep[MAXN],dfn[MAXN*10];
int mark[MAXN],V[MAXN],Time[MAXN],fa_first[MAXN*10],vis[MAXN];
struct edge{int to,pre;}E[MAXN];
char c;
void scan(int &x)
{
for(c=getchar();c<'0'||c>'9';c=getchar());
for(x=0;c>='0'&&c<='9';c=getchar()) x=x*10+c-'0';
}
void addedge(int u,int v)
{
E[++np]=(edge){v,last[u]};
last[u]=np;
}
void init()
{
memset(last,0,sizeof(last));
memset(mark,0,sizeof(mark));
memset(vis,0,sizeof(vis));
memset(vis,0,sizeof(vis));
np=0; tot=0; Clock=0;
}
void dfs(int i)
{
dfn[++tot]=i; fa_first[tot]=1; //加入序列,第一次出现打标记
if(S==i) mark[i]=1; //把S的路径标记
for(int p=last[i];p;p=E[p].pre)
{
int j=E[p].to;
dep[j]=dep[i]+1;
dfs(j);
if(mark[j]) mark[i]=1; //S所在路径
dfn[++tot]=i; fa_first[tot]=0; //i不是第一次出现,标记打为0
}
if(mark[i]) Time[i]=Clock++; //如果在路径上,记录所用时间
}
int main()
{
int T,i,u,v;
scan(T);
while(T--)
{
init();
scan(N);
for(u=1;u<=N;u++)
{
scan(i);
for(int k=1;k<=i;k++) scan(V[k]); //有序
for(int k=i;k>=1;k--) addedge(u,V[k]);
}
scan(S);
dep[1]=1;
dfs(1);
int ans=0;
for(i=1;i<=tot;i++)
{
u=dfn[i];
if(mark[u]&&i-Time[u]>0&&fa_first[i-Time[u]])
{ //u在S的路径上,且距u为Time的节点是第一次出现。中间的判断是防止负数
v=dfn[i-Time[u]];
if(mark[v]&&dep[v]<=dep[u]&&!vis[v])
{ //v在S的路径上 且是u的父祖 且没有计算过
ans++;
vis[v]=1;
}
}
}
cout<