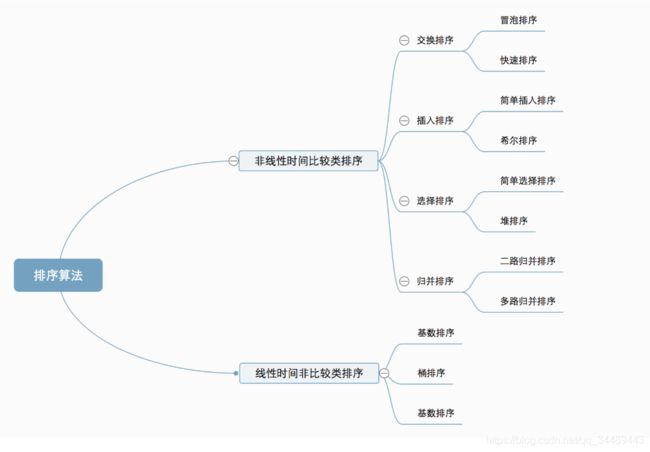
排序算法
注意:以下所有的排序都是按照递增的顺序排序
参考链接:https://www.cnblogs.com/fnlingnzb-learner/p/9374732.html
文章目录
-
-
-
- 1、选择排序
- 2、冒泡排序
- 3、插入排序
- 4、希尔排序
- 5、归并排序
- 6、快速排序
- 7、堆排序
- 8、桶排序
- 9、计数排序
- 10、基数排序
- 11、总结
-
-
1、选择排序
选择排序很简单,就是先遍历数组中的Size个元素,找到最小值放在第一位,然后在遍历数组中后Size-1个元素,找到最小值放在第二位,一次类推。
时间复杂度:O(n*n),空间复杂度:O(1),不稳定(举例说明:序列5,8,5,3,9,第一次会将第一个5和3互换位置,这样两个5的相对位置就改变了)
void SelectSort(vector<int>& nums) {
int Size = (int)nums.size();
for (int i = 0; i < Size - 1; ++i)
{
int Min = i;
for (int j = i + 1; j < Size; ++j)
Min = nums[Min] > nums[j] ? j : Min;
swap(nums[i], nums[Min]);
}
}
2、冒泡排序
冒泡排序就是每一次比较两个相邻的元素的大小,如果不是递增顺序,就调换位置。其实整个过程是和选择排序相反的过程,每一次大循环,找到未排序元素中最大的元素,放置到最后。
时间复杂度:O(n*n),空间复杂度:O(1),稳定
void BubbleSort(vector<int>& nums) {
int Size = (int)nums.size();
for (int i = 0; i < Size; ++i)
//每循环一次,都可以找到前Size - i个元素中最大的元素,并放到nums[Size - i - 1]的位置上
{
for (int j = 0; j < Size - 1 - i; ++j)
if (nums[j] > nums[j + 1])
swap(nums[j], nums[j + 1]);
}
}
3、插入排序
可以理解为前若干个元素是已经排好序的,将当前元素插入到前面若干个元素中,组成一个新的数组。
时间复杂度:O(n)~O(n*n),空间复杂度:O(1),稳定
时间复杂度随着数组有序性越好,复杂度越低。
void InsertSort(vector<int>& nums) {
int Size = (int)nums.size();
for (int i = 1; i < Size; ++i)
//每次认为前i个元素是排好序的子数组,然后将第i个元素插入到前i个元素中,也就是比他大的就交换元素位置
{
for (int j = i; j >= 1 && nums[j] < nums[j - 1]; --j)
swap(nums[j], nums[j - 1]);
}
}
4、希尔排序
希尔排序其实是优化版的插入排序,主要思想就是将输入数组用gap(增量)划分成若干个子数组,也就是0,gap,2×gap…是一组,1,gap+1,2×gap + 1…是一组,以此类推。然后将gap增加,最后子数组就合并成一个数组了。具体可以参考这篇文章,写的通俗易懂:https://blog.csdn.net/qq_39207948/article/details/80006224
插入排序之所以可以进行优化,是因为插入排序有这样一个特性,就是时间复杂度在n~n×n之间,如果数组排序性越好,那么时间复杂度越低。所以先将数组划分成小数组,这样即使是n×n复杂度,也不会很大,因为数组个数少(也就是n小)。然后不断合并,最后大数组的排序性比较好了,所以时间复杂度也就降低了。
时间复杂度:O(n)~O(n×n),空间复杂度:O(1),不稳定(举例说明:序列7,5,5,8在第一次循环时,7和第二个5换位,就改变了两个5的相对顺序)
//这样写更容易理解,其实最快的只用一个函数来写
void InsertSort(vector<int>& nums, int gap, int index)
{
for (int i = index; i - gap >= 0 && nums[i] < nums[i - gap]; i -= gap)
swap(nums[i], nums[i - gap]);
}
void ShellSort(vector<int>& nums) {
int Size = (int)nums.size();
for (int gap = Size / 2; gap >= 1; gap /= 2)
for (int i = gap; i < Size; ++i)
{
InsertSort(nums, gap, i);
}
}
5、归并排序
归并排序就是先分成小数组,再排序,所以需要记住的是主要函数Merge中是先分,再排序,这个递归需要记住。我自己想到在排序的步骤中可以用插入排序的方法,空间复杂度明显降低,但是时间复杂度不稳定。
时间复杂度:O(nlog2n),空间复杂度:O(n),稳定
void Sort(vector<int>& nums, int start, int middle, int end)
{
//插入排序方法,空间复杂度为1,但是时间复杂度不稳定
/*for (int i = middle + 1; i <= end; ++i)
for (int j = i - 1; j >= start && nums[j + 1] < nums[j]; --j)
swap(nums[j + 1], nums[j]);*/
//一般的归并排序的方法,时间复杂度稳定
vector<int> v1;
vector<int> v2;
for (int i = start; i <= middle; ++i)
v1.push_back(nums[i]);
for (int i = middle + 1; i <= end; ++i)
v2.push_back(nums[i]);
v1.push_back(INT_MAX);
v2.push_back(INT_MAX);
int m = 0, n = 0;
for (int i = start; i <= end; ++i)
{
if (v1[m] > v2[n])
nums[i] = v2[n++];
else nums[i] = v1[m++];
}
}
void Merge(vector<int>& nums, int start, int end)
{
if (start < end)
{
int middle = start + (end - start) / 2;
Merge(nums, start, middle);
Merge(nums, middle + 1, end);
Sort(nums, start, middle, end);
}
}
void MergeSort(vector<int>& nums)
{
int Size = nums.size();
Merge(nums, 0, Size - 1);
}
6、快速排序
快速排序和归并排序是反的,归并排序是先分,然后再排序,快速排序是先按照中间那个数,将数组分成前后两个数组,相当于先排序,再分。
时间复杂度:O(nlog2n)~O(n×n),空间复杂度:O(1)
int Sort(vector<int>& nums, int start, int end, int val)
{
int j = start;
for (int i = start + 1; i <= end; ++i)
if (nums[i] < val)
{
j++;
swap(nums[i], nums[j]);//这里用了swap避免多余的空间占用
}
swap(nums[start], nums[j]);//这里是将中间值nums[start]放到两个子数组的中间。
return j;
}
void Merge(vector<int>& nums, int start, int end)
{
if (start < end)
{
int val = nums[start];//这里做了简化,每次用来划分子数组的值选取start那个,为了方便后面的划分
int middle = Sort(nums, start, end, val);
Merge(nums, start, middle - 1);
Merge(nums, middle + 1, end);
}
}
void FastSort(vector<int>& nums)
{
int Size = nums.size();
Merge(nums, 0, Size - 1);
}
快排的变种:
①当快排分割到尺寸较小的子数组时,使用插入排序更快,在STL中的排序就是这样优化的。
②三数取中,在快排中,时间复杂度主要取决于选取的切分值是否合适,这个值如果是较大或者较小值,那么切分得到的两个子数组会形成一个较大,一个较小的尺寸,不利于后续分割。所以如果切分值选取中位数是最好的,但是这样比较困难,所以可以在数组中选取三个值,比如开头,中间和末尾,比较选取这三个数中中间的那个值作为切分值,更合理。
③三向切分,当数组中有大量重复元素时,可以使用这种优化,就是将一个数组分成三个,小于切分值,等于切分值,大于切分值这三种情况来看。
代码如下:
pair<int, int> Sort(vector<int>& nums, int start, int end, int val)
{
//j可以理解为0~j-1都是小于val的,k+1~end都是大于val的
int j = start, i = start + 1, k = end;
while (i <= k)
if (nums[i] < val)//小于切分值的放左边
{
swap(nums[i++], nums[j++]);
}
else if (nums[i] > val)//大于切分值的放右边
{
swap(nums[i], nums[k--]);
}
else i++;//等于的不动
return pair<int, int>(j, k);
}
void Merge(vector<int>& nums, int start, int end)
{
if (start < end)
{
int val = nums[start];//这里做了简化,每次用来划分子数组的值选取start那个,为了方便后面的划分
pair<int, int> middle = Sort(nums, start, end, val);
Merge(nums, start, middle.first - 1);
Merge(nums, middle.second + 1, end);
}
}
void FastSort(vector<int>& nums)
{
int Size = nums.size();
Merge(nums, 0, Size - 1);
}
④可以用stl自带的partition函数来写快排,但是是差不多的。
7、堆排序
如果想要升序排列,就建立最大堆,然后将堆顶的元素放到数组最后,不断减小堆的尺寸。
其实整个堆排序的过程是将原数组就看成一个二叉树,然后不断使用调整堆结构的函数,使得这个二叉树具有最大堆的性质
时间复杂度:O(NlogN),空间复杂度:O(1),不稳定。
void AdjustHeap(vector<int>& nums, int index, int Size)//调整堆的结构,将下标为index的元素放到堆中合理的位置
{
int lchild = index * 2 + 1;
while (lchild < Size)
{
//找到子节点中较大的那个
if (lchild + 1 < Size && nums[lchild] < nums[lchild + 1])
++lchild;
//将子节点和父节点比较,如果子节点较大,就和父节点互换位置
if (nums[lchild] <= nums[index]) break;
else {
swap(nums[lchild], nums[index]);
index = lchild;
lchild = index * 2 + 1;
}
}
}
void MakeHeap(vector<int>& nums, int Size)
{
//注意这里的起始位置是(Size - 2) / 2,这里代表最后一个元素(Size - 1)的父节点是
//((Size - 1) - 1) / 2,所以起始位置就是这个
for (int i = (Size - 2) / 2; i >= 0; --i)
AdjustHeap(nums, i, Size);
}
void HeapSort(vector<int>& nums)//堆排序就是每次构建一个最大堆,然后将最大堆的堆顶元素放到堆的最后一个元素,然后堆尺寸减1,继续构建最大堆。
{
int Size = nums.size();
MakeHeap(nums, Size);
for (int i = Size - 1; i > 0; --i)
{
swap(nums[i], nums[0]);
MakeHeap(nums, i);
}
}
8、桶排序
桶排序就是用哈希表来排序,比如如下就是10以内不重复的同排序简单写法:
void TongSort(int *score,int num)
{
int a[11];
for(int i=0;i<=10;i++)
a[i]=0;
for(int i=0;i<num;i++)
{
int temp=score[i];
++a[temp];
}
for(int i=0;i<11;i++)
{
int num_print=a[i];
for(int j=1;j<=num_print;j++)
cout<<i<<" ";
}
}
9、计数排序
这种方法我觉得和桶排序差不多,我在桶排序中的例子也算是基数排序的例子,就是用一个足够大的数组,将元素作为数组的下标,但是桶排序可以有更复杂的表示方法,所以基数排序更简单。
10、基数排序
就是只用一个大小为10的数组,从各位,十位,百位的顺序开始遍历.如图所示:

代码如下:
/*
*求数据的最大位数,决定循环的次数
*/
int maxbit(vector<int> data)
{
int Size = data.size();
int bit = 1, div = 10;
for (int i = 0; i < Size - 1; ++i)
{
while (data[i] > div)
{
bit++;
div *= 10;
}
}
return div;
}
void radixsort(vector<int> &arr){
const int buckets_number = 10;
vector<vector<int> > buckets(10);//10个桶,每个桶是vector