旅游景区管理系统（二 ）搜索最短路径（MFC实现）

旅游景区管理系统

1.旅游景区导航
2.搜索最短路径
3.prim铺设电路
4.代码介绍和展示

搜索最短路径

本系列为武汉某大学课设，只是学习之用

功能要求：

输入：
① 起始景点的编号
② 终点的编号。
处理：使用迪杰斯特拉(Dijkstra)算法，求得从起始景点到终点之间的最短路径，计算路径总长度。
输出：
① 最短路线
② 路径总长度

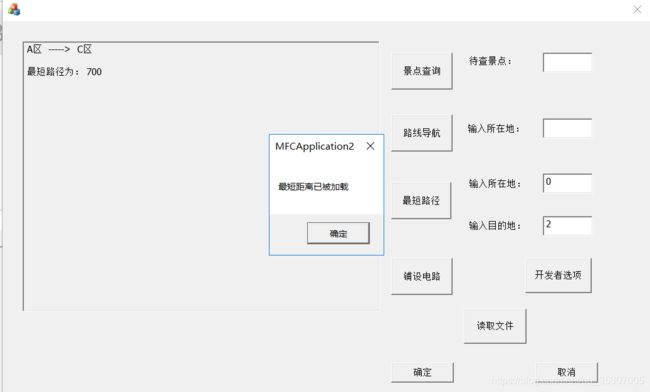
例子

代码块展示

//dijstra求最短路径
void CMFCApplication2Dlg::OnBnClickedButton3()
{
	CString Information;										//显示屏幕操作
	CString X("最短路径为： "), Y("\r\n"), Z("  ----->  ");
	CString str;												//整数中作格式转换用
	int start = GetDlgItemInt(IDC_EDIT3);
	int end = GetDlgItemInt(IDC_EDIT5);							//交换一下，打印出来的就是正的
	int dis[M];													//单点到各点的最短路径数组
	int pre[M];													//存储前一个节点
	int visit[M];												//是否被访问

	//初始化
	memset(dis,INF, sizeof(dis));
	memset(pre, -1, sizeof(pre));
	memset(visit, 0, sizeof(visit));
	dis[start] = 0;
	visit[start] = 1;

	for (int j = 0; j < S.count; j++)									//把所有为0值变成无穷大
	{
		for(int i = 0; i < S.count; i++)
			if (S.mat.m[j][i] == 0)
			{
				S.mat.m[j][i] = INF;
			}
	}

	for (int i = 0; i < S.count; i++)									//将第一个点变为访问点
	{
			dis[i] = S.mat.m[start][i] + dis[start];
			pre[i] = start;
	}
	
	
	for (int j = 0; j < S.count; j++)
	{
		int min = INF;
		int mini = start;
		for (int i = 0; i < S.count; i++)
		{
			if (visit[i] == 0 && dis[i] < min)					//寻找相邻最小点
			{
				min = dis[i];
				mini = i;
			}
		}
		visit[mini] = 1;

		for (int i = 0; i < S.count; i++)						//更新其余未访问的边权
		{
			if (dis[i] > S.mat.m[mini][i] + dis[mini] && visit[i] == 0)
			{
				dis[i] = S.mat.m[mini][i] + dis[mini];
				pre[i] = mini;
			}
				
		}
		if (visit[end])											//找到终点并打印
		{
			int i = end;
			while (i != start)
			{
				Information += S.Pname[i] + Z;
				i = pre[i];
			}
			Information += S.Pname[i] + Y + Y;
			str.Format("%d", dis[end]);
			Information += X + str;
			SetDlgItemText(SCREEN, Information);
			MessageBox("最短距离已被加载");
			Information.Empty();
			break;
		}
		
	}

	// TODO: 在此添加控件通知处理程序代码
}

结果展示: