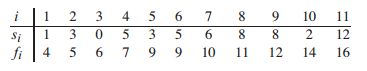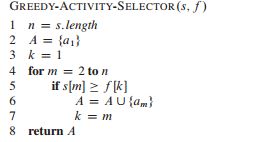算法导论 第十六章：贪心算法之单任务调度问题

  贪心算法是使所做的选择看起来都是当前最优的，通过所做的局部最优选择来产生一个全局最优解。

其具有的性质如下：

1）贪心选择性质：一个全局最优解可以通过局部最优（贪心）选择来达到。即，在考虑如何做选择时，我们只考虑对当前问题最佳的选择而不考虑子问题的结果。

          这一点是贪心算法不同于动态规划之处：在动态规划中，每一步都要做出选择，但是这些选择依赖于子问题的解。因此，解动态规划问题一般是自底向上，从小问题处理至大问题。在贪心算法中，我们所做的总是当前看似最优的选择，然后再解决选择之后所出现的子问题。贪心算法所做的当前选择可能依赖于已经做出的所有选择，但是不依赖于有待做出的选择或子问题的解，因此，贪心算法通常采用自顶向下的方式，一个一个地做出贪心选择，不断将给定的问题实例归约为更小的问题。

2）最优子结构：如果一个问题的一个最优解包含其子结构的最优解，则称该问题具有最优子结构。

   贪心算法和动态规划都利用了最优子结构性质，通常在用贪心算法求解问题时，能够给出一个动态规划解；但是能用动态规划解的的问题不一定能够用贪心算法求解。

贪心算法设计步骤：

1）  觉得问题的最优子结构

2）  设计一个递归解

3）  证明在递归解的任一阶段，最优选择之一总是贪心选择。

4）  证明通过贪心选择，所有子问题（除一个以外）都为空

5）  设计出一个实现贪心策略的递归算法

6）  将递归算法转换成迭代算法

 

活动选择问题

        假设有一个集合S={a(1),a(2),...,a(n)}, 每个活动i有一个开始时间s(i)和一个截止时间f(i),满足 0 ≤ s(i)< f(i) < ∞，若 s(i) ≥ f(j) 或 s(j) ≥ f(i)，则活动a(i) 和a(j)兼容。

活动选择问题就是选出一个由互相兼容的问题组成的一个最大子集合。

EG:

一个活动集合如下：

其最大子集有：{a(2),a(4),a(9),a(11)},{a(1),a(4),a(8),a(11)}等

分析：

1）最优子结构

定义集合S(i,j)表示每个活动在活动a(i)结束之后开始，活动a(j)开始之前结束的集合：

      

另外定义子问题的最大活动集为A(i,j)，则有：

        

设c[i,j]为S(i,j)中最大兼容子集中的活动数。则有：

2）贪心选择：

设任意的非空子集S(k),令a(m)是集合S(k)中具有最早结束时间的一个活动，则a(m)包含在最大兼容活动子集中。

求解：

1）递归贪心算法

伪代码如下：

当初始时活动的结束时间有序，则该算法运行时间为：Θ(n)

2)迭代贪心算法

伪代码如下：

当初始时活动的结束时间有序，则该算法运行时间为：Θ(n)

迭代贪心算法实现的活动选择问题完整代码如下：

#include
#include
#include
#include
using namespace std;


typedef struct Activity{
	int s;
	int f;
	}Activity;

bool a_less_b(const Activity &a,const Activity &b)
{
	return a.f > GA_ActivitySelect(Activity *a,int n)
{
	vector< vector > A;    //store the solutions
	vector act;

	for(int i=0;i temp;
		int k=i;
		temp.push_back(k+1);                 //subscript starts 0 
		for(int m=k+1; m= act[k].f){
				temp.push_back(m+1);
				k=m;
				}	
		A.push_back(temp);
		if(temp.size()!=A[0].size())
			A.erase(A.end()-1);
		}
	return A;

	}
void Print_Optimal(vector< vector > r)
{
	
	for(int i=0;i temp;
		temp=r[i];
		cout<<"The solution "< > res;          //maybe have many solutions
	res=GA_ActivitySelect(a,n);
	cout<<"The laregest activity set is:"<

运行结果：

该程序找出可能的解，但并没有找出所有满足要求的解。

【注：若有错误，请指正~~~】