Logistic Regression - Multi-class classification: One-vs-all
摘要: 本文是吴恩达 (Andrew Ng)老师《机器学习》课程,第七章《logistic回归》中第52课时《多分类》的视频原文字幕。为本人在视频学习过程中记录下来并加以修正,使其更加简洁,方便阅读,以便日后查阅使用。现分享给大家。如有错误,欢迎大家批评指正,在此表示诚挚地感谢!同时希望对大家的学习能有所帮助。
In this video, we’ll talk about how to get logistic regression to work for multi-class classification problems, and in particular, I want to tell you about an algorithm called one-versus-all classification.
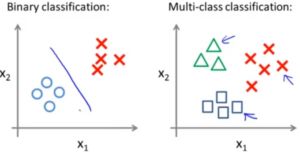
What’s a multi-class classification problem? Here are some examples. Let’s say you want a learning algorithm to automatically put your email into different folders, or to automatically tag your emails. So, you might have different folders or different tags for work email, email from your friends, email from your family, and emails about your hobby. And so, here we have a classification problem with 4 classes, which we might assign the numbers, the classes y=1, y=2, y=3 and y=4 too. And another example for a medical diagnosis: if a patient comes into your office with maybe a stuffy nose, the possible diagnoses could be that they’re not ill, maybe that’s y=1; or they have a cold, 2; or they have the flu, 3. And the 3rd and final example, if you are using machine learning to classify the weather, you know, maybe you want to decide the weather is sunny, cloudy, rainy or snow, or if there’s gonna be snow. And so, in all of these examples, y can take on a small number of discrete values, maybe 1 to 3, 1 to 4 and so on. And these are multi-class classification problems. And by the way, it doesn’t really matter whether we index as 0123 or 1234, I tend to index my classes starting from 1 rather than from 0, but either way, whatever, it really doesn’t matter.
Whereas previously, for a binary classification problem, our data sets look like this. For a multi-class classification problem, our data sets may look like this, where here, I’m using three different symbols to represent our three classes. So, the question is: given the data set with three classes, where this is an example of one class, that’s an example of the different class, and, that’s the example of yet, the third class. How do we get a learning algorithm to work for the setting? We already know how to do binary classification, using logistic regression, we know how the straight line, to separate the positive and negative classes. Using an idea of one-versus-all classification, we can then take this, and make it work for multi-class classification, as well.
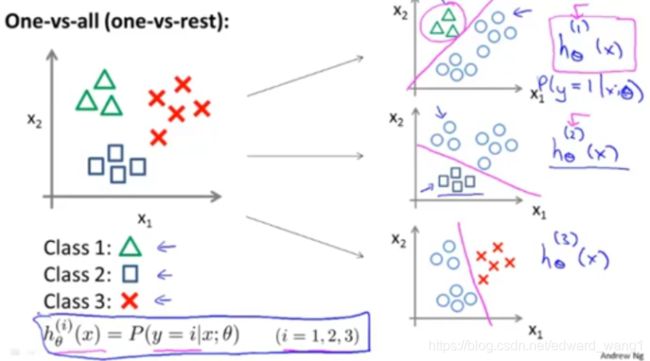
Here’s how one-versus-all classification works. And, this is also sometimes called “one-versus-rest.” Let’s say, we have a training set, like that shown on the left, where we have 3 classes. So, if y=1, we denote that with a triangle, if y=2, the square, and if y=3, then the cross. What we’re going to do is take a training set, and turn this into three separate binary classification problems. So I’ll turn this into three separate two-class classification problems. So let’s start with class 1, which is a triangle. We’re going to essentially create a new, sort of fake training set, where classes 2 and 3 get assigned to the negative class, and class 1 gets assigned to the positive class. We create a new training set, like that showing on the right, and we’re going to fit a classifier, which I’m going to call ![]() , where here, the triangles are the positive examples, and the circles are the negative examples. So, think of the triangles being assigned the value of 1, and circles, the value of 0s. And we’re just going to train a standard logistic regression classifier, and maybe that will give us a decision boundary that looks like that, ok? The superscript (1) here senses the class one. So, we’re doing this for the triangle of first class. Next, we do the same thing for class 2. Going to take the squares and assign the squares as the positive class, and assign everything else the triangles and the crosses as the negative class. And then we fit a second logistic regression classifier, I’m gonna call this
, where here, the triangles are the positive examples, and the circles are the negative examples. So, think of the triangles being assigned the value of 1, and circles, the value of 0s. And we’re just going to train a standard logistic regression classifier, and maybe that will give us a decision boundary that looks like that, ok? The superscript (1) here senses the class one. So, we’re doing this for the triangle of first class. Next, we do the same thing for class 2. Going to take the squares and assign the squares as the positive class, and assign everything else the triangles and the crosses as the negative class. And then we fit a second logistic regression classifier, I’m gonna call this ![]() , where the superscript (2) denotes that we’re now doing this: treating the square class as the positive class, and maybe we get the classifier like that. And finally, we do the same thing for the third class, and fit a third classifier
, where the superscript (2) denotes that we’re now doing this: treating the square class as the positive class, and maybe we get the classifier like that. And finally, we do the same thing for the third class, and fit a third classifier ![]() , and maybe this will give us a decision boundary or give us a classifier that separates the positive and negative examples like that. So, to summarize, what we’ve done is we fit 3 classifiers. So, for i equals 1 2 3, we’ll fit a classifier
, and maybe this will give us a decision boundary or give us a classifier that separates the positive and negative examples like that. So, to summarize, what we’ve done is we fit 3 classifiers. So, for i equals 1 2 3, we’ll fit a classifier ![]() , thus trying to estimate what is the probability that y is equal to class i given x and parameterized by
, thus trying to estimate what is the probability that y is equal to class i given x and parameterized by ![]() , right? So, in the first instance, for this first one up here, this classifier were learning to recognize the triangle, so it’s thinking of the triangles as a positive class. So,
, right? So, in the first instance, for this first one up here, this classifier were learning to recognize the triangle, so it’s thinking of the triangles as a positive class. So, ![]() is trying to estimate what is the probability that y=1, given x and parameterized by
is trying to estimate what is the probability that y=1, given x and parameterized by ![]() . And similarly, this is treating, you know, the square class as a positive class, so it’s trying to estimate the probability that y=2, and so on. So we now have 3 classifiers, each of which was trained is one of the three classes.
. And similarly, this is treating, you know, the square class as a positive class, so it’s trying to estimate the probability that y=2, and so on. So we now have 3 classifiers, each of which was trained is one of the three classes.
Just to summarize, what we’ve done is we’ve, we want to train a logistic regression classifier, ![]() for each class i to predict its probability y=i. Finally, to make a prediction, when we give a new input x, and we want to make a prediction, what we do is we just run our 3 of classifier on the input x, and then pick up the class (i) that maximums the three. So, we just basically pick the classifier, pick whichever one of the three classifier which is most confident, or most enthusiastically says that it thinks it has a right class. So, whichever value of (i), gives us the highest probability, we then predict y to be that value.
for each class i to predict its probability y=i. Finally, to make a prediction, when we give a new input x, and we want to make a prediction, what we do is we just run our 3 of classifier on the input x, and then pick up the class (i) that maximums the three. So, we just basically pick the classifier, pick whichever one of the three classifier which is most confident, or most enthusiastically says that it thinks it has a right class. So, whichever value of (i), gives us the highest probability, we then predict y to be that value.
So, that’s it for multi-class classification and one-versus-all method. And with this little method, you can now take the logistic regression classifier and make it work on multi-class classification problems as well.