五：逻辑回归

背景知识

最大似然估计

先记着怕明天忘了，特地去看了考研视频。
所谓最大似然估计，估计的是：当参数 = ？时，观测值所出现的概率最大。
举个宇哥的例子，迎面走来一个人，你不知道他是国家一级运动员，还是二级运动员。所以是骡子是马拉出来溜溜：
如果这个人打枪，打了5次，成绩是10,9,9,10,10环，那我推测这人十有八九是一级运动员
如果成绩是3,4,5,3,2环，那我推测这个人应该是二级运动员。
对应上面的定义，翻译如下：
当参数是一级运动员的情况下，成绩是10,9,9,10,10环 出现的概率是很大的。
当参数是二级运动员的情况下，成绩是3,4,5,3,2环 出现的概率是很大的。

具体深究：https://blog.csdn.net/zengxiantao1994/article/details/72787849

梯度下降法

梯度就是对一个多元函数的未知数求偏导,得到的偏导函数构成的向量就叫梯度
举个例子就明白了。比如二次函数 y = x2。导数：2x。
在 x = -1 时 导数为-2，方向是负的，即往坐标左侧，是增加最快的
在 x = 1 时 导数为2，方向是正的，即往坐标右侧，是增加最快的

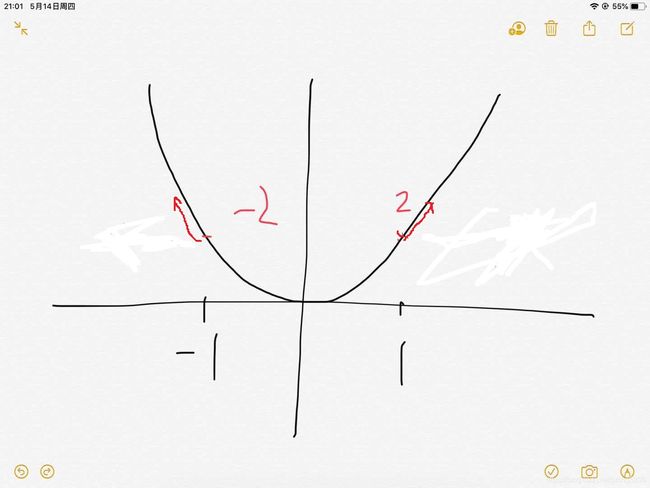
这个是一元,一元的梯度就是导数，
y = y - alpha*（该点梯度），alpha 是学习率，比如从（-1,1）点开始迭代，一次次变小，当到达（0,0）点时梯度为0，就不变了（理想情况，一般是会在0附近震荡，写程序时只要两次迭代后的y值差的绝对值小于某个阈值即可）
二元，多元都一样，往梯度方向是函数增加最快的方向，反梯度方向则是下降最快的方向。
详解：https://blog.csdn.net/UESTC_C2_403/article/details/74910107

逻辑回归

逻辑回归又叫对数回归。

引入

逻辑回归本质上也是一个二分类问题。

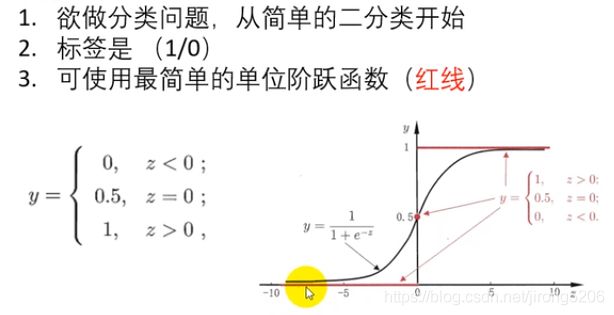
一般情况下红线（单位阶跃函数是一个最简单的二分类函数）
y=1,z>0；y=0, z<0,; 但是这个函数不是连续可导的，这给后续最优化问题会带来麻烦。所以就引入一个函数近似单位阶跃函数，但连续可导（图中黑线）。

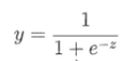
这个函数定义域是任意范围，值域在（0,1）之间，当z>0即y>0.5时，我们就可以归为15类，当z<0即y<0.5时归为0类。（注意，这个0.5是根据实际情况定的，有些情况，比如患癌概率是0.49，如果你按0.5的标准他是判定没有患癌症的，但从医学角度来看，还是极有可能患癌症，这边如果还用0.5会造成重大医疗事故，应该调小点，0.2，0.3这样，就是把上图y轴往左移一点）
那y知道了是关于类别label的，那z呢？z = XW。X是样本向量，W是权重向量。
示例：每个样本特征维度为二维时z的表达


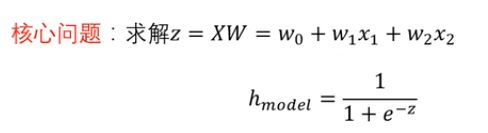
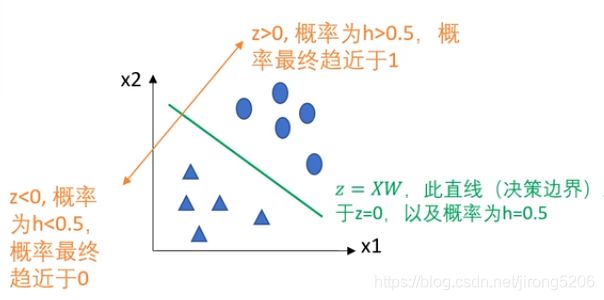
可以看到上图中的决策面，圆形在面上方z>0,属于1类，三角形在面下方z<0属于0类。

损失函数

理解方式1

我们目的是要找到一个好的决策面，那怎么找这个面呢？就像上文提到的SVM，关于求这个决策面都有损失函数指标，SVM中是margin越大越好，有物理意义。而逻辑回归的损失函数比较简单粗暴，就是预测错了，这个函数就会变大，且错的越离谱变的越大，所以只要将这个损失函数最小化，对应的决策面就会最优。

假设现在我有一个样本y,x。y是类别，x是特征向量。y的值是1也就是说这个样本是1类。然后我用x特征向量通过我的决策面函数预测我的分类：

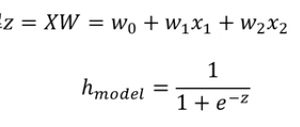
这样我就算出了h。
按照上面想的损失函数的作用的话：
以 h = 0.5为界限，
if h>0.5,分类正确，且随着h从0.5到1的不同，损失函数越来越小直至0。
if h<0.5,分类错误，且随着h从0.5到1的不同，损失函数越来越大直至无穷
引入下面的损失函数：

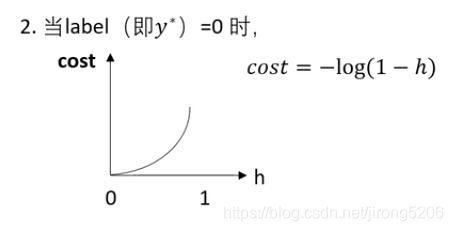
同理，假设现在我有一个样本y,x。y是类别，x是特征向量。y的值是0也就是说这个样本是0类。然后我用x特征向量通过我的决策面函数预测我的分类：
按照上面想的损失函数的作用的话：
以 h = 0.5为界限，
if h>0.5,分类错误，且随着h从0.5到1的不同，损失函数越来越大直至无穷。
if h<0.5,分类正确，且随着h从0.5到0的不同，损失函数越来越小直至0
引入下面的损失函数：

两者合并处理后最后的损失函数：

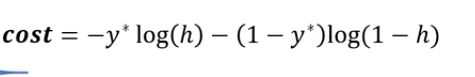
现在来梳理一下啊，cost -->h–>z–>xw 一步一步关联的
所以只要这个cost函数达到最小，所得出的W决定的决策面应该是最好的。

理解方式2

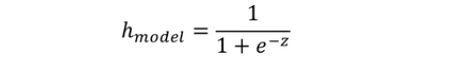
不难看出上述函数值域在（0,1）之间，可以把他理解为概率。
P(y=0|w,x) = 1 - h 预测为0的准确率
P(y=1|w,x) = h 预测为1的准确率
要使得这个决策面准确率越高 ，P就要越大。
引入 :P(正确率) =(h(w,x))^y * (1-h(w,x))^1-y
令Max( P )等价于 Max(log( p ))
推得：Max(y*log(h)+(1-y)log(1-h)) 等价于 理解方式一 ：Min(-ylog(h)-(1-y)*log(1-h))

最大似然估计

前文提到最大似然估计就是：当这个参数是什么时，这组特征才最有可能实现。翻译到这边就是：当W是什么的时候，P才会最大（P最大就意味着最有可能出现）
P = (h(w,x))^y * (1-h(w,x))^1-y 令这个最大，但这只是一个样本的。
若想让预测出的结果全部正确的概率最大,根据最大似然估计，就是所有样本预测正确的概率相乘得到的P(总体正确)最大，i 样本数共m个：

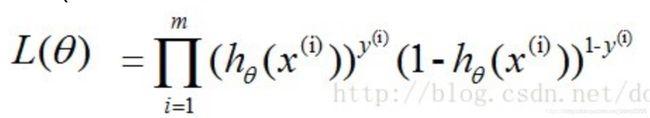
令上式最大。
取对数似然函数
我们最终需要是所有样本的准确率最高（sita 就是w）

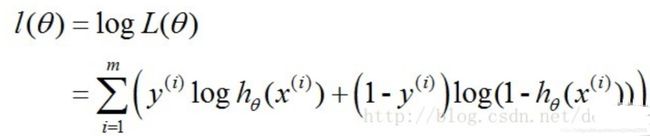
最优化问题中都是取最小，所以加个负号：

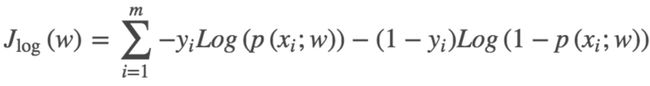
这个函数呢就是逻辑回归的损失函数 ------交叉熵损失函数

求解最优决策面

就是求是决策面最优的W

梯度下降法

参考：https://www.cnblogs.com/lliuye/p/9451903.html
例子：

随机梯度下降法

i表示样本数有1.2.3…m个
j表示每个样本维度数1.2.3…n维
alpha为学习率
这是对随机抽取的一个样本进行梯度计算

逻辑回归随机梯度下降推导：


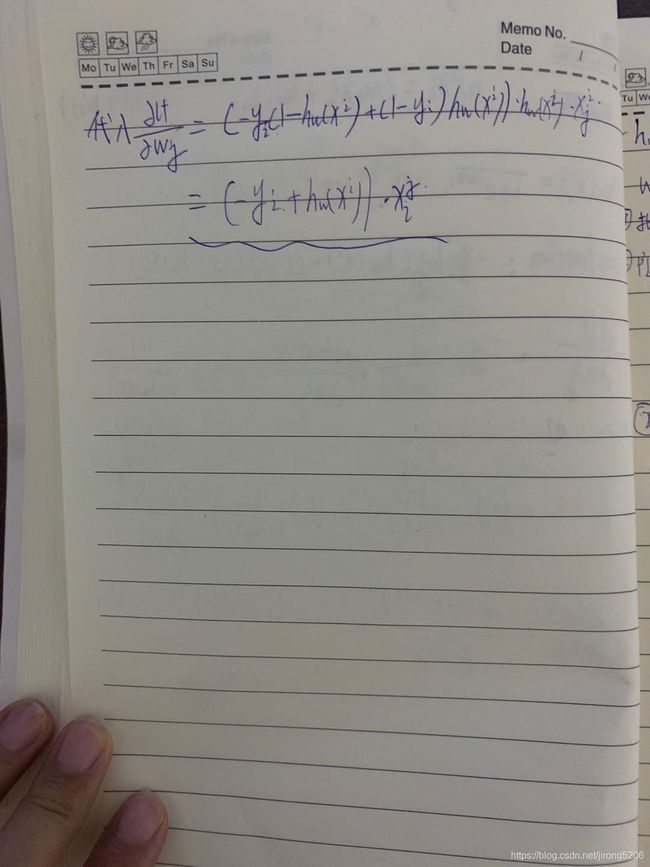
即可推出 。

批量梯度下降法

对所有样本进行梯度计算取平均

逻辑回归批量梯度下降推导：1/m是取平均

随机梯度下降法和批量梯度下降法优缺点

随机梯度下降法：
优点：在大样本中速度快，只需随机抽选一个样本进行计算。
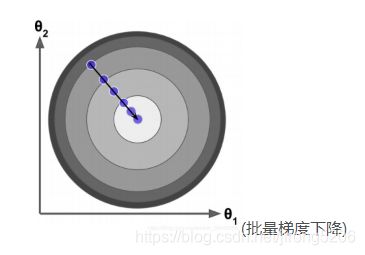
缺点：随机抽取的样本可能不能代表整体梯度下降方向，可能会出现这样
大样本中使用，小样本不推荐

批量梯度下降法：
优点：一般与总体梯度方向差不多。
缺点：大样本中计算量大，如果30w样本你要全算出来取平均：

小样本中使用大样本不推介。

用梯度下降法就能找到目标函数的最小值，确定W即可算出平面。

一对多分类

由于概率函数 hΘ(X) 所表示的是样本标记为某一类型的概率，但可以将一对一（二分类）扩展为一对多（one vs rest）：

将类型class1看作正样本，其他类型全部看作负样本，然后我们就可以得到样本标记类型为该类型的概率p1；

然后再将另外类型class2看作正样本，其他类型全部看作负样本，同理得到p2；

以此循环，我们可以得到该待预测样本的标记类型分别为类型class i时的概率pi，最后我们取pi中最大的那个概率对应的样本标记类型作为我们的待预测样本类型