Fisher's Linear Discriminant(LDA) 线性判别模型(2类)
Fisher’s Linear Discriminant(LDA) 线性判别模型
LDA(Linear Discriminant Analysis线,性判别分析),是一种supervised learning,是由Fisher在1936年提出的。 LDA通常作为数据预处理阶段的降维技术,其目标是将数据投影到低维空间来避免维度灾难(curse of dimensionality)引起的过拟合,同时还保留着良好的可分性。
一 LDA的引出
经常经过特征提取以后,我们需要进行降维。首先我们简化一下问题便于阐述其原理:假设在二维特征空间中,有**两类样本,**那么我们的目标就是对给定的数据集,将其投影到一条直线上,但是投影的方法有千千万万种,那么我们改选择什么样的投影呢?
首先我们的任务是为了分类服务的,那么我们需要投影后的样本尽可能的分开,最简单的度量类别之间分开程度的方式就是类别均值投影之后的距离。假设我们设置阈值 − w 0 -w_0 −w0,当 y ≥ − w 0 y \ge -w_0 y≥−w0 时,分类为 C 1 C_1 C1,否则分类到 C 2 C_2 C2 ,那我们将得到标准线性分类器。总的来说,将D维空间映射到一维空间会导致相当大的损失,在原始D维空间可以很好分类的特征映射到一维空间可能会出现相当大部分的重叠,如下图所示(左图为最大间隔度量的降维结果,这幅图中的两个类别在原始空维空间 ( x 1 ; x 2 ) (\boldsymbol x_1; \boldsymbol x_2) (x1;x2)中可以完美地被分开,但是当投影到连接它们的均值的直线上时,就有了一定程度的重叠)。但我们可以调整 w \boldsymbol w w来优化分类结果。
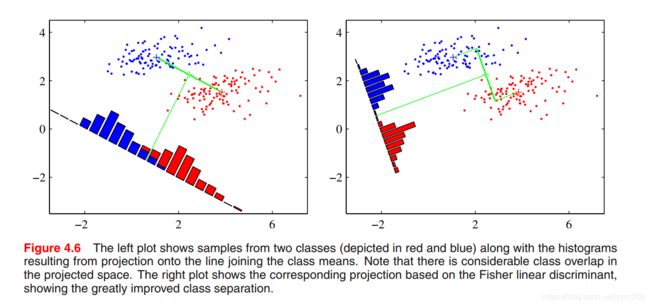
首先我们从简单的两分类问题说起,假设类 C 1 C_1 C1 有 N 1 N_1 N1个特征点,类 C 2 C_2 C2 有 N 2 N_2 N2个特征点,那么这两类数据的均值向量可以表示为:
μ i = 1 N i ∑ n ∈ C i x n , i = 1 , 2 \boldsymbol \mu_i = \frac{1}{N_i} \sum\limits_{n \in C_i} \boldsymbol x_n,\qquad i=1,2 μi=Ni1n∈Ci∑xn,i=1,2
一种比较好的投影方式就是利用不同类别的数据的中心来代表这类样本在空间中的位置,同时保证让投影之后的中心距离尽可能的大,也就是:
J ( w ) = μ ~ 2 − μ ~ 1 = w T ( μ 2 − μ 1 ) J(\boldsymbol w) = \tilde \mu_2 - \tilde \mu_1= \boldsymbol w^T(\boldsymbol \mu_2 - \boldsymbol \mu_1) J(w)=μ~2−μ~1=wT(μ2−μ1)
其中
μ ~ i = 1 N i ∑ y ∈ C i y = 1 N i ∑ x ∈ C i w T x = w T μ i \tilde \mu_i = \frac{1}{N_i}\sum\limits_{y \in C_i} \boldsymbol y = \frac{1}{N_i}\sum\limits_{x \in C_i} \boldsymbol w^T \boldsymbol x = \boldsymbol w^T \boldsymbol \mu_i μ~i=Ni1y∈Ci∑y=Ni1x∈Ci∑wTx=wTμi
μ ~ i \tilde \mu_i μ~i是类 C i C_i Ci的投影数据的均值, w T \boldsymbol w^T wT 是投影向量。但如果无限增大 w \boldsymbol w w ,这个表达式可以任意增大。为了解决这个问题,我们可以将 w \boldsymbol w w 限制为单位长度,即 ∥ w ∥ = ∑ i w i 2 = 1 \|\boldsymbol w \| =\sum\limits_i w_i^2 = 1 ∥w∥=i∑wi2=1 。若以上左图的投影方式,根据拉格朗日乘子法有 w ∝ ( μ 2 − μ 1 ) \boldsymbol w \propto (\boldsymbol {\mu_2 - \mu_1}) w∝(μ2−μ1), 但这样有一个问题就是,这两类样本在原始的二维空间 ( x 1 , x 2 ) (\boldsymbol {x_1,x_2}) (x1,x2) 可以很好地进行分类,但是投影以后却出现了重叠的情况。
因此,Fisher提出的思想:最大化一个函数,这个函数能够让类均值的投影分开得较大,同时让每个类别内部的方差较小,从而最小化了类别的重叠。
这也是LDA的中心思想即:最大化类间距离,最小化类内距离。
二 LDA算法推导(2类)
接着上一段的引出,我们已经找到了一种不错的投影方式,现在只需要让其最小化类内的方差,我们假设投影结束后,样本的坐标为 $ y_n$ ,即 y n = w T x n \boldsymbol y_n = \boldsymbol w^T \boldsymbol x_n yn=wTxn ,那么来自类别 C k C_k Ck 的数据经过变换后的类内方差为:
s ~ k 2 = ∑ n ∈ C k ( y n − μ ~ k ) \tilde s_k^2 = \sum\limits_{n \in C_k} (y_n - \tilde \mu_k) s~k2=n∈Ck∑(yn−μ~k)
我们可以把整个数据集的总的类内方差定义为 $\tilde s_1^2 + \tilde s_2^2 $ 。Fisher准则根据类间距离和类内方差的比值定义,即:
a r g m a x J ( w ) = ( μ ~ 1 − μ ~ 2 ) 2 s ~ 1 2 + s ~ 2 2 arg \ max J(w) = \frac{(\tilde \mu_1 - \tilde \mu_2)^2}{\tilde s_1^2 + \tilde s_2^2 } arg maxJ(w)=s~12+s~22(μ~1−μ~2)2
根据 μ ~ k = w T μ k \tilde \mu_k = \boldsymbol w^T \boldsymbol \mu_k μ~k=wTμk ,以及 y = w T x y = \boldsymbol w^T \boldsymbol x y=wTx ,对上式子进行改写, μ ~ 1 − μ ~ 2 \tilde \mu_1 - \tilde \mu_2 μ~1−μ~2 通过:
( μ ~ 1 − μ ~ 2 ) 2 = ( w T μ 1 − w T μ 2 ) 2 = w T ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T w = w T S B w (\tilde \mu_1 - \tilde \mu_2 )^2= (\boldsymbol{ w^T \mu_1 - w^T \mu_2)^2 = w^T(\mu_1 - \mu_2)(\mu_1 - \mu_2)^Tw = w^TS_Bw} (μ~1−μ~2)2=(wTμ1−wTμ2)2=wT(μ1−μ2)(μ1−μ2)Tw=wTSBw
$\tilde s_1^2 + \tilde s_2^2 $通过下式:
s ~ i 2 = ∑ n ∈ C i ( y n − μ ~ i ) 2 = ∑ y ∈ C i ( w T x − w T μ i ) 2 = ∑ y ∈ C i w T ( x − μ i ) ( x − μ i ) T w \tilde s_i^2 = \sum\limits_{n \in C_i}(y_n-\tilde \mu_i)^2 = \boldsymbol{\sum\limits_{y \in C_i}(w^Tx-w^T\mu_i)^2 = \sum\limits_{y \in C_i}w^T(x-\mu_i)(x-\mu_i)^Tw} s~i2=n∈Ci∑(yn−μ~i)2=y∈Ci∑(wTx−wTμi)2=y∈Ci∑wT(x−μi)(x−μi)Tw
J ( w ) J(w) J(w)可以被重写为:
J ( w ) = w T S B w w T S w w \boldsymbol{J(w) = \frac{w^TS_Bw}{w^TS_ww}} J(w)=wTSwwwTSBw
其中 S w \boldsymbol S_w Sw是类间(between-class)散度矩阵,形式为
S B = ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T \boldsymbol{S_B = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T} SB=(μ1−μ2)(μ1−μ2)T
S w \boldsymbol S_w Sw被称为类内(within-class)散度矩阵,形式为:
S w = ∑ x ∈ c 1 ( x − μ 1 ) ( x − μ 1 ) T + ∑ x ∈ c 2 ( x − μ 2 ) ( x − μ 2 ) T \boldsymbol{S_w = \sum\limits_{x \in c_1}(x-\mu_1)(x-\mu_1)^T + \sum\limits_{x \in c_2}(x-\mu_2)(x-\mu_2)^T} Sw=x∈c1∑(x−μ1)(x−μ1)T+x∈c2∑(x−μ2)(x−μ2)T
对公式 J ( w ) J(\boldsymbol{w}) J(w)关于 w \boldsymbol{w} w 求导,并另之为 0,我们发现 J ( w ) J(\boldsymbol{w}) J(w) 取得最大值的条件为:
∂ J ( w ) ∂ w = 2 S B w ⋅ w T S w w − w T S B w ⋅ 2 S B w w T S w w = 0 ⇒ ( w T S B w ) S w w = ( w T S w W ) S B w \frac{\partial{J(\boldsymbol w)}}{\partial{\boldsymbol w}} = \frac{\boldsymbol{2S_Bw \cdot w^TS_ww - w^TS_Bw \cdot 2S_Bw}}{\boldsymbol {w^TS_ww}}= 0 \\ \Rightarrow \boldsymbol{(w^TS_Bw)S_ww = (w^TS_wW)S_Bw} ∂w∂J(w)=wTSww2SBw⋅wTSww−wTSBw⋅2SBw=0⇒(wTSBw)Sww=(wTSwW)SBw
由于 w T S B w \boldsymbol{w^TS_Bw} wTSBw 和 w T S w w \boldsymbol{w^TS_ww} wTSww 在简化的二分类问题中都是标量,因此我们可以把上式子看做:
S B w = λ S w w \boldsymbol{S_Bw} = \lambda \boldsymbol{S_ww} SBw=λSww
(或者将分母限定在模为1,利用拉格朗日求解也可以得到上式,具体参考周志华《机器学习》)。将求导后的结果两边都乘以 S w − 1 S_w^{-1} Sw−1 可得:
S w − 1 S B w = λ w \boldsymbol{S_w^{-1}S_Bw} = \lambda \boldsymbol{w} Sw−1SBw=λw
从这里就可以看出,是一个求特征值和特征向量的问题了。具体地,对于我们在引出中提出的简化问题,由于:
μ ~ 2 − μ ~ 1 = w T ( μ 2 − μ 1 ) ⇒ ( μ ~ 2 − μ ~ 1 ) T = ( μ 2 − μ 1 ) T w ⇒ ( μ 2 − μ 1 ) ( μ ~ 2 − μ ~ 1 ) T = ( μ 2 − μ 1 ) ( μ 2 − μ 1 ) T w = S B w \tilde \mu_2 - \tilde \mu_1= \boldsymbol w^T(\boldsymbol \mu_2 - \boldsymbol \mu_1) \\ \Rightarrow (\tilde \mu_2 - \tilde \mu_1)^T= (\boldsymbol \mu_2 - \boldsymbol \mu_1)^T \boldsymbol w \\ \Rightarrow (\boldsymbol \mu_2 - \boldsymbol \mu_1)(\tilde \mu_2 - \tilde \mu_1)^T= (\boldsymbol \mu_2 - \boldsymbol \mu_1)(\boldsymbol \mu_2 - \boldsymbol \mu_1)^T\boldsymbol w = \boldsymbol { S_Bw}\\ μ~2−μ~1=wT(μ2−μ1)⇒(μ~2−μ~1)T=(μ2−μ1)Tw⇒(μ2−μ1)(μ~2−μ~1)T=(μ2−μ1)(μ2−μ1)Tw=SBw
因此 S B w \boldsymbol{S_Bw} SBw的方向始终为 μ 2 − μ 1 \boldsymbol{\mu_2 - \mu_1} μ2−μ1 ,故可以用 λ ( μ 2 − μ 1 ) \lambda(\boldsymbol{\mu_2 - \mu_1}) λ(μ2−μ1) 来表示,因此我们可以得到:
w ∝ S w − 1 ( μ 2 − μ 1 ) \boldsymbol{w \propto S_w^{-1}(\mu_2 - \mu_1)} w∝Sw−1(μ2−μ1)
由于对 w \boldsymbol w w 扩大缩小任何倍不影响结果,因此我们可得:
w = S w − 1 ( μ 2 − μ 1 ) \boldsymbol{w = S_w^{-1}(\mu_2 - \mu_1)} w=Sw−1(μ2−μ1)
我们只需要求出原始样本的均值和方差就可以求出最佳的方向 w \boldsymbol w w,这就是Fisher于1936年提出的线性判别分析。
