【网络流】最大流:最大流判定,拆点,建图实战
最大流判定
秘密挤奶机
原题链接
给出一张包含 N N N个点, P P P条边的无向图, 1 → N 1\rightarrow N 1→N走 T T T次,每条边最多走 1 1 1次。
问: T T T条路径中最大边权的最小值。
用 d i n i c + dinic+ dinic+二分。
判定问题:在无向图中,删除大于 m i d mid mid的边,查找边权 ≤ m i d \leq mid ≤mid的边, 1 → N 1\rightarrow N 1→N是否存在 T T T条没有公共边的路径。
S = 1 , T = n S=1,T=n S=1,T=n,最大可行流流量 = = =路径数。 ≥ T \geq T ≥T时合法。
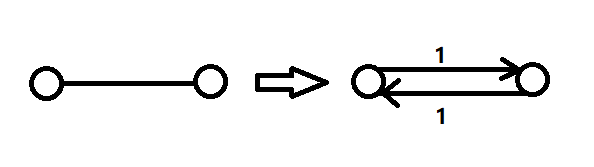
①若同一条边正反向都流过 1 1 1的流量:相当于没走过这条边。
删去这两条边的流量:满足容量限制。满足流量守恒:少流进的流量等于少流出的流量。
②边可以合并。
③可行流与不相交的路径一一对应。
代码如下:
#include
using namespace std;
const int N=200+10;
const int M=100000+10;
const int INF=1e9;
int n,m,K,S,T;
int h[N],ve[M],c[M],w[M],ne[M],id;
int q[N],d[N],cur[N];
void add(int x,int y,int z){
ve[id]=y;w[id]=z;ne[id]=h[x];h[x]=id++;
ve[id]=x;w[id]=z;ne[id]=h[y];h[y]=id++;
}
bool bfs(){
int he=0,ta=0;
memset(d,-1,sizeof d);
q[0]=S;d[S]=0;cur[S]=h[S];
while(he<=ta){
int x=q[he++];
for(int i=h[x];~i;i=ne[i]){
int y=ve[i];
if(d[y]==-1&&c[i]){
d[y]=d[x]+1;
cur[y]=h[y];
if(y==T)return true;
q[++ta]=y;
}
}
}
return false;
}
int dfs(int u,int limit){
if(u==T)return limit;
int flow=0;
for(int i=cur[u];~i&&flowmid)c[i]=0;
else c[i]=1;
return dinic()>=K;
}
int main(){
scanf("%d%d%d",&n,&m,&K);
S=1;T=n;
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
}
int l=1,r=1e6;
while(l>1;
if(check(mid))r=mid;
else l=mid+1;
}
printf("%d",r);
return 0;
}
星际转移问题
原题链接
①用并查集判断 0 0 0与 n + 1 n+1 n+1是否联通。
②若有解:用 d a y day day天,能否将所有人运到月球。
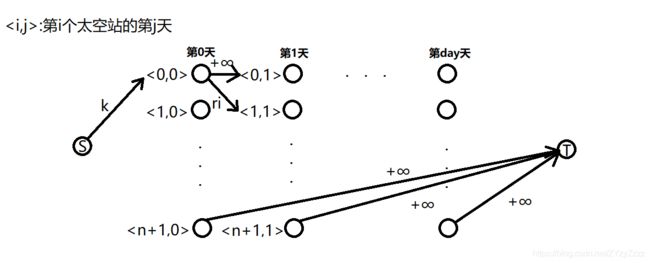
需要用到分层图的思想。
①从 S S S向 < 0 , 0 > <0,0> <0,0>连一条容量为 k k k的边。
从 < i , d a y >
②对于太空船:在邻天的太空站之间连一条容量为 r i r_i ri$的边。
③等待:对于相邻天的同一太空站,连一条容量为 + ∞ +∞ +∞的边。
d a y day day从小到大枚举(比二分好):结构与 d a y day day成正比, d a y day day增大,网络增大。
代码如下:
#include
using namespace std;
const int N=30000+10;
const int M=40000+10;
const int INF=1e9;
int n,m,k,S,T;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N];
struct Ship{
int h,r,v[30];
}sh[30];
int fa[30];
int find(int x){
if(fa[x]==x)return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
fa[find(x)]=find(y);
}
int get(int i,int day){
return day*(n+2)+i;
}
void add(int x,int y,int z){
ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}
bool bfs(){
int he=0,ta=0;
memset(d,-1,sizeof d);
q[0]=S;d[S]=0;cur[S]=h[S];
while(he<=ta){
int x=q[he++];
for(int i=h[x];~i;i=ne[i]){
int y=ve[i];
if(d[y]==-1&&c[i]){
d[y]=d[x]+1;
cur[y]=h[y];
if(y==T)return true;
q[++ta]=y;
}
}
}
return false;
}
int dfs(int u,int limit){
if(u==T)return limit;
int flow=0;
for(int i=cur[u];~i&&flow=k)break;
day++;
}
printf("%d",day);
}
return 0;
}
拆点
餐饮
原题链接
给每头奶牛一份食物,一份饮料,每种食物或饮料都只有一份,求最多满足几头奶牛。
类似于二分图匹配的建图方式:

但可行流不一定对应原题的解。可能会有很多组食物和饮料共用一头牛。
因此需要用到拆点的思想。
将每头牛拆成两个点,即入点与出点,在入点与出点之间连一条容量为 1 1 1的边,即可保证一头牛只匹配一份食品和一个饮料。
代码如下:
#include
using namespace std;
const int N=500+10;
const int M=50000+10;
const int INF=1e9;
int n,f,d,S,T;
int h[N],ve[M],c[M],ne[M],id;
int dep[N],q[N],cur[N];
void add(int x,int y,int z){
ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}
bool bfs(){
int he=0,ta=0;
memset(dep,-1,sizeof dep);
q[0]=S;dep[S]=0;cur[S]=h[S];
while(he<=ta){
int x=q[he++];
for(int i=h[x];~i;i=ne[i]){
int y=ve[i];
if(dep[y]==-1&&c[i]){
dep[y]=dep[x]+1;
cur[y]=h[y];
if(y==T)return true;
q[++ta]=y;
}
}
}
return false;
}
int dfs(int u,int limit){
if(u==T)return limit;
int flow=0;
for(int i=cur[u];~i&&flow 最长递增子序列问题
原题链接
①用 d p dp dp求出最长递增子序列的长度。
②当 f [ i ] f[i] f[i]可以由 f [ j ] + 1 f[j]+1 f[j]+1更新时( w [ j ] < = w [ i ] , j < i w[j]<=w[i],jw[j]<=w[i],j<i),从 j j j向 i i i连一条容量为 1 1 1的边。因为每个点只能用一次,因此进行拆点,每个入点与出点之间连一条容量为 1 1 1的边。若 f [ i ] = = 1 f[i]==1 f[i]==1,从 S S S向 i i i的入点连一条容量为 1 1 1的边;若 f [ i ] = = s f[i]==s f[i]==s,从 i i i的出点向 T T T连一条容量为 1 1 1的边。
③枚举每条边,若为从 S S S向 1 1 1号点的出点连的边、 1 1 1号点的入点与出点连的边、 n n n号点的入点与出点连的边、从 n n n号点的出点向 T T T连的边,都将容量改为 + ∞ +∞ +∞。(在第三问中, 1 1 1号点、 n n n号点都可以用无数次)重建好图后,在第二问中的残留网络再做一次 d i n i c dinic dinic即可,答案需要累加上第二问的答案。
注意:若 s = = 1 s==1 s==1,那么后面两个答案都为 n n n。
代码如下:
#include
using namespace std;
const int N=1000+10;
const int M=300000+10;
const int INF=1e9;
int n,S,T;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N];
int g[N],w[N];
void add(int x,int y,int z){
ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}
bool bfs(){
int he=0,ta=0;
memset(d,-1,sizeof d);
q[0]=S;d[S]=0;cur[S]=h[S];
while(he<=ta){
int x=q[he++];
for(int i=h[x];~i;i=ne[i]){
int y=ve[i];
if(d[y]==-1&&c[i]){
d[y]=d[x]+1;
cur[y]=h[y];
if(y==T)return true;
q[++ta]=y;
}
}
}
return false;
}
int dfs(int u,int limit){
if(u==T)return limit;
int flow=0;
for(int i=cur[u];~i&&flow 企鹅游行
原题链接
代码及解析如下:
#include
#define x first
#define y second
using namespace std;
typedef pairPII;
const int N=200+10;
const int M=30000+10;
const int INF=1e9;
const double eps=1e-8;
int n,S,T;
double D;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N];
PII p[N];
bool check(PII a,PII b){//企鹅能否从冰块a跳到冰块b或从冰块b跳到冰块a
double dx=a.x-b.x,dy=a.y-b.y;
return dx*dx+dy*dy 建图实战
猪
原题链接
此题要注意时序。建图时建三种边。
①若当前顾客是第一次打开猪舍的顾客,那么从 S S S向当前顾客连一条容量为猪舍内初始猪量的边。
②若当前顾客不是第一次打开猪舍的顾客,那么从上一个打开该猪舍的顾客向当前顾客连一条容量为 + ∞ +∞ +∞的边,表示之前顾客所能打开的猪舍中猪(除去之前顾客已买走的猪)当前顾客可以继承。
③从当前顾客向 T T T连一条容量为要购买猪的数量的边。
#include
using namespace std;
const int N=100+10;
const int M=30000+10;
const int K=1000+10;
const int INF=1e9;
int n,m,S,T;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N];
int w[K],last[K];//w[i]:猪舍i猪的数量;last:上一次打开猪舍i的顾客的编号
void add(int x,int y,int z){
ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}
bool bfs(){
int he=0,ta=0;
memset(d,-1,sizeof d);
q[0]=S;d[S]=0;cur[S]=h[S];
while(he<=ta){
int x=q[he++];
for(int i=h[x];~i;i=ne[i]){
int y=ve[i];
if(d[y]==-1&&c[i]){
d[y]=d[x]+1;
cur[y]=h[y];
if(y==T)return true;
q[++ta]=y;
}
}
}
return false;
}
int dfs(int u,int limit){
if(u==T)return limit;
int flow=0;
for(int i=cur[u];~i&&flow