当实证资产定价遇上机器学习

2020年的 Review of Financial Studies刊出了一篇名为“ Empirical Asset Pricing via Machine Learning”的文章，作者中有两位是在Booth的华人顾诗颢、修大成，另一位则是在耶鲁和 AQR任职的 Bryan Kelly。

该文对使用机器学习做实证资产定价的经典问题（即测度资产的风险溢价）进行了可比较的分析，表明使用机器学习的投资者可获得巨大的经济收益，甚至可比现有文献中基于回归的策略表现高出一倍。该文确定出最佳的模型（树和神经网络），并追踪到它们预测的增量收益来自于预测因子的交互，这恰恰是其他方法所错失的部分。所有的方法找出的最佳预测信号集是一致的，其中包含了动量、流动性、波动性的相关变量。

将机器学习应用于金融市场，在业界早已不是什么新鲜事，在量化投资领域中更是一个老生常谈的问题，它的有效性和可靠性也一直存在不少争论。而在金融学术界，之前只有寥寥数篇文章涉及到一部分机器学习中的方法，常态化地使用机器学习则是在最近才出现的苗头。从学术角度来说，该文是比较有代表性的一篇，基本上把机器学习能玩的东西全都玩了一遍。

1 为什么是机器学习？

首先，是实证资产定价领域本身的特点，让人将它和机器学习进行联想：

1. 现代实证资产定价研究有两个主题，一是描述和理解不同资产的期望收益率的差异，另一个是研究总体股权风险溢价的动态特性。而测度一项资产的风险溢价，本质上是一个预测问题——风险溢价就是未来实现的超额收益率的条件期望；
2. 对风险溢价来说，备选的变量集合非常大；
3. 高维预测因子进入风险溢价的函数形式是不确定的。

其次，机器学习本身的特点，又使得它适用于这种不确定函数形式的问题：

1. 多样性。它有各种不同的算法，可以搜索很大的函数空间；
2. 它的各种算法可以对复杂的非线性关系进行近似；
3. 它有参数惩罚和模型选择标准，哪怕函数形式非常广泛，也可以避免过拟合偏差和错误发现。

正是上述种种特性，让人觉得将实证资产定价与机器学习相结合是一件很自然的事情。

2 方法总览

为避免过多的公式堆积，本节仅仅对该文所用的方法做个概述。

一项资产的超额收益可表述成一个加性的预测误差模型（additive prediction error model）：

$$r_{i,t+1}=E_t(r_{i,t+1})+{ϵ}_{i,t+1}$$

其中

$$E_t(r_{i,t+1})=g^{\star }(z_{i,t})$$

也就是说，我们的目的是，分离出一个 $E_t(r_{i,t+1})$ 的表示形式，它是预测因子的函数，并对 $r_{i,t+1}$ 有最大的样本外解释力。其中预测因子是高维的 $z_{i,t}$，函数形式可以是灵活的条件期望收益率函数 $g^{\star }(\cdot )$，在这里假设函数形式与 $i$ 和 $t$ 均无关。

2.1 用验证（Validation）进行样本划分和调参

该文将数据集划分成 3 个不相邻的时间区间：

• 训练集，用于训练数据；
• 验证集，用于选择超参数；
• 测试集，用于评估模型的预测表现。

对于本文 60 年的数据集，在开始时，先将前 18 年作为训练集，中间 12 年作为验证集，后面 30 年作为测试集。当用训练集和验证集完成一次模型估计后，对后续那年的测试集数据作出预测，并评估表现。然后将训练集向后增加一年，把验证集窗口往后挪一年并依旧保持 12 年的长度，再次进行模型估计后，再对接下来的一年的测试集数据作出预测并评估。如此往复。

2.2 各种机器学习算法

第一个算法是线性模型，它与计量经济学中的线性回归非常类似，也同样可用最小化误差的平方和（在机器学习中也叫目标函数或损失函数）求解参数。

由于该文所用数据是面板数据，不同年份的股票数不一样，因此可在每个误差平方项的权重上做一些调整。比如可以将每个样本的误差平方项的权重设为该年股票数的倒数，这样就可以使每一年在损失函数中的权重相等。也可以将每个样本的误差平方项的权重设为正比于该股票在该年的市值，这样可使预测的准确性向大市值股票倾斜。

另外，由于误差的平方是一个二次函数，它的凸性使得当误差较大时它的平方和异常大，这会影响基于 OLS 的预测的稳定性。为解决这个问题，可使用Huber 稳健的目标函数，也即当误差大于一个阈值时，让它从平方形式变成一次形式。

当预测因子过多时，传统的线性模型会出现对噪声过拟合，而收益率预测问题的信噪比极低，这就导致它的表现会非常差。此时可通过加入惩罚项来避免过拟合。按线性模型中加入的惩罚项形式不同，可分为 LASSO、Ridge 等，该文使用的是 LASSO 和 Ridge 的结合，即弹性网络（elastic net）模型。

此外，该文还使用了两种降维模型：主成分回归（PCR）和偏最小二乘（PLS）：

• PCR 的思想是先用一系列低维的“成分”来表示高维的预测因子，在这过程中尽可能不损失原来的信息，找出的第一个“成分”就叫主成分（PC）。再用得到的一系列成分对目标变量做回归。PCR 仅仅是在预测因子一侧做变换，要求尽可能多地保留预测因子的信息，没有考虑要预测的目标变量，因此也没有考虑找出的“成分”的预测能力。
• PLS 则考虑了预测因子的预测能力，它先用每个预测因子对目标变量做单变量预测回归，再以得到的系数为权重，将所有的预测变量做加权平均，得到第一个成分，再接着，把预测因子和目标变量都对之前得到的成分做正交化，再不断重复之前的过程，最终也得到一系列成分。

以上的模型都是参数模型，下面是一些非参模型。

广义线性模型（Generalized linear model），就是用样条函数对预测因子作展开。该文使用最小平方形式的目标函数，对加和不加 Huber 稳健修正都进行了尝试，对于惩罚函数则选择了“Group LASSO”的形式。

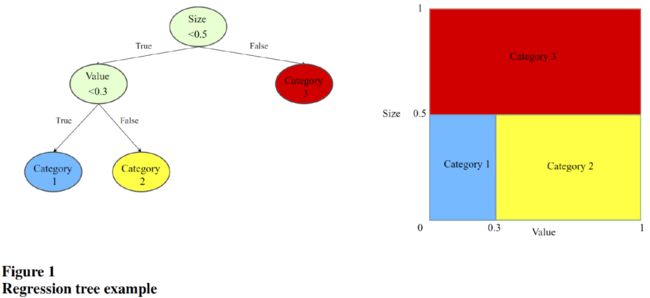
该文还使用了提升的（Boosted）回归树和随机森林模型。它们的基础都是树模型，树模型的思想就是根据数据不断地进行分支，在做出新的分支时尽可能地提高每个分支的“纯度”。

树模型的灵活度非常高，很容易发生过拟合，在树模型的基础上，可以用“集成（ensemble）”方法提高稳健性，有两种常用的“集成”方法：

• Boosting 法。将很多“极其简单”的树加总在一起，该文用的是比较流行的梯度提升回归树（GBRT）；
• Bagging 法。对数据集不断进行 Boostrap 抽样，针对每次抽样出的数据子集训练一棵树，最后将所有的树综合在一起，这就是随机森林（random forest）。

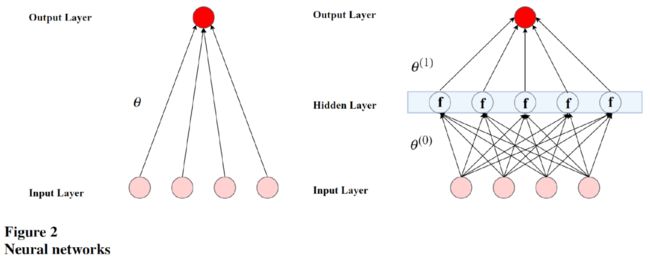
最后是神经网络模型。它的基本结构如图所示：

该文使用了含 1-5 层隐含层的全连接网络结构，其中 NN1 的隐含层有 32 个节点，NN2 分别有 32、16 个节点，以此类推，NN5 有 32、16、8、4、2 个节点。

由于神经网络的高度非线性和非凸性，需使用随机梯度下降算法（SGD）进行训练。此外，该文加入了 l1 正则项的同时，还用了 4 种其他手段进行正则化：learning rate shrinkage，early stopping，batch normalization，以及 ensembles。

2.3 模型表现评价

该文通过计算样本外$R^2$ 评价模型：

$$R_{OOS}^2=1-\frac{{\sum }_{(i,t)\in {\mathcal{T}}_3}(r_{i,t+1}-{\hat{r}}_{i,t+1}{)}^2}{{\sum }_{(i,t)\in {\mathcal{T}}_3}{r}_{i,t+1}^2}$$

和计量经济学中传统的 $R^2$ 的不同之处有两点，一是计算时只考虑测试集 ${\mathcal{T}}_3$ 中的点，二是分母没有做去均值（demeaning）的操作。第二点是因为对于预测未来股票的超额收益率来说，与其用历史均值去猜测它未来的收益率，还不如直接用 0 来猜，历史均值的噪声太大了，导致如果用它作为基准，标准太松。因此该文在分母中不做 demeaning，这相当于用 0 代替了均值，这样分母更小，$R_{OOS}^2$ 也更低，标准变得更加严格了。

另外，该文对 Diebold-Mariano（1995）检验做了改进，得出修正的DM 检验统计量。

2.4 变量的重要性和边际关系

该文用两种方式评价变量的重要性：

• 当保持其余所有变量不变，将某个变量的所有的值都设为 0 时，看整个预测 $R^2$ 的下降程度；
• 计算对某个输入变量的偏导数平方和（sum of squared partial derivatives，SSD），详见 Dimopoulos，Bourret 和 Lek（1995）。

另外，该文还追踪了每个变量和期望收益率的边际关系，对于一阶的关系，可以可视化地呈现出来。

3 实证效果

3.1 数据

从 CRSP 数据库中拿出在 NYSE、AMEX 和 NASDAQ 上市的股票，从 1957 年 3 月到 2016 年 12 月的数据。拿出 94 个公司层面特征，74 个行业虚拟变量，8 个宏观预测因子，将 94 个公司层面特征和 8 个宏观预测因子分别做交互项，最终有 $94\times (1+8)+74=920$ 个变量。

3.2 模型比较

下图展示了各模型的月度 $R_{OOS}^2$，并分别在全样本市值最大/最小的 1000 个股票中进行检验：

对于整个训练过程，一些模型的复杂度变化如下图：

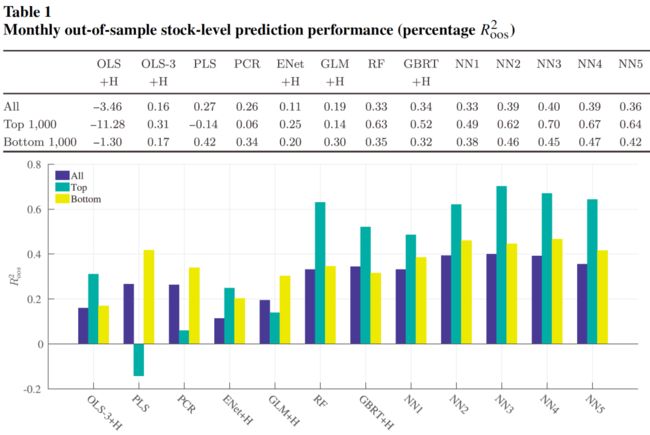
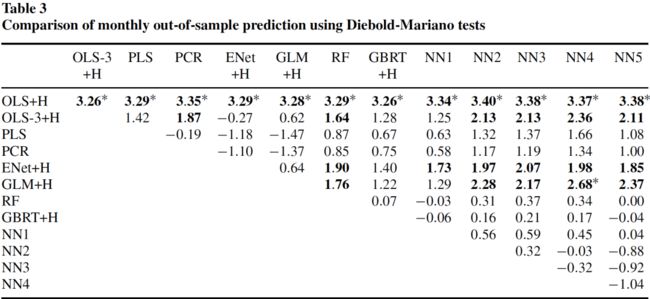
以年为时间跨度，再次比较各模型的 $R_{OOS}^2$：

Diebold-Mariano 检验统计量：

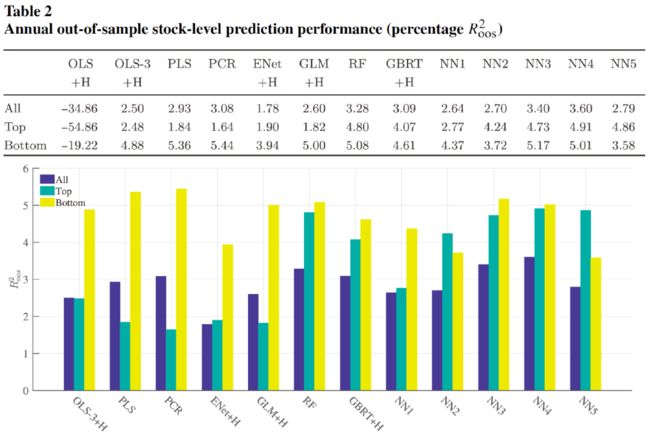
其中正的数值表示列的模型优于行的模型，黑体表示在 5%的显著性水平上显著。同时，该表还展示了Bonferroni multiple comparison的结果，星号表示在 5%显著性水平上显著。

3.3 哪些变量重要？

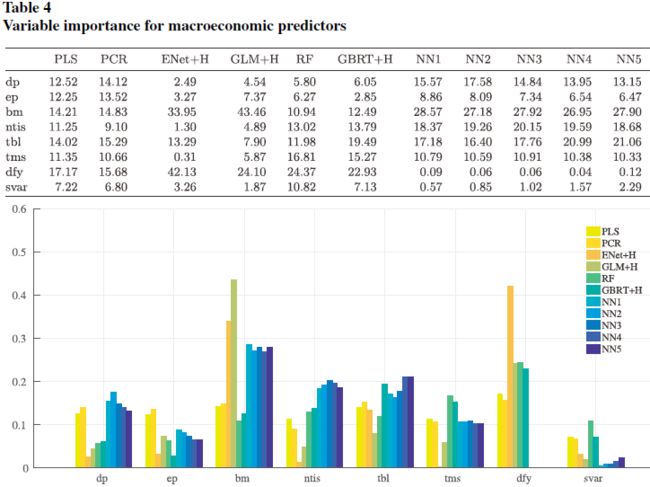
分别将每个变量在所有出现的地方都设为 0，计算 $R^2$ 的减少。变量的重要性情况如下：

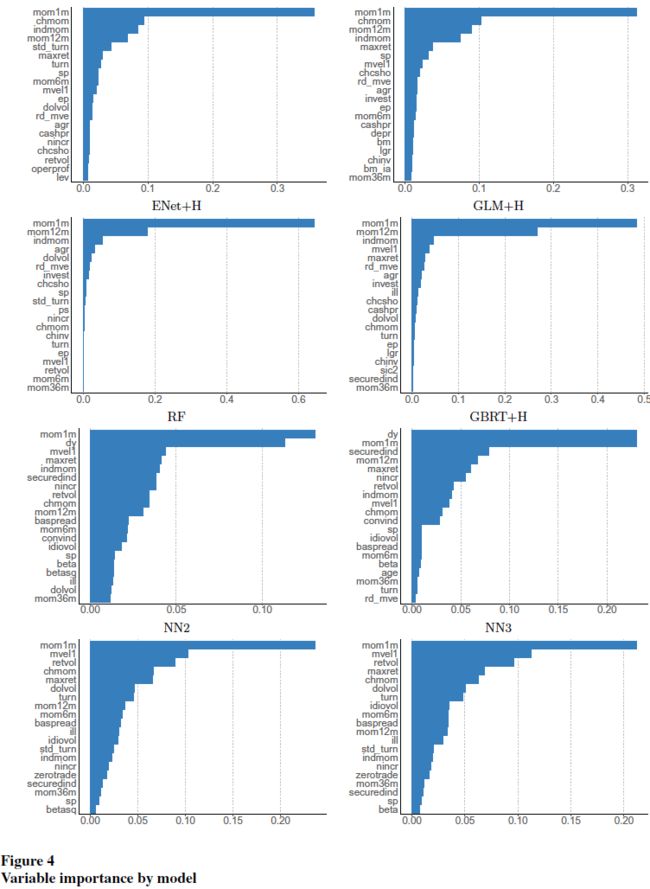
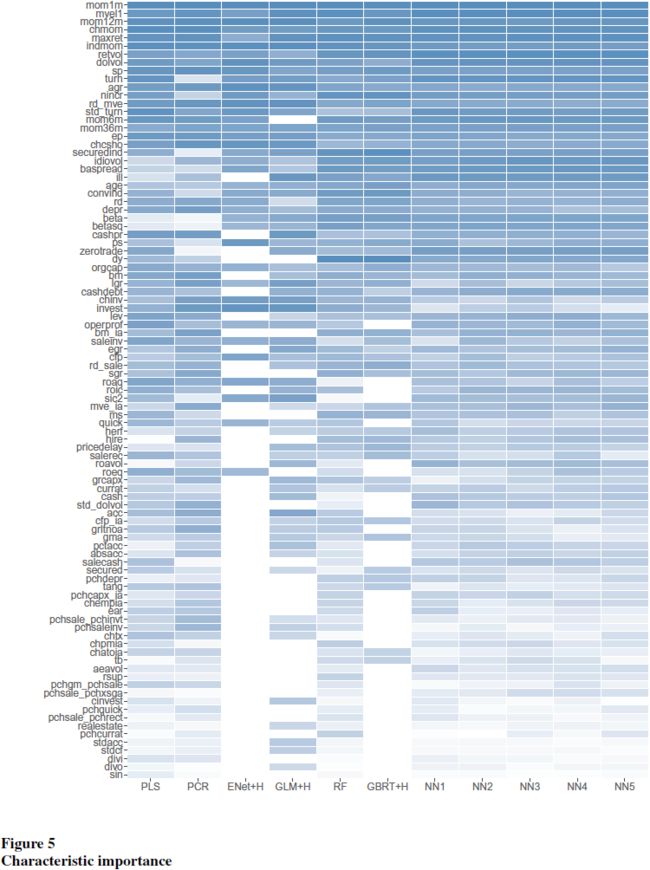
另一种测度是SSD，该文发现结果与 $R^2$ 减少测度相关性极高，在不同模型中，两种测度的 Pearson 相关系数在 84.0%到 97.7%之间。

下图是宏观变量的基于 $R^2$ 减少的重要度：

可以看出在所有模型中总账面市值比（aggregate book-to-market ratio）都非常重要，而市场波动率都不太重要。

将所有特征都变换到(-1,1)区间中，只变动 1 个变量，而固定其他变量都为 0，可以得到不同变量对期望超额收益率的边际影响，结果如下：

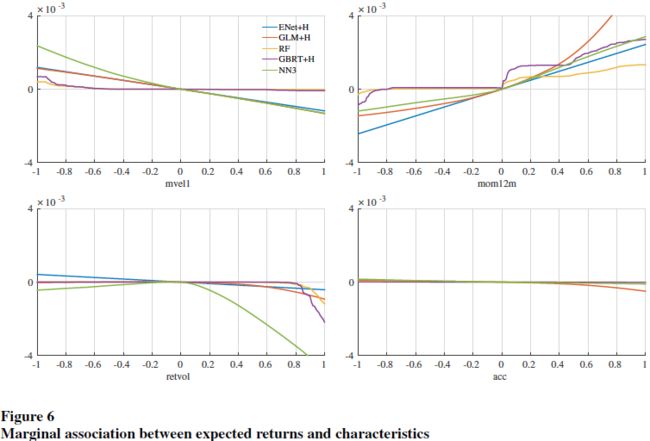
树模型和神经网络模型的优异表现，很可能来自它们捕捉复杂的预测因子的交互作用的能力。下图是在 NN3 模型中，同时变动一对预测因子而固定其他预测因子为 0，检验几对预测因子的交互作用对期望收益率的影响：

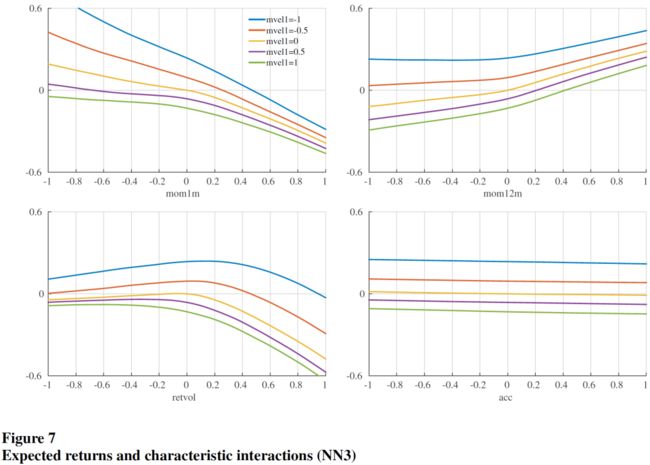
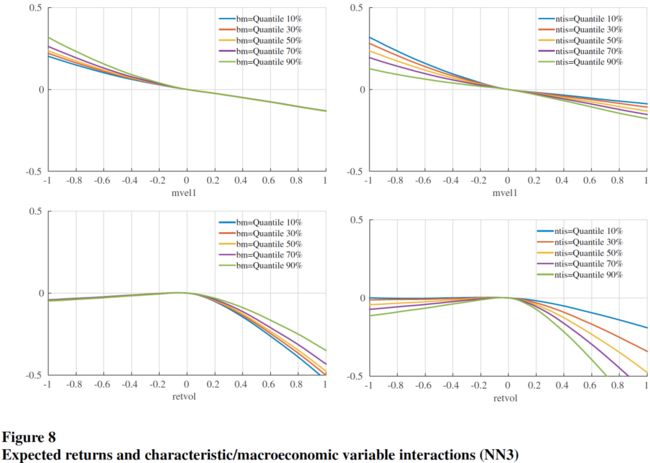
3.4 组合预测

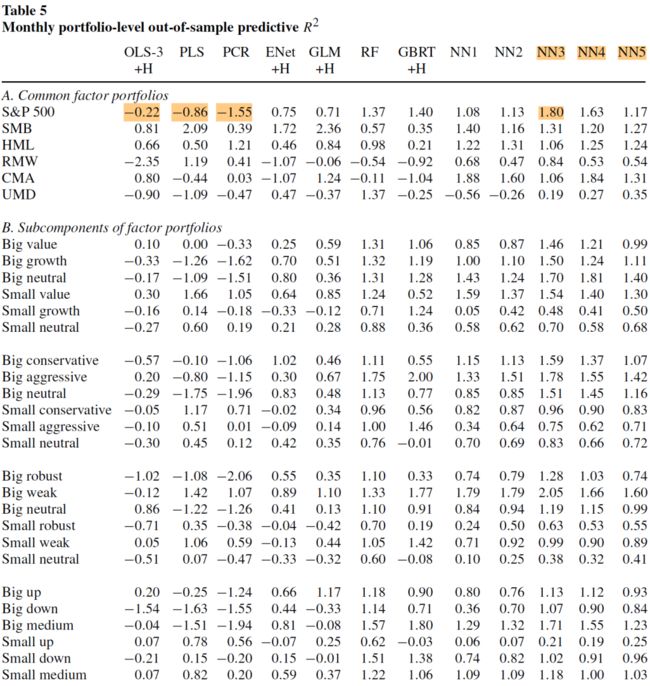
以上都是机器学习对个股的收益率预测，如果将不同股票组成一个投资组合，机器学习能否准确预测组合的收益率？

该文检验了机器学习对 30 个不同的投资组合收益率的预测能力，其中 6 个组合是 S&P 500 组合，以及 Fama French 的规模、价值、盈利、投资、动量组合，这些都构建成零投资的多空组合。对于后面的 4 个组合，再使用市值分别对它们做 $2\times 3$ 划分，构建纯多头组合，最后共形成 30 个投资组合。对于每个投资组合，都用 CRSP 市值加权。

这些投资组合的月度预测 $R^2$ 如下：

Campbell 和 Thompson（2008）指出，$R^2$ 的哪怕是很小的提升，对于均值-方差型投资者也可以获得很大的效用收益，利用预测的信息，主动型投资者可获得比买入并持有型投资者更高的夏普比率。使用他们在同一篇文章中提出的市场择时交易策略，可以看不同的机器学习模型可获得的夏普比率：

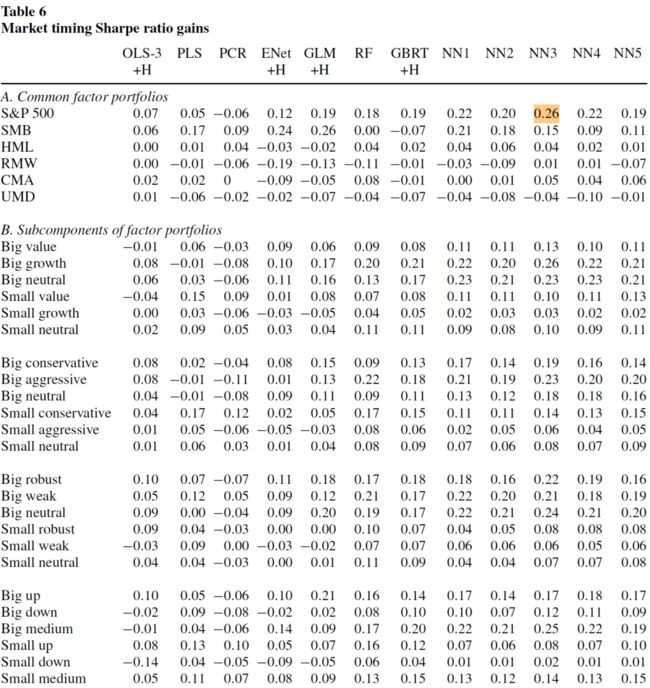
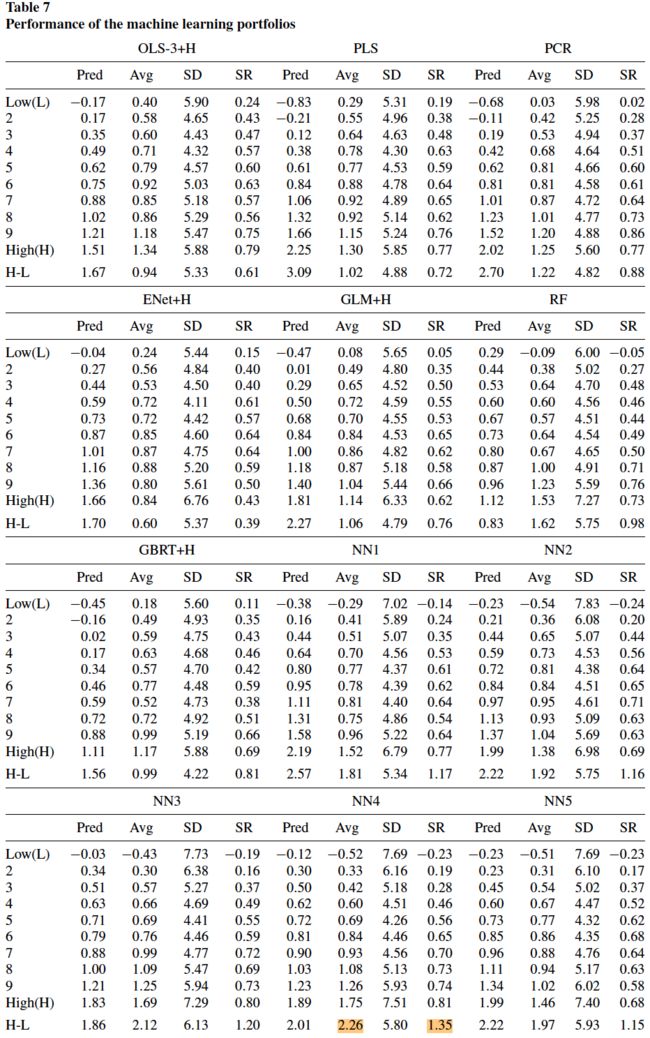
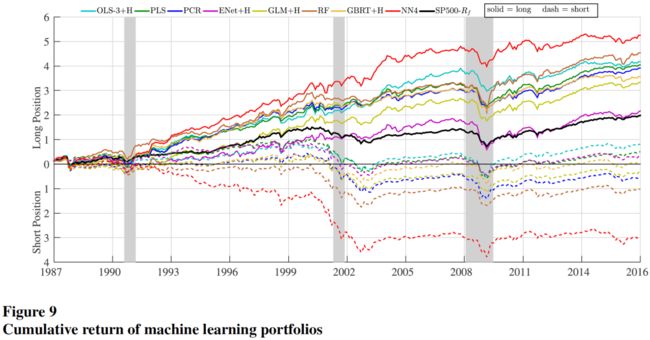
能否直接用机器学习选择股票，构建投资组合，而非对一个既定的投资组合进行预测？本文构造了这样的策略：在每个月末，对每个股票在下个月的收益率作出预测，基于预测对股票排序并分为 10 分位，使用市值加权构造零投资多空组合，即做多预测收益率最高的分位，做空预测收益率最低的分位，在每个月都进行上述操作。

采用不同的机器学习模型，每个分位的多头收益率情况如下：

每种机器学习模型构造的零投资多空组合的最大回撤、最大单月回撤、换手率、平均月收益率、用 FF5 因子和动量因子做风险调整后的 $\alpha$、$\alpha$ 的 t 统计量、FF5 因子和动量因子可解释的 $R^2$、信息比率（IR）情况如下：

将各多空组合的累积收益率可视化：

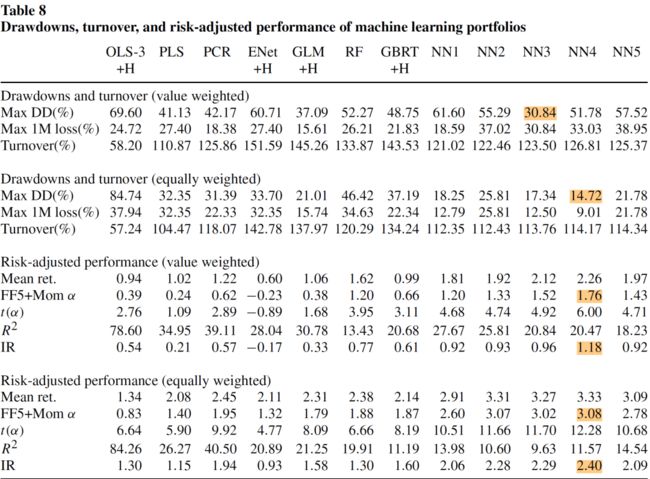
此外，还可以将不同机器学习模型综合使用，有两种方法：

• 将 11 种机器学习模型的多空组合等权重加权；
• 轮换机器学习模型。在每年都利用在验证集数据上的预测 $R^2$，找出最佳的机器学习模型，用它进行下一年的投资，一年后继续重复该过程，再选择一次最佳的机器学习模型。

参考文献

• Gu, Shihao, Bryan Kelly, and Dacheng Xiu. 2020. “Empirical asset pricing via machine learning.” Review of Financial Studies 33(5): 2223-2273.