定义及概念
在一个无向图G中,存在一个点集V,从图G中删掉所有属于V的点及其与之相连的边,G不连通。如果有一个边集E,删掉所有属于这个集合的边,G不连通。
- 点连通度:最小V的点数
- 边连通度:最小E的边数
- 割点:点连通度为1时,V的唯一元素
- 割边(桥):边连通度为1时,E的唯一元素
- 点双连通:任意两点间,存在两条或以上路径,且路径上的点互不重复。(点连通度大于1即可)
- 边双连通:任意两点间,存在两条或以上路径,且路径上的边互不重复。(边连通度大于1即可)
- 双连通分量:在图G中的子图G‘,是一个双连通子图,它不是其他双连通子图的真子集,则它是一个双连通分量。
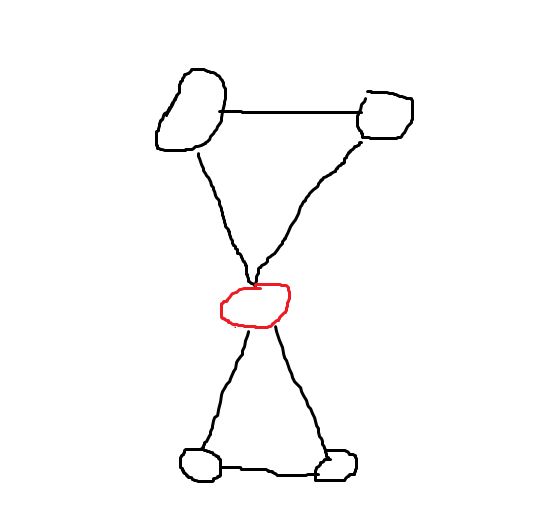
- 边双连通分量一定是点双连通,反之不成立。如下图,不存在割点,即为点双连通,但不是边双连通。
推论
- 有割点不一定有割边
- 有割边不一定有割点
两个割点之间的边不一定是割边
割边的端点不一定是割点
一个图可能有多个割点,有多个桥
tarjan算法
定义
- 树枝边:DFS搜索树上的边
- 前向边:与DFS方向相同的边
- 返祖边:与DFS方向相反的边
割点
- 关于DFS搜索树的根节点,如果它有两棵或两棵以上的子树,则它是割点。
- DFS树不存在横叉边,所以多棵子树不可能通过直接连通。
- 关于其他节点,如果其子孙的返祖边,只能连到自己或自己的子孙,而连不到它的祖先,那此节点为割点。
#include
#include
#include
#define MAXN 100005
int head[MAXN];
struct edge{
int v,next;
}G[MAXN<<1];
int tot = 0;
int dfn[MAXN],low[MAXN],num = 0;
int ans[MAXN];
int N,M;
inline void add(int u,int v){
G[++tot].v = v;G[tot].next = head[u];head[u] = tot;
}
void tarjan(int u,int fa){
dfn[u] = low[u] = ++num;
int count = 0;//统计子树数量
for(register int i=head[u];i;i=G[i].next){
int v = G[i].v;
if(!dfn[v]){
tarjan(v,u);
++count;//子树数量+1
low[u] = std::min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=fa)ans[u] = 1;// 如果u不是根节点
}
low[u] = std::min(low[u],dfn[v]);
}
if(count>=2&&u==fa)ans[u] = 1;//如果u是根节点,且有两个及两个以上的子树
}
int main(){
std::memset(head,0,sizeof(head));
std::memset(ans,0,sizeof(ans));
std::memset(dfn,0,sizeof(dfn));
scanf("%d%d",&N,&M);
int u,v;
for(register int i=1;i<=M;++i){
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
for(register int i=1;i<=N;++i){
if(!dfn[i])tarjan(i,i);
}
int count = 0;
for(register int i=1;i<=N;++i){
if(ans[i])++count;
}
printf("%d\n",count);
for(register int i=1;i<=N;++i){
if(ans[i])printf("%d ",i);
}
return 0;
} 割边
- 返祖边:一定不是割边,删掉此边后不影响图连通。
- 关于一条边(u,v),若此边之下的子树有返祖边,且这条返祖边能回到u的祖先及u,则不是割边