蓝桥杯-剪格子（2013-A-9）

标题：剪格子

如图p1.jpg所示，3 x 3 的格子中填写了一些整数。

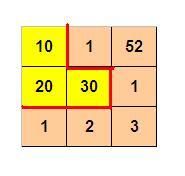
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是60。

本题的要求就是请你编程判定：对给定的m x n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。
如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割，则输出 0

程序输入输出格式要求：
程序先读入两个整数 m n 用空格分割 (m,n<10)
表示表格的宽度和高度
接下来是n行，每行m个正整数，用空格分开。每个整数不大于10000
程序输出：在所有解中，包含左上角的分割区可能包含的最小的格子数目。

例如：
用户输入：
3 3
10 1 52
20 30 1
1 2 3

则程序输出：
3

再例如：
用户输入：
4 3
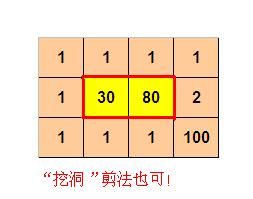
1 1 1 1
1 30 80 2
1 1 1 100

则程序输出：
10

(参见p2.jpg)

资源约定：
峰值内存消耗 < 64M
CPU消耗 < 5000ms

#include 
#include 
#include 
#include 
#define mk(i,j) make_pair(i,j)
using namespace std;

int m, n;
int total;
int g[10][10];
int ans;
/*抽象了一种剪辑方法*/
class Cut {
     
public:
    set<pair<int, int> > grids;//包含若干格子
    int sum;//所有格子的数值的求和
};
/**
 * 将st中的元素拷贝到新set中
 * @param st
 * @return
 */
set<pair<int, int> > copySet(set<pair<int, int> > &st) {
     
    set<pair<int, int> >::iterator iter = st.begin();
    set<pair<int, int> > ans;
    while (iter != st.end()) {
     
//        重新mkpair，加入新set中
        ans.insert(*iter);
        iter++;
    }
    return ans;
}
void add(int sum, int i, int j, set<pair<int, int> > &grids, Cut *&cut_new) {
     
    const pair<int, int> &pair_n = make_pair(i , j);
//                    深度拷贝set
    set<pair<int, int> > grids_copy=copySet(grids);
    grids_copy.insert(pair_n);
    cut_new->grids=grids_copy;
    cut_new->sum=sum+g[i][j];
}
vector<Cut *> vs[100];//分别存储格子数为1~100的各种剪法

int main(int argc, const char *argv[]) {
     
    scanf("%d %d", &m, &n);
    for (int i = 0; i < n; ++i) {
     
        for (int j = 0; j < m; ++j) {
     
            scanf("%d", &g[i][j]);
            total += g[i][j];
        }
    }
//    第一个格子就是一半
    if (g[0][0] == total / 2) {
     
        printf("%d\n", 1);
        return 0;
    }

    /*左上角格子,只有一种剪法，加入v[1]*/
    Cut *c = new Cut();
    const pair<int, int> p = make_pair(0, 0);
    c->grids.insert(p);
    c->sum = g[0][0];
    vs[1].push_back(c);//只包含一个格子且包含00的只有一种剪法

    for (int i = 2; i <= m * n; ++i) {
     
//        i是格子数，用vs[i-1]里面的来生成
//迭代vs[i-1]里面的所有剪法
        for (int j = 0; j < vs[i - 1].size(); ++j) {
     
//            pCut代表一种剪辑方法
            Cut *pCut = vs[i - 1][j];
//            这种剪辑方法里面记录了所有格子，这些格子每个都扩展一个，即形成个数+1的剪法
            set<pair<int, int> > &grids = pCut->grids;
            int sum = pCut->sum;
            set<pair<int, int> >::iterator iter = grids.begin();
//            迭代所有的格子，尝试添加它的邻居
            while (iter != grids.end()) {
     
                const pair<int, int> &p = *iter;//代表一个格子的坐标
                int x=p.first;
                int y=p.second;

                if(x+1<n&&grids.find(mk(x+1,y))==grids.end()){
     //下方，能走通且下方格子不在当前集合中

                    Cut *cut_new=new Cut();//生成一个新的剪法
                    add(sum, x+1, y, grids, cut_new);//将原有的格子全部拷入，再增加当前试探的新的格子
                    if(cut_new->sum==total/2){
     
                        printf("%d\n", i);
                        return 0;
                    }else if(cut_new->sum<total/2)
                        vs[i].push_back(cut_new);
                }
                if(x-1>=0&&grids.find(mk(x-1,y))==grids.end()){
     //上方
                    Cut *cut_new=new Cut();
                    add(sum, x-1, y, grids, cut_new);
                    if(cut_new->sum==total/2){
     
                        printf("%d\n", i);
                        return 0;
                    }else if(cut_new->sum<total/2)
                    vs[i].push_back(cut_new);
                }
                if(y+1<m&&grids.find(mk(x,y+1))==grids.end()){
     //右方
                    Cut *cut_new=new Cut();
                    add(sum, x, y+1, grids, cut_new);
                    if(cut_new->sum==total/2){
     
                        printf("%d\n", i);
                        return 0;
                    } else if(cut_new->sum<total/2)
                    vs[i].push_back(cut_new);
                }
                if(y-1>=0&&grids.find(mk(x,y-1))==grids.end()){
     //左方
                    Cut *cut_new=new Cut();
                    add(sum, x, y-1, grids, cut_new);
                    if(cut_new->sum==total/2){
     
                        printf("%d\n", i);
                        return 0;
                    }else if(cut_new->sum<total/2)
                    vs[i].push_back(cut_new);
                }
                iter++;
            }
        }
    }
    printf("%d\n", 0);
    return 0;
}