ACM有关子序列的DP题合集【plus: Codeforces 597C Subsequences】
最近发现自己在DP方面真的很弱,特别是在处理子序列方面,所以搜集了一些相关题目来深化理解,如果后期遇到还会继续补上。
先是两道入门水题。都是求最大连续子序列和的。
题目一:HDOJ 1003 Max Sum
Max Sum
TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:65536/32768 K (Java/Others)
Total Submission(s): 247787 Accepted Submission(s):58539
Problem Description
Given a sequence a[1],a[2],a[3]......a[n], your job is to calculate the max sum of asub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.
Input
The first line of the input contains an integer T(1<=T<=20) which means thenumber of test cases. Then T lines follow, each line starts with a numberN(1<=N<=100000), then N integers followed(all the integers are between-1000 and 1000).
Output
For each test case, you should output two lines. The first line is "Case#:", # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence,the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases.
Sample Input
2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5
Sample Output
Case 1:
14 1 4
Case 2:
7 1 6
时间复杂度O(n)
#include
#include
#include
#include
#include
#include
using namespace std;
#define mst(a,b) memset((a),(b),sizeof(a))
#define f(i,a,b) for(int i=(a);i<=(b);++i)
#define rush() int T;scanf("%d",&T);while(T--)
typedef long long ll;
const int maxn= 100005;
const ll mod = 1e9+7;
const int INF = 0x3f3f3f3f;
const double eps = 1e-6;
int main()
{
int n,x;
int cas=1;
rush()
{
scanf("%d",&n);
int Max=-INF;
int sum=0;
int start=1,end=1;
int ss,tt;
for(int i=1; i<=n; i++)
{
scanf("%d",&x);
if(sum<0) //如果sum+x0的话,它对于当前的x是有扩大效果的,所以继续加上x
{
sum+=x;
end=i;
}
if(sum>Max) //由于每步都涉及到sum值的更迭,故每个循环都需要更新最大值
{
Max=sum;
ss=start;
tt=end;
}
}
printf("Case %d:\n",cas++);
printf("%d %d %d\n",Max,ss,tt);
if(T!=0) puts("");
}
return 0;
} 下一道题目的思路跟这道题完全一样,不再赘述。
题目二:HDOJ 1231 最大连续子序列
最大连续子序列
TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:65536/32768 K (Java/Others)
Total Submission(s): 32830 Accepted Submission(s): 14773
Problem Description
给定K个整数的序列{ N1,N2, ..., NK },其任意连续子序列可表示为{ Ni,Ni+1, ...,
Nj },其中 1<= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个,
例如给定序列{ -2,11, -4, 13, -5, -2 },其最大连续子序列为{ 11, -4, 13 },最大和
为20。
在今年的数据结构考卷中,要求编写程序得到最大和,现在增加一个要求,即还需要输出该
子序列的第一个和最后一个元素。
Input
测试输入包含若干测试用例,每个测试用例占2行,第1行给出正整数K(< 10000 ),第2行给出K个整数,中间用空格分隔。当K为0时,输入结束,该用例不被处理。
Output
对每个测试用例,在1行里输出最大和、最大连续子序列的第一个和最后一个元
素,中间用空格分隔。如果最大连续子序列不唯一,则输出序号i和j最小的那个(如输入样例的第2、3组)。若所有K个元素都是负数,则定义其最大和为0,输出整个序列的首尾元素。
Sample Input
6
-2 11 -4 13 -5 -2
10
-10 1 2 3 4 -5 -23 3 7 -21
6
5 -8 3 2 5 0
1
10
3
-1 -5 -2
3
-1 0 -2
0
Sample Output
20 11 13
10 1 4
10 3 5
10 10 10
0 -1 -2
0 0 0
Hint
Hint
Huge input, scanf is recommended.
#include
#include
#include
using namespace std;
#define mst(a,b) memset((a),(b),sizeof(a))
#define f(i,a,b) for(int i=(a);i<=(b);++i)
#define rush() int T;scanf("%d",&T);while(T--)
typedef long long ll;
const int maxn= 10005;
const ll mod = 1e9+7;
const int INF = 0x3f3f3f3f;
const double eps = 1e-6;
int a[maxn];
int main()
{
int n;
while(~scanf("%d",&n)&&n)
{
int Max=-INF;
int sum=0;
int start=1,end=1;
int ss,tt;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
if(sum<0)
{
sum=a[i];
start=i;
end=i;
}
else
{
sum+=a[i];
end=i;
}
if(sum>Max)
{
Max=sum;
ss=start;
tt=end;
}
}
if(Max<0)
{
Max=0;
ss=1;
tt=n;
}
printf("%d %d %d\n",Max,a[ss],a[tt]);
}
return 0;
}
题目三:HAUTOJ 1266 最大子段和
最大子段和
TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:65536/65536 K (Java/Others)
Total Submission(s): 305 Accepted Submission(s): 120
Problem Description
一个大小为n的数组a1到an (-10^4≤ai≤10^4)。请你找出一个连续子段,使子段长度为奇数,且子段和最大。
Input
第一行为T(1≤T≤5),代表数据组数。
之后每组数据,第一行为n(1≤n≤10^5),代表数组长度。
之后一行n个数,代表a1到an。
Output
每组数据输出一行,表示满足要求的子段和最大值。
Sample Input
1
4
1 2 3 4
Sample Output
9
就是这么一道看似简单的题,在比赛时卡了我两个多小时QAQ
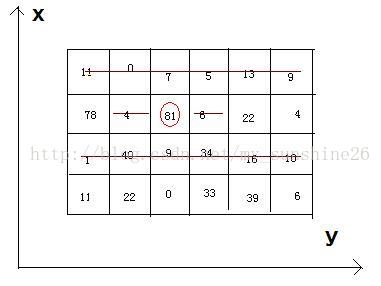
跟前面的题目唯一的变化就是该题要求序列长度必须为奇数。那么我们不妨这样考虑,先取一个值,然后就两个两个数一起取,至于要不要加到sum上去跟上面略有不同,如果sum+a[i]+a[i+1] 另外由于要求是奇数个,所以我们遍历的起点应该有两个:即第一个元素和第二个元素。 个人觉得这道题还是有点价值的,题意是求最大上升子序列,且当长度相同时取取字典序最小的那个,开始套了求最大上升子序列长度的模板,一直WA,而且找不出数据来反驳自己,后来终于发现了问题所在,还是对模板没有理解透啊。 被我注释掉的便是错误做法,虽然能输出最大长度,但序列却不是我们所要求的。(一开始试了很多次,两个结果都是相同的) 后来我终于找到了一组数据,使这种方法结果出错。 10 2 6 8 4 5 6 3 2 1 5 正解: 4 2 4 5 6 错解: 4 1 3 5 6 那么问题出在哪里呢,其实看上面的数据就是到问题所在了,由于在temp数组中每次保存的是当前数据放进相应位置后的结果,这样的话,就会出现一种bug:序号大的数反而可能拍排到序号小的数据前面去了,所以我们需要一个d[i]数组,记录每个数据更新temp数组后所在的位置,然后再逆序遍历即可,很巧妙,建议自己模拟一下。 题目五:HDOJ 2845 Beans TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:32768/32768 K (Java/Others) Problem Description Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with differentqualities beans. Meantime, there is only one bean in any 1*1 grid. Now you wantto eat the beans and collect the qualities, but everyone must obey by thefollowing rules: if you eat the bean at the coordinate(x, y), you can’t eat thebeans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), andthe both rows whose abscissas are x-1 and x+1. Input There are a few cases. In each case, there are two integer M (row number) and N(column number). The next M lines each contain N integers, representing thequalities of the beans. We can make sure that the quality of bean isn't beyond1000, and 1<=M*N<=200000. Output For each case, you just output the MAX qualities you can eat and then get. Sample Input 4 6 11 0 7 5 13 9 78 4 81 6 22 4 1 40 9 34 16 10 11 22 0 33 39 6 Sample Output 242
题意:给出一个n*m的矩阵,你的初始能量值为0,矩阵的每个格点上都有一个值,在上面经过后你会获得格点上数字的值,你看可以从一个地方走到其他任意地方,除了一个限制条件,如果你经过了(i,j)这个点,那么你就不能在去走(i,j-1),(i,j+1)以及第i-1行以及i+1行。问最大可以获得的能量值为多少。 思路:其实你会发现这个限制条件对行和列的限制有异曲同工的意思。我们可以把问题分解首先去求在每一行能获得的能量最大值,用col[i]表示某一行前i个数所能获得的能量最大值,容易写出状态转移方程为 col[i]=max(col[i-1],col[i-2]+mp[i]) 其中mp[i]表示该行第i个数的值。 然后我们用best[i]表示前i行所能获得的最大能量值,跟上面类似,写出状态转移方程 row[i]=max(row[i-2]+mp[i],row[i-1]) 这里的mp[i]表示某一行所能获得能量的最大值。 最终结果即为row[n] TimeLimit: 1000/1000 MS (Java/Others) Memory Limit:32768/32768 K (Java/Others) Problem Description Bruce Force hasgone to Las Vegas, the El Dorado for gamblers. He is interested especially inone betting game, where a machine forms a sequence of n numbers by drawingrandom numbers. Each player should estimate beforehand, how many increasingsubsequences of length k will exist in the sequence of numbers. Input The input contains several test cases. The first line of each test case containstwo numbers n and k (1 ≤ k ≤ n ≤ 100), where n is the length of the sequencedrawn by the machine, and k is the desired length of the increasingsubsequences. The following line contains n pairwise distinct integers ai(-10000 ≤ ai ≤ 10000 ), where ai is the ithnumber in the sequence drawn by the machine. Output For each test case, print one line with the number of increasing subsequences oflength k that the input sequence contains. You may assume that the inputs arechosen in such a way that this number fits into a 64 bit signed integer . Sample Input 10 5 1 2 3 4 5 6 7 8 910 3 2 3 2 1 0 0 Sample Output 252 0 题意:给出一个长度为n的序列,问序列有多少长度为k的单调递增子序列。 分析:我们可以把问题分解,用dp[i][j]表示以num[i]结尾且递增序列长度为j的个数。那么可以写出状态转移方程: dp[i][z]=dp[i][z]+dp[j][z-1] (if(num[i]>num[j])&&(i>j)) 最终结果便是 附:Codeforces 597C Subsequences time limit per test 1second memory limit per test 256megabytes For the given sequence with n different elements find the number ofincreasing subsequences with k + 1 elements. It is guaranteed that theanswer is not greater than 8·1018. Input First line contain two integer values n and k (1 ≤ n ≤ 105, 0 ≤ k ≤ 10) — the length of sequence and the number of elements in increasing subsequences. Next n lines contains one integer ai (1 ≤ ai ≤ n) each — elements of sequence. All values ai are different. Output Print one integer — the answer to the problem. Examples Input 5 2 Output 7 dp[i][j]的含义与上面相同,长度为就且最后一个元素为num[i]的递增序列的种数。状态转移方程也相同。 唯一不同的便是这里可以利用二维树状数组将三维的时间复杂度降为二维。 该题代码中的dp[i][j]=getsum(j-1,num[i]-1)-getsum(j-2,num[i]-1) 与上一题代码中的dp[i][z]=sigma(dp[j][z-1]) (1<=j<=i-1等价) TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:65536/65536 K (Java/Others) Problem Description There is a number sequence A1,A2....An,you can selecta interval [l,r] or not,all the numbers Ai(l≤i≤r) will become f(Ai).f(x)=(1890x+143)mod10007. After that,thesum of n numbers should be as much as possible.What is the maximum sum? Input There are multiple test cases. Output For each test case,output the answer in a line. Sample Input 2 10000 9999 5 1 9999 1 9999 1 Sample Output 19999 22033 题意:有一个长为n的序列,你可以对序列中的任意一个区间进行一个转化(可以不进行操作),区间内的所有数x会变成(1890x+143)mod10007,问经过操作后所有数和的最大值为多少。 思路:乍一看没有任何头绪,但其实可以对其进行一个微妙的转化,我们先算出序列中的每一个数经过操作后与原来数的差值计算出来,然后这些差值求一个最大连续子序列和不就行了。 PS:注意初始化子序列最大和为0(不操作),因为如果最大和小于0,还不如不操作。 TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:65536/65536 K (Java/Others) Problem Description Alice gets two sequences A and B. A easy problem comes. How many pair of sequence A'and sequence B' are same. For example, {1,2} and {1,2} are same. {1,2,4} and{1,4,2} are not same. A' is a subsequence of A. B' is a subsequence of B. Thesubsequnce can be not continuous. For example, {1,1,2} has 7 subsequences{1},{1},{2},{1,1},{1,2},{1,2},{1,1,2}. The answer can be very large. Output theanswer mod 1000000007. Input The input contains multiple test cases. Output For each test case, output the answer mod 1000000007. Sample Input 3 2 1 2 3 2 1 3 2 1 2 3 1 2 Sample Output 2 3 题意:给出两个长度分别为n,m的序列a和b,求它们有多少相同的子序列。(特别注意,这里的子序列跟子集的定义差不多) 思路:用dp[i][j]表示a的前i个元素的子集与b的前j个元素的子集相等的数目,在纸上模拟一下,可以得到状态转移方程: dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1] (if(a[i]!=b[j])) dp[i][j]=dp[i-1][j]+dp[i][j-1] (if(a[i]==b[j])) 第一个方程很好理解,有点容斥的意思,相加之后减去重复的部分。 第二个有点抽象,但可能这样理解会好点,如果a[i]==b[j],那么还比第一种多了什么?首先多了{a[i]},{b[j]},这一个相等的情况,还有一种便是我们可以再dp[i-1][j-1]的所有相同子集地情况中两边加上相等的元素a[i],b[j],那么不还是相等的吗?所以只要在第一个方程的基础上加上(dp[i-1][j-1]+1)即可。 最终结果为dp[n][m]
#include
题目四:UESTC OJ 1006 最大上升子序列 (题目无法复制,直接看链接吧。。。)#include
Beans
Total Submission(s): 4904 Accepted Submission(s): 2288
Now, how much qualities can you eat and then get ?
#include
题目六:HDOJ 2372 El DoradoEl Dorado
Total Submission(s): 581 Accepted Submission(s): 294
Bruce doesn't trust the Casino to count the number of increasing subsequencesof length k correctly. He has asked you if you can solve this problem for him.
The last test case is followed by a line containing two zeros.
#include C. Subsequences
1
2
3
5
4
分析:这道题显然是上面那题的升级版,因为n的数据范围从100,到了100000,如果我们还是按照上面三重循环转移显然会TLE。我们可以考虑用二维的树状数组维护前缀和。#include
题目七:HDOJ 5586 SumSum
Total Submission(s): 1701 Accepted Submission(s): 871
First line of each case contains a single integer n.(1≤n≤105)
Next line contains n integers A1,A2....An.(0≤Ai≤104)
It's guaranteed that ∑n≤106.#include
题目八:HDOJ 5791 TwoTwo
Total Submission(s): 2100 Accepted Submission(s): 921
For each test case, the first line cantains two integers N,M(1≤N,M≤1000). The next linecontains N integers. The next line followed M integers. All integers arebetween 1 and 1000.
#include