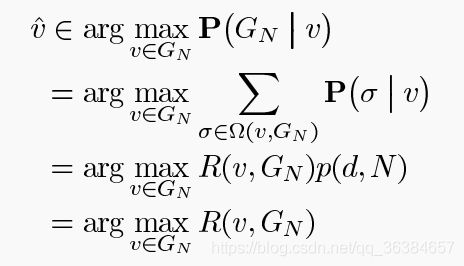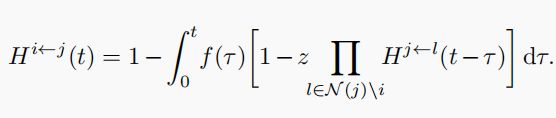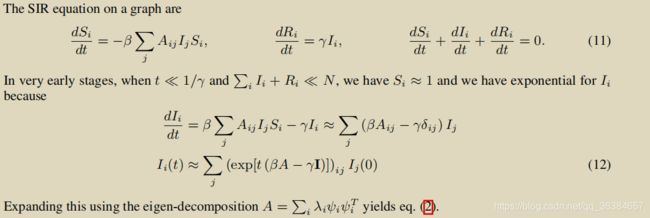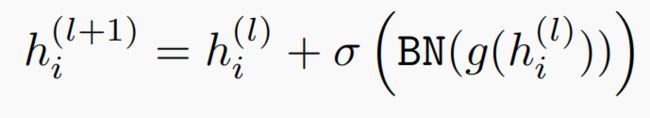复杂网络论文解析——《Finding Patient Zero:Learning Contagion Source with Graph Neural Networks》

 本文为原创，转载需声明出处。

介绍最近看的一篇复杂网络研究流行病传染源的文章，《Finding Patient Zero: LearningContagion Source with Graph Neural Networks》，据作者所述，他们的工作是第一个通过深度学习推断信息源问题并通过真实数据测试验证了结果。文章主要贡献如下：

1.在带有周期的图中找到“零号病人”的准确性具有上限，并且与所使用的推理算法无关。

2.超出一定时间，推理变得困难，强调了快速和早期发现零号病人的重要性。

3.使用GNN预测零号病人在速度和准确性方面优于消息传递算法（DMP）

4.作者使用了广泛的实验对不同的流行病动力学和图结构进行了验证，包括最新的新冠病毒COVID-19的数据。

                                                                          《找到零号患者：使用图神经网络GNN学习传染源》

 一、Finding Patient Zero“追踪零号病人”意义与现状

1.1意义

“零号病人”，指的是第一个患某种传染病，并开始散播病毒的病人。在流行病调查中，通常被叫做首发病例。在传染病的发生发展和传播过程中以及传染病的认知、研究过程中首发病例一直是占有重要的地位，通过对首发病例的细致调查，能为疾病来源、病因分析、预测、控制措施采用、预警机制的建立提供大量宝贵信息。国内研究零号病人称为“信息源推断”。传染病首发病例在流行病学调查中的现实意义 ：

国内的研究

• 1.判断潜伏期

• 2.迅速确定传播方式

• 3.时间效率优势，减少采取防控措施的社会成本

• 4.判定疾病来源

• 5.为试剂和疫苗研发提供样本

传染病流行有三个核心环节:传染源、传播途径和易感人群。但是当前我们普遍采取的隔离措施仅仅是从后面两个环节来切断病毒的传播的，面对传染病如:新型冠状病毒，人群具有普遍的易感性。找到零号病人我们就可以对他及与他有过亲密接触的人进行观察分析，从而得到他们发病的症状以及发病的时间，确认潜伏期，判断出病毒的传播能力。这为病情的预测和预警机制的建立都起到了重要的作用，有了这些数据及资料，我们就可以采取一些对应的措施来严防严控疫情的发展。通过对零号病人的观察及分析，我们可以获得更多与病毒有关的信息，并且对其应用一些治疗药物，查看药物的作用及效果。若零号病人是无症状病毒携带者，我们也可以对其的血液和体液进行进一步的化验，了解他的免疫机制，判断出他是如何将病毒传播给其他人的，者对于后续研制抗病毒的血清、疫苗及药物都有很大的作用。

---

2.现状

为了跟论文一致，下面用P0（patient zero）代替”零号病人“的描述。

参考：

1.追踪“零号病人”

2.病毒学专家：找到“零号病人”到底对防疫有多重要

疾病传播研究通常通过构建人工网络（也叫人工图）模拟病毒传播过程，病毒爆发规模受到网络结构和网络规模的影响。实际的病毒从爆发开始到流行病监测和接触者追踪开始通常会有一个延迟。所以在研究时，我们可能只会在某些中间时间观察图的状态，而无法访问完整的病毒传输链。 由于存在随机性，同一源节点可能导致不同的流行病传播轨迹。此外，从图快照的嘈杂观测中学习P0在计算上是棘手的，并且复杂度随着图的大小呈指数增长。难点总结如下：

• 信息的感染扩散过程中的数据获取不完整；
• 信息源发出信息的时刻未知；
• 感染可能存在随机休眠期，根据节点之间的长度变化（先发病的未必先感染）

由于上述挑战，学习传染过程动力学的大多数工作都集中于推断扩散的正向动力学（ forward dynamics），学习反向动力学（ reverse dynamics）和识别扩散源的问题已被大大忽略。 学习方向动力学的主要有：“rumor centrality” for contagion processes on trees(基于树结构的谣言中心性传播)和Dynamic Message-passing(DMP) on graphs(基于图的动态消息传递（DMP）），但都需要输入传播动力学模拟的参数。

2.1基于谣言中心性方法

 Shah和Zaman在2011年提出了一种基于谣言向心性（Rumor Centrality）【1】的方法来识别单源点。他们假设信息在网络中传播依据SI模型，并且感染时间服从指数分布。通过分析观察到感染图的概率，他们发现信息源具有最多条不同的传播路径去感染网络中所有的已感染节点，并以此提出了谣言向心性，同时证明了谣言向心性是在规则树图下的最大似然检测器，并且可以利用宽度优先搜索生成树将此方法扩展到一般拓扑结构网络中。

核心公式如下，假设v为源节点，感染形成的子图为GN,得到所有从源节点开始的互斥的R(v,GN)感染排列，查找其最大值，即为rumor centrality。

例子：假设某时刻网络感染的子图如上图所示，使用谣言中心性方法推断信息源（初始感染节点）。

源点	互斥的排列	概率
1	{1,2,3,4} {1,2,4,3}	2/12
2	{2,1,3,4} {2,1,4,3} {2,3,1,4} {2,3,4,1} {2,4,1,3} {2,4,3,1}	6/12
3	{3,2,1,4} {3,2,4,1}	2/12
4	{4,2,3,1} {4,2,1,3}	2/12

结果： 对所有节点均进行源点假设，得到的互斥排列中，节点2的数量最多，因此，其传播能力更强，推断其为信息源点。

2.2基于消息传递方法

Lokhov和Mézard提出了一个基于最大似然估计的近似平均场的动态消息传递（Dynamic Message-passing），从消息传递等式出发来计算以某个节点为源点时，观察到某个感染图的后验概率，并选取后验概率最大的点为估计的源点。

消息传递的核心是2010年Newman提出的消息传递方法，它描述了S态节点转为I态的概率与其邻居节点处在I态的概率的关系。传统上我们考虑节点是否被邻居节点感染，只用考虑节点的邻居中有多少个I态个体，每个I态个体感染能力一定。但在消息传递中，邻居节点是否为I态是用概率表示的。消息传递的核心在于它定义了一个节点不被其邻居感染的概率，并基于这个定义能够推出节点任意时刻，节点为S态、I态、R态等的概率。节点的状态得到了，可以进行流行病模拟，求解流行病传播阈值，感染范围，追踪源节点等。

下面以Newman定义的消息传递方法为例介绍。首先定义了函数表示t时刻节点i未被邻居j感染的概率，分为两种情况：1.节点j在t时刻是S态，不能感染i个体；2.节点j在t时刻之前被感染是I态个体，在在t时刻未传染给i。如图所示，+号表示连接两种情况。在两种情况中，要考虑节点j的感染状态，势必要考虑节点j的邻居节点k,q,r对j的影响。类似的我们用节点j在t时刻之间未被感染的概率描述j的邻居k对j的影响，q,r类似。那么我们可以得到的函数表示：

该式子最里面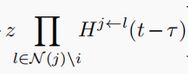表示是节点j不被任何的邻居节点感染，N（j)\i表示节点j除了节点i的所有邻居个体，1-这个式子表示节点j至少被其一个邻居节点感染（即节点j是I态个体的概率），最外层在用1减去，表示节点j未感染到i的概率。消息传递体现在了感染信息由j的邻居（k,q,r等）传递到节点j，再由 节点j传递给节点i，最终计算出节点i的感染概率。

由节点i不被邻居节点j感染的概率可以推出节点i处于S态的概率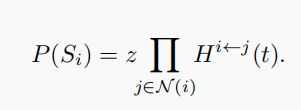，，即i不被它的邻居节点感染的感染。类似的我们可以得到节点处于任意状态的概率。用这个干嘛呢，可以推导流行病传播的阈值，流行病爆发的规模，信息源推断。下面就消息传递用于信息源推断问题进行介绍。

---

Andrey Y Lokhov等在2014年提出了基于消息传递方法的信息源推断。它通过设计一个概率函数P（i|O)表示已知某时刻网络感染状态图，推算信息源为节点i的的概率，这个概率越大，表明i节点是信息源的概率越大。其中O表示网络的感染状态。通过贝叶斯法则，P（i|O)可以用P（O|i)表示，进一步，P（O|i)可以拆分为以i为源点S态的概率，I态概率，R态概率的乘积。通过将P(O|i)映射到函数E(i)=-logP(O|i)中，P(O|i)越大，越接近1,E(i)越接近0，E（i）越小，节点i为感染源的概率越大。这其实是个“放大”函数。

---

在Finding patient zero这篇论文中给出了MP算法流程

输入：演化时间t，以及t时刻网络状态O

输出：假设节点i为信息源节点时最大的概率P(O|i)

1.初始化节点特征和边特征

2.根据流行病的消息传递规则，更新节点的感染状态

3.计算每个节点的为源点时的概率

4.输出最大概率对应的节点

以上两个方法介绍参考了

1.王朝旭. 信息传播网络中信息源推断问题的研究[D].中国科学技术大学,2016. 

2.潘佳纯. 基于非回溯矩阵最大特征值的信息源检测[D].中国科学技术大学,2019.

3.Devavrat Shah and Tauhid Zaman. Rumors in a network: Who’s the culprit? IEEE Transactions on information theory, 57(8):5163–5181, 2011.

4.Andrey Y Lokhov, Marc Mézard, Hiroki Ohta, and Lenka Zdeborová. Inferring the origin of an epidemic with a dynamic message-passing algorithm. Physical Review E, 90(1):012801, 2014.

5.Karrer B and Newman M. E. J. A message passing approach for general epidemic models

 二、基本概念

复杂网络研究流行病传统上使用的蒙特卡洛模拟等方法模拟流行病传播，基于深度学习方法研究流行病的很少，这部分理解起来很吃力。先了解深度学习上的几个概念把，为了方便阅读，我们只需要理解基本思想即可。

提到深度学习，就不得不说神经网络，神经网络其实就是一个输入X到输出Y的映射函数：f(X)=Y，函数的系数就是我们所要训练的网络参数W，只要函数系数确定下来，对于任何输入xi我们就能得到一个与之对应的输出yi，至于yi是否符合我们预期，这就属于如何提高模型性能方面的问题了。

1.正向传播（forward propagation）

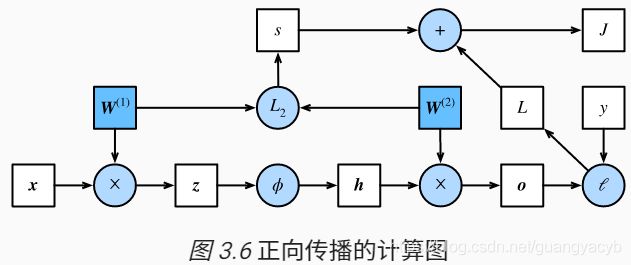
正向传播指对神经网络沿着从输入层到输出层的顺序，依次计算并存储模型的中间变量（包括输出），下图中左下角x为输入，右上角J为输出，方框代表变量，圆圈代表运算符，箭头表示从输入到输出之间的依赖关系。

输入样本为：x∈Rd，不考虑偏差，则中间变量为：

 是隐藏层的权重。将  输入按元素计算的激活函数  ，得到长度为h的向量（隐藏层变量） ，h 也是中间变量。

1：从输入层x开始

2：经过权重参数w偏置参数（b)的处理后再经过一个激活函数处理得到中间隐层1，

3：同理再经过第二个参数处理和激活函数得到中间隐层2

4：最后在通过输出处理得到输出（也就是样本值也成为预测值）J

5：通过定义一个损失函数得到一个损失值

        1）定义损失函数的方式有很多，不同的模型对应的损失函数的方法不同

        2）对于线性回归模型（包括多元线性回归）通用的方法就是最小二乘法

        3）对于分类性问题，一般采用交叉熵的方式

2.反向传播（back-propagation）

反向传播是指计算神经网络参数梯度的方法。依据微积分中的链式法则，沿着从输出层到输入层的顺序，依次计算并存储目标函数有关神经网络各层的中间变量以及参数的梯度。

反向传播的起点就是从loss函数开始的；

通过一个优化器和指定学习率，然后通过最小化损失值来求出最佳的参数

这个就是反向传播的过程了，当然其中一些具体的步骤：包括链式法则，门单元的处理方式（包括，加法，乘法，max等）的处理方式：

其实说白了，反向传播的过程就是一个求偏导数（其实就是求导，就是除了未知量，其他都是常数）的过程，如果有激活函数

激活函数也要求导。

用知乎的例子描述一下正向传播和反向传播的关系：如何理解深度学习中的迭代，正向传播，反向传播？

你拿一根棍子，去掏远处的东西，你随机握住棍子某处，往前伸，去勾东西---正向

伸过去后，你发现棍子距离物品还有点距离，你根据距离，调整了握棍子手的位置--反向

经过一次次伸过去， 一次次调整， 你终于够到东西了(理想情况) ---模型训练结束

参考：

1.详解神经网络的前向传播和反向传播（从头推导）

2.前向传播和反向传播（以简单神经网络为例）

3.GNN图神经网络

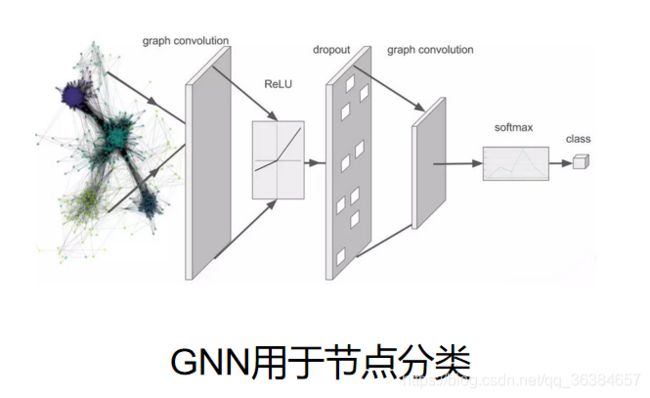
图神经网络 (GNN) 是一种连接模型，它通过图的节点之间的消息传递来捕捉图的依赖关系，图神经网络是一种直接在图结构上运行的神经网络。与标准神经网络不同的是，图神经网络保留了一种状态，可以表示来自其邻域的具有任意深度的信息。虽然发现原始的 GNN 很难为一个固定点进行训练，但是网络结构、优化技术和并行计算的最新进展使它们能够成功地学习。GNN 的一个典型应用是节点分类。本质上，图中的每个节点都与一个标签相关联，我们的目的是预测没有 ground-truth 的节点的标签。图神经网络（GNN）是在图域上运行的基于深度学习的方法。GNN 以其令人信服的性能和较高的可解释性，近年来已成为一种广泛应用的图论分析方法。

图神经网络（GNN）参考了卷积神经网络（CNN）的思想，CNN是用于图像的分类预测任务，图像上的元素是规则的像素点排列 ，可以用一个卷积核矩阵滑动通过对邻居信息的加权求和来更新带求点的值。而graph是不规则的拓扑结构，不能用统一的矩阵进行卷积操作，它参考了傅里叶函数在频域上的展开：函数可以拆成若干子函数相乘的形式，如h(x)=f(x)*g(x)。通过设置一个函数提取graph上的节点邻居信息，完成节点的更新。GNN也是通过多层网络完成最后的输出，前一层的输出作为下一次节点特征的输入。输入层节点的特征是节点的属性，如one-hot编码后的向量。GNN的输出是由要学习的内容的决定的。

三、传播模型

3.1.SIR模型

经典的SIR模型是一种发明于上个世纪早期的经典传染病模型，此模型能够较为粗略地展示出一种传染病的发病到结束的过程，在SIR模型中，将人群分为三个部分：

S：Susceptible，易感者
        I：Infective，感染者

R：Removal，移除者

易感染该疾病的易感人群（S）； 感染了该疾病并具有传染性的感染者（I）； 经历了整个感染期后被恢复的个体（R）。

3.1.1SIR模型演化规则：

S态个体接触I态以beta概率转换为I态个体，而I态个体以gamma概率恢复为R态个体

3.1.2SIR模型动力学方程

公式1描述了S态个体、R态个体、I态个体随时间变化的函数关系：

其中：，表示是S、I、R个体所在的比例之和为1。

Aij表示图的邻接矩阵，Aij=1表示节点i和节点j存在连边即存在接触关系；Aij=0表示节点i和j不连接。

左边表示S态个体随时间减小的量=sum_所有的j个体（S态个体数量比例*是否接触（0、1）*I态个体数量比例*转换概率beta ）

中间表示R态个体增加的量，有I态个体以gamma的概率转换而来

最后表示三者中每个部分都有可能变化，但网络整体的人数并没有改变。（这里一般指的是不考虑人口的出生和死亡）

3.2.SEIR模型

实际情况更加复杂，易感染人群在一开始会经历潜伏期，一段时间之后才出现症状，因此我们在SIR模型的基础上引入潜伏者(The Exposed)，潜伏者按照概率 alpha 转化为感染者。

SEIR演化规则图：

针对SIR模型和SEIR模型，作者分别从连续过程和离散过程进行了传染病动力学分析。主要分析S态、E态、I态和R态之间的相互转换。

3.3.连续过程（Continuous time model）

 作者认为在流行病开始的早期，易感个体概率近似为1，即网络中基本为易感个体，感染和恢复的个体很少。结合SIR演化规则 ，推演出流行病早期节点i为I态个体随时间的函数：

 

 这里是为了给出节点初始时刻S态、I态、R态的概率，为了给MP算法赋值

3.4离散过程（Discrete time model）

 离散过程用概率函数来描述，左边表示t时刻节点为S态，下一时刻为I态的概率；右侧表示t时刻节点为I态，下一时刻为R态的概率，参考SIR状态之间的转换，很容易理解。不在细说。

SIR模型没有考虑个体被感染但没有传染性的情况，即病毒传播具有潜伏期 ，考虑潜伏期时S态和IE态以及E态和I态的转换概率如下：

四、使用GNN追踪信息源

关于GNN的怎么进行信息源推断的，文章说的不是很清楚，对这方面不太了解。欢迎评论补充，介绍这篇文章主要讲一下信息源推断的背景知识。

GNN在处理信息源推断问题上，是先设置一个感染态节点P0，根据网络结构以及SIR或SIER传播规则进行流行病演化，最后得到若干感染状态图，对若干感染状态图划分为训练-测试-验证集。通过训练集得到训练好的模型参数。在用测试和验证集进行实际的信息源推断。计算模型的准确率等。

输入：

输出：

yi表示节点i为P0的概率。

隐藏层

模型超参数选取

 作者对比了经典的 DMP算法进行信息源推断。采用了几种GCN的变体：GCN-S和GAT等

作者发现，采用GNN类的深度学习方法在识别准确率以及时间上花费很低。DMP算法需要14-70多个小时，而深度学习只需几秒，当然深度学习也付出了训练的代价和内存资源的代价。

此外，作者还用对COV I D-2019新冠病毒进行了推断，其选择的是Boston波斯顿的城市的两周内感染状态，为了计算方便，其选取了部分感染子图对其进行信息源推断。其中graph的邻居节点信息的获取是由定位系统计算而来。

 总结：作者通过GNN方法推断信息源问题是基于静态的感染图的推导，网络的拓扑结构不能变化。而实际上网络的拓扑结构是动态变化的，国内外学者在讨论信息源问题的时候很少考虑到网络结构的演化对推断信息源的影响。因此，如何在时序网络上进行信息源推断？需要借助“基于谣言中心性”方法和基于消息传播“的方法来做进一步的研究。GNN提高了推理的速度，但是在可解释性上仍然很难做到。

这只是我个人的一点思考，欢迎各位同学补充。