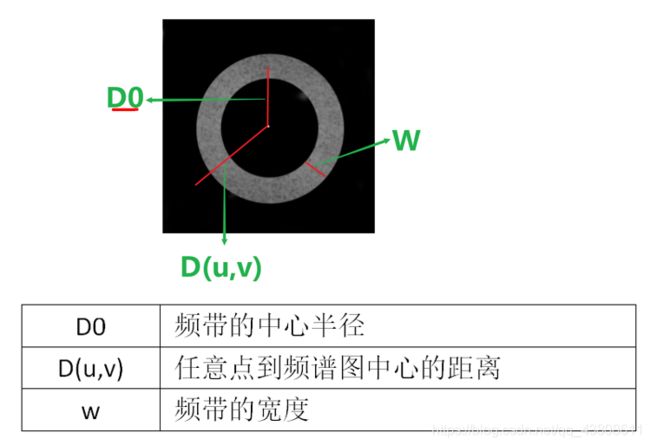
数字图像处理与python实现-带通滤波器

带通滤波器

• 概念
  允许带内频率对应像素的灰度值通过而阻止带外的

• 公式
  

• 公式中的符号含义
  

• 实验流程转换图
  

• 理想带通滤波器代码

#导入工具包
import cv2
import numpy as np
import math
from matplotlib import pyplot as plt

# 读取图像
img = cv2.imread('C:/Users/lenovo/Desktop/lena.jpg', 0)#0的含义:将图像转化为单通道灰度图像

def ideal_bandpass_filter(img,D0,w):
    img_float32 = np.float32(img)#转换为np.float32格式，这是oppencv官方要求，咱们必须这么做
    dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)#傅里叶变换,得到频谱图
    dft_shift = np.fft.fftshift(dft)#将频谱图低频部分转到中间位置，三维(263,263,2)
    rows, cols = img.shape #得到每一维度的数量
    crow, ccol = int(rows / 2), int(cols / 2)  # 中心位置
    mask = np.ones((rows, cols,2), np.uint8)  #对滤波器初始化，长宽和上面图像的一样
    for i in range(0, rows): #遍历图像上所有的点
        for j in range(0, cols):
            d = math.sqrt(pow(i - crow, 2) + pow(j - ccol, 2)) # 计算(i, j)到中心点的距离
            if D0 - w / 2 < d < D0 + w / 2:
                mask[i, j,0]=mask[i,j,1] = 1
            else:
                mask[i, j,0]=mask[i,j,1] = 0
    f = dft_shift * mask  # 滤波器和频谱图像结合到一起，是1的就保留下来，是0的就全部过滤掉
    ishift = np.fft.ifftshift(f) #上面处理完后，低频部分在中间，所以傅里叶逆变换之前还需要将频谱图低频部分移到左上角
    iimg = cv2.idft(ishift) #傅里叶逆变换
    res = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1]) #结果还不能看，因为逆变换后的是实部和虚部的双通道的一个结果，这东西还不是一个图像，为了让它显示出来我们还需要对实部和虚部进行一下处理才可以
    return res

new_image1=ideal_bandpass_filter(img,D0=6,w=10)
new_image2=ideal_bandpass_filter(img,D0=15,w=10)
new_image3=ideal_bandpass_filter(img,D0=25,w=10)

# 显示原始图像和带通滤波处理图像
title=['Source Image','D0=6','D0=15','D0=25']
images=[img,new_image1,new_image2,new_image3]
for i in np.arange(4):
    plt.subplot(2,2,i+1),plt.imshow(images[i],'gray')
    plt.title(title[i])
    plt.xticks([]),plt.yticks([])
plt.show()

• 巴特沃斯带通滤波器代码

#导入工具包
import cv2
import numpy as np
from matplotlib import pyplot as plt

#滤波器
def butterworth_bandstop_kernel(img,D0,W,n=1):
    assert img.ndim == 2
    r,c = img.shape[1],img.shape[0]
    u = np.arange(r)
    v = np.arange(c)
    u, v = np.meshgrid(u, v) #生成网络点坐标矩阵
    low_pass = np.sqrt( (u-r/2)**2 + (v-c/2)**2 ) #相当于公式里的D(u,v),距频谱图矩阵中中心的距离
    kernel = 1-(1/(1+((low_pass*W)/(low_pass**2-D0**2))**(2*n))) #变换公式
    return kernel

def butterworth_bandpass_filter(img,D0,W,n):
    assert img.ndim == 2
    kernel = butterworth_bandstop_kernel(img,D0,W,n)  #得到滤波器
    gray = np.float64(img)  #将灰度图片转换为opencv官方规定的格式
    gray_fft = np.fft.fft2(gray) #傅里叶变换
    gray_fftshift = np.fft.fftshift(gray_fft) #将频谱图低频部分转到中间位置
    #dst = np.zeros_like(gray_fftshift)
    dst_filtered = kernel * gray_fftshift #频谱图和滤波器相乘得到新的频谱图
    dst_ifftshift = np.fft.ifftshift(dst_filtered) #将频谱图的中心移到左上方
    dst_ifft = np.fft.ifft2(dst_ifftshift) #傅里叶逆变换
    dst = np.abs(np.real(dst_ifft))
    dst = np.clip(dst,0,255)
    return np.uint8(dst)

#读取图像
img = cv2.imread('C:/Users/lenovo/Desktop/lena.jpg', 0)

#得到处理后的图像
new_image1=butterworth_bandpass_filter(img,D0=6,W=10,n=1)
new_image2=butterworth_bandpass_filter(img,D0=15,W=10,n=1)
new_image3=butterworth_bandpass_filter(img,D0=25,W=10,n=1)

# 显示原始图像和带通滤波处理后的图像
title=['Source Image','D0=6','D0=15','D0=25']
images=[img,new_image1,new_image2,new_image3]
for i in np.arange(4):
    plt.subplot(2,2,i+1),plt.imshow(images[i],'gray')
    plt.title(title[i])
    plt.xticks([]),plt.yticks([])
plt.show()

• 高斯带通滤波器代码

#导入工具包
import cv2
import numpy as np
from matplotlib import pyplot as plt

def gaussian_bandstop_kernel(img,D0,W):
    assert img.ndim == 2
    r,c = img.shape[1],img.shape[0]
    u = np.arange(r)
    v = np.arange(c)
    u, v = np.meshgrid(u, v)
    low_pass = np.sqrt( (u-r/2)**2 + (v-c/2)**2 )
    kernel = 1.0 - np.exp(-0.5 * (((low_pass ** 2 - D0**2) / (low_pass *W + 1.0e-5))**2))
    return kernel

def gaussian_bandpass_filter(img,D0=5,W=10):
    assert img.ndim == 2
    kernel = 1.0 - gaussian_bandstop_kernel(img,D0,W)
    gray = np.float64(img)
    gray_fft = np.fft.fft2(gray)
    gray_fftshift = np.fft.fftshift(gray_fft)
    dst = np.zeros_like(gray_fftshift)
    dst_filtered = kernel * gray_fftshift
    dst_ifftshift = np.fft.ifftshift(dst_filtered)
    dst_ifft = np.fft.ifft2(dst_ifftshift)
    dst = np.abs(np.real(dst_ifft))
    dst = np.clip(dst,0,255)
    return np.uint8(dst)


#读取图像
img = cv2.imread('C:/Users/lenovo/Desktop/4.png', 0)

new_image1=gaussian_bandpass_filter(img,D0=6,W=10)
new_image2=gaussian_bandpass_filter(img,D0=15,W=10)
new_image3=gaussian_bandpass_filter(img,D0=25,W=10)

# 显示原始图像和带通滤波处理图像
title=['Source Image','D0=6','D0=15','D0=25']
images=[img,new_image1,new_image2,new_image3]
for i in np.arange(4):
    plt.subplot(2,2,i+1),plt.imshow(images[i],'gray')
    plt.title(title[i])
    plt.xticks([]),plt.yticks([])
plt.show()

• 实验结果
  处理正常图像
  
  处理噪声图像
  
• 实验结论
  1、不可以直接使用带通滤波器，如果直接使用会损失大量图像细节
  2、可使用带通滤波器提取噪声模式