Event-B建模实际操作:控制桥上的汽车(三)
接上节;在现在的形式中,桥的模型看起来有些奇妙。按照我们的观察,好像汽车司机能统计汽车的数量,并据此决定能不能从大陆上桥或者从岛上桥。这也意味着我们能看到系统的状态。显然,这是根本不可能的。为此,我们进一步做精化。
Second Refinement: Introducing the Traffic Lights
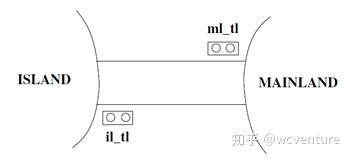
In its present form, the model of the bridge appears to be a bit magic. It seems, from our observation, that car drivers can count cars and thus decide to enter into the bridge from the mainland (event ML_out) or from the island (event IL_out). This means they can observe the state of the system. Clearly, this is not realistic. In reality, as we know, the drivers follow the indication of some traffic lights, they clearly do not count the cars! This refinement then consists of introducing first the two traffic lights, named ml_tl and il_tl, then the corresponding invariants, and finally some new events that can change the colors of the traffic lights. Fig. 37 illustrates the new physical situation which can be observed in this refinement.
Fig. 37. The Traffic Lights
Firstly, create a new Event-B Component. Either use File à New à Event-B Component or right-click on the newly created project and select New à Event-B Component. Use COLOR as the component name, select Context as component-type, and click Finish. Then, add a carrier set and two constants into the context COLOR. The step is shown in Fig. 38.
Fig. 38. Add Carrier Set and Constants
We must extend our set of constants by first introducing the set COLOR and its two distinct values red and green. And we can also claim that Color = {green, red} and green ≠ red. The built context can be seen as Fig. 39.
Fig. 39. Context COLOR
After adding a new context file. We can refine the machine. Create a refinement is by right-clicking on the machine m1 in the project browser and selecting Refine. This will create a “stub” consisting of all variables and events. Here I create a machine with the name m2. We also need to add the relationship between machine file and context file, and connect machine file m2 to context file COLOR, as shown in Fig. 40.
Fig. 40. Connect machine file m2 to context file cd and COLOR
Two new variables are then introduced, namely ml_tl (for mainland traffic light) and il_tl (for island traffic light). These variables are defined as colors: this is formalized in invariants named inv1 and inv2 below. Since drivers are allowed to pass only when traffic lights are green, we better ensure, by two conditional invariants named inv3 and inv4, that when ml_tl is green then the abstract guard of event ML_out holds, and that when il_tl is green then the abstract guard of event IL_out holds. Notice that we are here taking account of requirements ENV-1, ENV-2, and ENV-3. Here are the refined variables, which shown in Fig. 41.
Fig. 41. inv1, inv2 and inv3
Events ML_out and IL_out are now refined by changing their guards to the test of the green value of the corresponding traffic lights. This is here where we implicitly assume that drivers obey the traffic lights, as indicated by requirements ENV-3. Note that events IL_in (entering the island from the bridge) and ML_in (entering the mainland from the bridge) are not modified in this refinement. Here is the new version of event ML_out, which shown in Fig. 42.
Fig. 42. The new version of event ML_out
Here is the new version of event IL_out, which shown in Fig. 43.
Fig. 43. New Version of Event ML_out
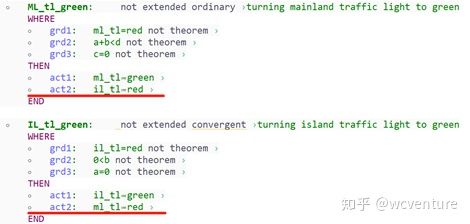
We have to introduce two new events to turn the value of the traffic lights color to green when they are
red and the conditions are appropriate. The appropriate conditions are exactly the guards of the abstract
events ML_out and IL_out. Here are the proposed new events, as shown in Fig. 44.
Fig. 44. New Event ML_tl_green and IL_tl_green
However, inv3 requires ml_tl=green ⇒ c=0 ∧ a+b+c
Fig. 45. Current Proof Obligations View
What remains to be done are the proofs obtained by applying proof obligation rule INV to events IL_out and ML_out. We shall see below that this raises some difficulties.
However, this is an obvious fact that both lights cannot be green at the same time. We thus now introduce it as an additional invariant inv5:
inv5: il_tl=red ∨ ml_tl=red
We note that this invariant could have been a requirement, although it could have been deduced from requirement ENV-3 which says that "cars are not supposed to pass on a red traffic light, only a green one", and requirement FUN-3 which says that " the bridge is one-way or the other, not both at the same time".
Modifying events ML_tl_green and IL_tl_green. This new invariant inv5 has to be preserved and this is clearly not the case with the new events ML_tl_green and IL_tl_green we proposed earlier in Fig. 37, unless we correct them by turning to red the other traffic light, yielding the new action shown in Fig. 46:
Fig. 46. Modifying New Event ML_tl_green and IL_tl_green
Proving that event ML_out preserves invariant inv3. When trying to prove the preservation of invariant
inv3 by event ML_out, we are again in trouble.
Fig. 47. The Proof Tree
As can be seen, the first of the last two sequents cannot be proved when a + 1 + b is equal to d unless
ml_tl is set to red. In fact, when a + 1 + b is equal to d, it means that the entering car is the last one allowed to enter at this stage because more cars would violate requirement FUN-3, which says that there are no more than d cars in the island and bridge. This indicates that event ML_out has to be split into two events (both refining their abstraction, however) as in Fig. 48.
Fig. 48. Split ML_out into two events
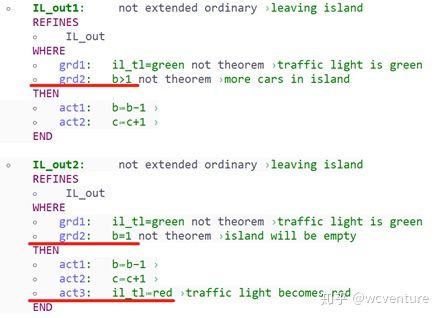
Proving that event IL_out preserves invariant inv4. For similar reasons, invariant inv4 cannot be maintained by event IL_out when b is equal to 1. In this case, the last car is leaving the island. As a consequence, the island traffic light has to turn red. As for event ML_out in the previous section, we have to split event IL_out as in Fig. 49.
Fig. 49. Split IL_out into two events
We have now to prove that the new events cannot diverge. For this, we must exhibit a certain variant that must be decreased by the new events. In fact, it turns out to be impossible. For instance, when a and c are both equal to 0, meaning that there is no car on the bridge in either direction, then the traffic lights could freely change color forever as one can figure out by looking at the new events ML_tl_green and IL_tl_green, as shown in Fig. 50.
Fig. 50. We need to prove that the new events cannot diverge
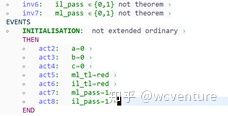
What could then happen is that the light colors are changing so rapidly that the drivers can never pass. We have to make the color changing in a more disciplined way, that is only when some car has passed in the other direction. For this, we introduce two more variables ml_pass and il_pass. Each of them can take two values TRUE or FALSE, they are members of the pre-defined set BOOL made of the two distinct values TRUE and FALSE. When ml_pass is equal to TRUE, it means that one car at least has passed on the bridge going to the island since the mainland traffic light last turned green. And similarly, when il_pass is equal to TRUE. These variables are formalized in the following invariants shown in Fig. 51.
Fig. 51. Adding new variables il_pass and ml_pass
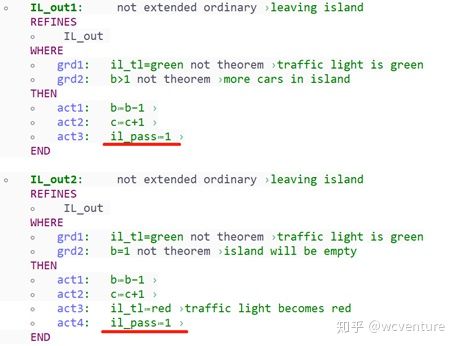
We must now modify events ML_out_1, ML_out_2, IL_out_1, and IL_out_2 to set ml_pass or il_pass to TRUE since a car has passed in the proper direction.
Fig. 52. Modify events ML_out1, ML_out2 to set ml_pass or il_pass
Fig. 53. Modify events IL_out1, IL_out2 to set ml_pass or il_pass
But we must also modify event ML_tl_green and IL_tl_green to reset ml_pass and il_pass to FALSE and also add in their guards the conditions il_pass = TRUE and ml_pass = TRUE respectively in order to be sure that indeed a car has passed in the other direction. This yields the code shown in Fig. 54.
Fig. 54. Modify events ML_tl_green, IL_tl_green to set ml_pass or il_pass
Having done all that, we can now state what is to be proved in order to guarantee that there is no divergence of the new events.
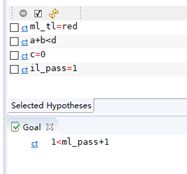
This variant to be proved by applying proof obligation rule VAR on events ML_tl_green and IL_tl_green. However, it cannot prove 1 < ml_pass +1, as shown if Fig. 55.
Fig. 55. Proof obligation “ML_tl_green/VAR”
At this point, we figure out that it cannot be proved unless ml_pass = 1 in the first case (so that ml_pass is equal to 1) and il_pass = 1 in the second one for a similar reason. This suggests adding the following invariants:
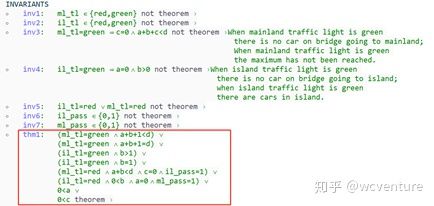
It remains now to prove that the relative deadlock freedom, so we add thm1, as shown in Fig. 56. We have thus to prove that the disjunction of the abstract guards implies the disjunction of the concrete guards.
Fig. 56. pass or il_pass
This example is very similar to the example we introduced earlier in Fig. 35. We can decompose c∈ℕ into c>0 and c=0; a∈ℕ into a>0 and a=0; b∈ℕ into b>0 and b=0. Make sure you finished following task: (1) Type c=0 into the Proof Control View and press the
![]()
button. The proof is split into two branches. One is c=0, another is c>0. (2) Type a=0 into the Proof Control View and press the
![]()
button. (3) Type b=0 into the Proof Control View and press the
![]()
button. Then press the ‘pp’ button for each goal, and press the ‘save’ button. We can see that each goal is indicated by a green mark
![]()
now, as shown in Fig. 57.
Fig. 57. Current Proof Obligation
As a whole, the second refined model (context + machine) design by Rodin is shown as follows.
Context COLOR (final version):
CONTEXT
COLOR ›
SETS
⚬ Color ›
CONSTANTS
⚬ green ›
⚬ red ›
AXIOMS
⚬ axm1: green ∈ Color not theorem ›
⚬ axm2: red ∈ Color not theorem ›
⚬ axm3: green ≠ red not theorem ›
⚬ axm4: Color = {green,red} not theorem ›
END
Machine m2 (final version):
MACHINE
m2 ›
REFINES
⚬ m1
SEES
⚬ cd
⚬ COLOR
VARIABLES
⚬ a ›as in previous abstaction
⚬ b ›as in previous abstraction
⚬ c ›as in previous abstraction
⚬ ml_tl ›mainland traffic light
⚬ il_tl ›island traffic light
⚬ il_pass ›technical boolean
⚬ ml_pass ›technical boolean
INVARIANTS
⚬ inv1: ml_tl ∈ {red,green} not theorem ›
⚬ inv2: il_tl ∈ {red,green} not theorem ›
⚬ inv3: ml_tl=green ⇒ c=0 not theorem ›
When mainland traffic light is green
there is no car on bridge going to mainland
⚬ inv12: ml_tl=green ⇒ a+b+c When mainland traffic light is green the maximum has not been reached ⚬ inv4: il_tl=green ⇒ a=0 not theorem › When island traffic light is green there is no car on bridge going to island ⚬ inv11: il_tl=green ⇒ b>0 not theorem › when island traffic light is green there are cars in island ⚬ inv6: il_pass ∈ {0,1} not theorem › ⚬ inv7: ml_pass ∈ {0,1} not theorem › ⚬ inv8: ml_tl=red ⇒ ml_pass=1 not theorem › ⚬ inv9: il_tl=red ⇒ il_pass=1 not theorem › ⚬ inv5: il_tl=red ∨ ml_tl=red not theorem › ⚬ thm2: 0≥a ⇒ a=0 theorem › ⚬ thm3: 0≥b ⇒ b=0 theorem › ⚬ thm4: 0≥c ⇒ c=0 theorem › ⚬ thm5: ¬ (d≤0) theorem › ⚬ thm6: b+1≥d ∧ ¬(b+1=d) ⇒ ¬(b ⚬ thm7: b≤1 ∧ ¬(b=1) ⇒ ¬(b>0) theorem ›