目录:
1、问题描述
2、Simple Local Search
3、Tabu Search
4、Hybrid Evolutionary Algorithm
5、总结
【注】本文源码仅供参考。
1、问题描述
给定一个无向图G = (V,E),其中V为顶点集合,E为边集合,图染色/图着色问题(graph coloring problem, GCP)是将每个顶点涂上颜色,使得每个相邻的顶点着不同的颜色,求出最少使用的颜色数K。
直接求取最小的颜色数K,是一个NP-hard问题。将问题转化,对应于一个颜色数K,是否存在某种着色方案,使相邻两个节点颜色不同,是一个NP-complete问题,然后将逐渐的减小K。这样两个问题就等效了,我们称后者为 K-coloring 问题。
K-coloring问题定义为:对于一个集合 S = {V1,V2,...,VK},其中 Vi 为所用颜色为 i 的顶点的集合,其中 1≤i≤K。若所有Vi为独立集,则S为一个合法解,否则为一个非法解或者冲突解。任何两个独立集,互换颜色,都不影响冲突数目。
将目标函数定义为冲突数:
满足:
对于所有的合法解,f(S) = 0。
2、Simple Local Search
对于一个K-coloring问题,作如下说明:
1、初始化解。可以选择:为每个顶点从1到K中随机的产生一个颜色;也可以通过某些启发式的方法产生初始解。但是对于一个好的局部搜索算法对初始解应该不敏感,本文算法中采用随机产生初始解
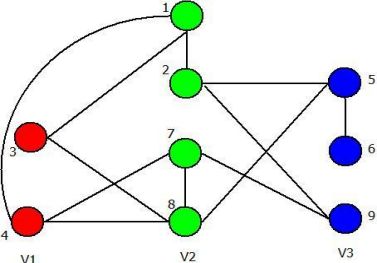
2、定义邻域动作。本文算法中,定义为:对于每一个产生冲突的顶点,令其颜色等于其它K - 1个颜色。邻域大小 = 冲突的顶点数 * (K -1) 。如下图:
对于上图K=3的情况,冲突对为(1,3),(1,4),(7,8),(5,6),冲突边为4条,f(S) = 4,一共七个冲突顶点,每个冲突顶点可以着其它的2中颜色,邻域大小7*2=14。
3、定义Adjacent-Color Table。M[N][K],其中N为顶点总数。M[u][i]其值的意思为,当顶点 u 着颜色 i 时,顶点 u 对应的冲突数。上图的Adjacent-Color Table如下:
当顶点 u ,由颜色 i 变为颜色 j 时,定义这个动作为move(u,i,j),称之为:critical one-moves。Δ(u,i,j) = M[u][j] - M[u][i];对于目标函数值将变为 f' = f + Δ(u,i,j),例如:我们将1号顶点由红色(1)变为绿色(2)时,f'(S) = f(S) + Δ(u,i,j) = 4+1-2=3。如下图所示:
4、更新Adjacent-Color Table。最终确定critical one-moves后,需要更新Adjacent-Color Table。更新的原则:对于move(u,i,j),对于与u顶点相邻的顶点的行,第i列减一,第j列加一。如下:
5、为了更新Adjacent-Color Table,我们需要知道每一个顶点相邻的所有顶点,因此定义一个数据结构:
typedef struct Adjacent_Matrix{
int neighbor ; //number of current vertex
struct Adjacent_Matrix *next ; //point to the next vertex
}Adjacent ;
Adjacent * *A_Matrix ;
A_Matrix[i] 指向第i个Vertex对应的所有相邻节点,本文算法中,第一个neighbor其原本的功能可以用数组角标i代替,所以将其用于记录第i个Vertex相邻顶点的总个数。此时更新Adjacent-Color Table时只需遍历move(u,i,j)中u的所有相邻顶点即可。
以上说明都弄清楚了,则伪代码就一目了然了,伪代码如下:
3、Tabu Search
对于禁忌算法,我们还需要一个禁忌表,来记录被禁忌的属性和禁忌的长度。
如果某次迭代中执行了move(u,i,j),则顶点u将在接下来的tt次迭代中,禁止在回到颜色i。其中tt为禁忌长度。对于禁忌表TabuTenure[N][K],若记录禁忌长度,则每次迭代都需要更新,即对所有非零的元素进行减一,当我们记录的内容为:当前迭代次数+禁忌长度 的话,判断属性是否禁忌时,只需要比较当前迭代次数与禁忌表中值的大小,方法管理。
禁忌长度,可以采用常量的方式,也可以动态的改变。本文算法中,采用动态的改变禁忌长度,其值 = 2*f + rand()%10。其中f为目标函数的值,随着目标函数值的下降,禁忌长度逐渐减小。
禁忌算法需要判断每个邻居解的质量,无论是否属于禁忌解,对于禁忌解,判断是否为当前最好的解且优于历史最好解,若是,则进行解禁,否则只在非禁忌解中选择最好解,若有若干个同等优度的解,则随机选择一个。
其伪代码如下:
4、Hybrid Evolutionary
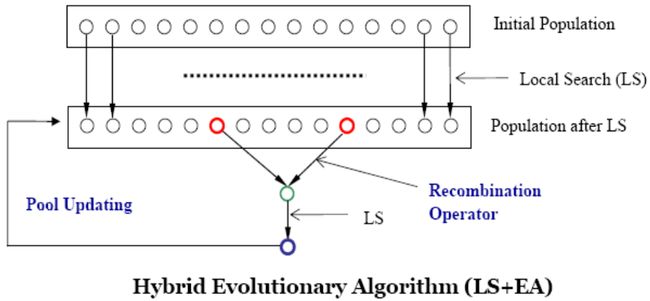
混合进化算法将局部搜索和进化算法相结合。进化算法是一个基于群体的算法(Population-based methods),混合进化算法可以将局部搜索的集中性和群体算法的疏散性相结合,达到更好的“集中性”和“疏散性”之间的平衡。
- 其主要思想是:维护一个比较小的“精英”群体,每个解都是经过局部搜索算法优化过的。对群体中的解采用进化算法的操作对其进行变换,并采用局部搜索算法对其优化。
- 当产生新解后,需要以解的优度和群体的多样性等指标为依据,来对群体进行更新。
- 与进化算法相比,混合进化算法中的群体更新策略更重要。
- 混合进化算法往往表现出比单纯的局部搜索或进化算法更优越的搜索性能。
伪代码如下:
- 初始化Population:可以随机选取若干个(一般是10~20),也可以通过启发式的方法,本文算法中使用终止条件较为宽松的禁忌算法。
- 选择双亲:随机的从Population总选择两个。
- 交叉操作:下文详细介绍
- 局部搜索:以上提到的局部搜索(LS),是泛指,可以是simple local search,tabu search,simulated annealing中的任意一种。
- 更新Population:替换掉Population选择质量最差的一个解。
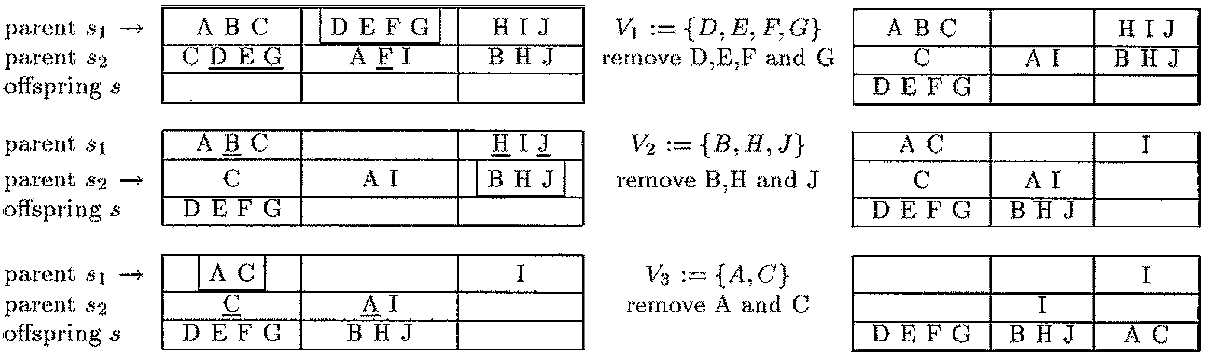
接下来着重讲解Recombination Operator,即交叉算子(Crossover)。对于图染色问题,考虑到质量优良的解,必有较多的独立集,因此继承双亲的最大独立集,来保证后代的优良性。具体操作以下图为例进行讲解:
1、相同格子中为着同一颜色的顶点,从S1中选择一个最大的集合{D,E,F,G},作为S的第一个颜色,然后将S1,S2中与S中相同的顶点删除(见图右上角)。
2、接下来,从另一个parent S2中选择一个最大的集合,此时S中集合有{C},{A,I},{B,H,J},显然选择{B,H,J},放入到S的第二个颜色中,同样将S1,S2中与S中相同的顶点删除(见图右侧中间)。
3、重复1、2步,直至S所有颜色被填入集合(见图右下角)。
4、对于剩余的,没有分配的集合,随机的选择一个颜色,即随机的将其放入S的任意格子中。同样进行删除操作。
5、重复4,直至所有顶点被加入到S。
伪代码如下:
参考资料:
- A memetic algorithm for graph coloring
- 华中科技大学吕志鹏老师:启发式优化课件