昨天随便找了个\(AGC\)肝一肝,结果发现自己啥都不会……再看了看当初的比赛结果人家全都是俩小时近乎\(AK\)的……
\(A-Poisonous\ Cookies\)
cout<\(B - Tree\ Burning\)
不难发现中间肯定有一个断点,满足它后面的全都是顺时针走过去的,它前面的全是逆时针走过去的。而且第一次走了之后,之后每一次都反向肯定最优。那么我们枚举一下断点,前缀和优化就好了
//minamoto
#include
#define R register
#define ll long long
#define fp(i,a,b) for(R int i=(a),I=(b)+1;iI;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
templateinline bool cmax(T&a,const T&b){return a'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
const int N=2e5+5;
int n,L,a[N];ll res,sum[N],suf[N];
int main(){
// freopen("testdata.in","r",stdin);
L=read(),n=read();
fp(i,1,n)a[i]=read(),sum[i]=sum[i-1]+(a[i]<<1);
fd(i,n,1)suf[i]=suf[i+1]+((L-a[i])<<1);
res=max(a[n],L-a[1]);
fp(i,1,n-1){
R int k=min(i,n-i);R ll tmp=sum[i]-sum[i-k]+suf[i+1]-suf[i+1+k];
cmax(res,tmp-min(a[i],L-a[i+1]));
i>k?cmax(res,tmp+(a[i-k]<<1)-a[i]):0;
n-i>k?cmax(res,tmp+((L-a[i+1+k])<<1)-(L-a[i+1])):0;
// printf("%d %lld\n",i,tmp);
}
printf("%lld\n",res);
return 0;
} \(C - Coloring\ Torus\)
首先有个构造方法,行列标号为\(0\)到\(n-1\)之后把所有\(i+j\)模\(n\)同余的格子标为同一种颜色(即每一条副对角线上填同一种颜色),易证显然合法
然而这样的话最多只能填\(500\)个,不够。我们考虑一条副对角线上填两种颜色,两种颜色交替,然而因为一条副对角线上的元素为\(n\)个,那么此时\(n\)必须为偶数才能合法。顺便注意可能不一定填满,也就是说需要某些副对角线上两种颜色,某些一种颜色,判一下就好了
//minamoto
#include
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;iI;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
R int res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
char sr[1<<21],z[20];int C=-1,Z=0;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
void print(R int x){
if(C>1<<20)Ot();if(x<0)sr[++C]='-',x=-x;
while(z[++Z]=x%10+48,x/=10);
while(sr[++C]=z[Z],--Z);sr[++C]=' ';
}
const int N=505;
int n,k,c,p,mp[N][N];
void solve(int p,int c){
for(R int i=0,j=(n+p-i)%n;i>1,n+=(n&1);
if(k==1)return puts("1\n1\n"),0;
p=0,c=1;
while(n-p \(D - Inversion\ Sum\)
我们枚举数对\(i,j(i
以\(a_x>a_y\)为例,那么我们需要\(q\)次转移之后\(x\)排在\(y\)的前面。我们设\(f_{t,i,j}\)表示\(t\)次转移之后\(a_x\)在\(i\)位置,\(a_y\)在\(j\)位置的方案数,初值为\(f_{0,x,y}=1\),其余全为\(f_{0,i,j}\)全为\(0\)。转移为(下面转移中这个\(x,y\)指的是第\(t\)次可以交换的两个数\(x,y\))
\[f_{t,i,j}=2f_{t-1,i,j}(i\neq x\ and\ j\neq y)\]
\[f_{t,x,j}=f_{t,y,j}=f_{t-1,x,j}+f_{t-1,y,j}\]
\[f_{t,i,x}=f_{t,i,y}=f_{t-1,i,x}+f_{t-1,i,y}\]
\[f_{t,x,y}=f_{t,y,x}=f_{t-1,x,y}+f_{t-1,y,x}\]
最终答案为\(\sum _{i
发现转移一层需要修改的状态是\(O(n)\)的,其它打个\(tag\)就行,所以转移的总复杂度就是\(O(n^2)\),算上枚举点对的话总复杂度是\(O(n^4)\)
让我们看看能不能快速对一个点对求出答案……一次\(dp\)的本质相当于是求出\((0,x,y)\)这个点到\((q,i,j)\)这个点的路径条数,那么我们可以倒过来,求出\((q,i,j)\)这个点到\((0,x,y)\)的路径条数,只要初始时将所有\(f_{q,i,j}(i
然后还要考虑\(i>j\)的情况,那么再递推一遍就行了
总复杂度为\(O(n^2)\)
//minamoto
#include
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;iI;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
R int res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
const int N=3005,P=1e9+7,inv2=500000004;
inline void Add(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int add(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))if(y&1)res=mul(res,x);
return res;
}
struct node{int x,y;}p[N];
int f[N][N],g[2][N],ans[2][N][N],a[N];
int n,q,res;
void solve(int pos){
int tag=1;
fd(t,q,1){
tag=mul(tag,2);
int x=p[t].x,y=p[t].y;
fp(i,1,n)g[0][i]=g[1][i]=0;
fp(i,1,n)g[0][i]=add(f[x][i],f[y][i]),g[1][i]=add(f[i][x],f[i][y]);
int c=f[x][y],d=f[y][x];
fp(i,1,n)f[x][i]=f[y][i]=mul(g[0][i],inv2),f[i][x]=f[i][y]=mul(g[1][i],inv2);
f[x][y]=f[y][x]=mul(add(c,d),inv2),f[x][x]=f[y][y]=0;
}
fp(i,1,n)fp(j,1,n)ans[pos][i][j]=mul(f[i][j],tag);
}
void init(){
fp(i,1,n)fp(j,1,n)f[i][j]=0;
fp(i,1,n)fp(j,i+1,n)f[i][j]=1;
solve(0);
fp(i,1,n)fp(j,1,n)f[i][j]=0;
fp(i,1,n)fp(j,1,i-1)f[i][j]=1;
solve(1);
}
int main(){
// freopen("testdata.in","r",stdin);
n=read(),q=read();
fp(i,1,n)a[i]=read();
fp(i,1,q)p[i].x=read(),p[i].y=read();
init();
fp(i,1,n)fp(j,i+1,n)Add(res,a[i]==a[j]?0:a[i]>a[j]?ans[0][i][j]:ans[1][i][j]);
printf("%d\n",res);
return 0;
}
\(E - Less\ than\ 3\)
不会了……太神仙了……
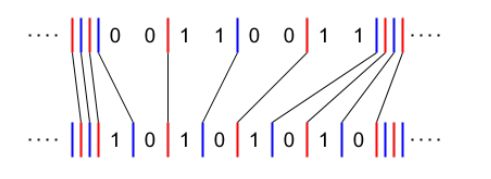
引用一下官方题解的图
上面的图的意思就是,我们在\(01\)之间连一条红线,在\(10\)之间连一条蓝线,那么一次操作如果不在边界上只会导致线的移动,如果是在边界上那么可能会导致多出一条线。而且易发现红线蓝线必定交替出现
我们先在左右两边无限红蓝红蓝延伸下去,那么我们的操作的目的就是使\(s,t\)的红线蓝线一一对应,一组对应边需要花费的次数恰好就是它们之间的距离
那么我们枚举一下\(s,t\)中那几条红线一一对应就行了
//minamoto
#include
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;iI;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
templateinline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
R int res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
int read(char *s){
R int len=0;R char ch;while(((ch=getc())>'9'||ch<'0'));
for(s[++len]=ch;(ch=getc())>='0'&&ch<='9';s[++len]=ch);
return s[len+1]='\0',len;
}
const int N=10005;
char s[N],t[N];int a[N],b[N],q[N],st[N],h,top,res;
int n,m;
void calc(){
top=0,h=0;
fp(i,1,n)st[++top]=0;
fp(i,1,n-1)!b[i]&&b[i+1]?st[++top]=i:0;
fp(i,1,n)st[++top]=n;
fp(i,1,n-1)!a[i]&&a[i+1]?q[++h]=i:0;
int mn=0x3f3f3f3f,now;
fp(i,1,top-n+1){
now=0;
fp(j,1,i-1)if(st[j])now+=st[j];
fp(j,0,h-1)now+=abs(q[j+1]-st[i+j]);
for(R int j=h;st[i+j]!=n;++j)now+=n-st[i+j];
cmin(mn,now);
}
res+=mn;
}
int main(){
// freopen("testdata.in","r",stdin);
n=read(),read(s),read(t);
fp(i,1,n)a[i]=s[i]-'0',b[i]=t[i]-'0';
if(n==1&&a[1]!=b[1])return puts("1"),0;
if(n==2&&a[1]!=b[1]&&a[1]==a[2]&&b[1]==b[2])return puts("2"),0;
calc();
fp(i,1,n)a[i]^=1,b[i]^=1;
calc();
printf("%d\n",res);
return 0;
}
\(F - Permutation\ and\ Minimum\)
还是不会……
如果有一对全都有数那么不影响答案不考虑,以及设全为\(-1\)的对数为\(cnt\),最终方案里这些可以任意互换所以答案要乘上\(cnt!\)
正着推啥也推不出来那么我们倒着推,设\(f_{i,j,k}\)表示已经填了所有小于等于\(i\)的数,其中有\(j\)个在数列中的数未匹配,\(k\)个不在数列中的数未匹配,转移可以看代码,注意如果匹配一个出现过的数有\(j\)种匹配方法
//minamoto
#include
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;iI;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
R int res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
int read(char *s){
R int len=0;R char ch;while(((ch=getc())>'9'||ch<'0'));
for(s[++len]=ch;(ch=getc())>='0'&&ch<='9';s[++len]=ch);
return s[len+1]='\0',len;
}
const int N=1005,P=1e9+7;
inline void Add(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
bool vis[N],nt[N];int a[N],q[N],f[605][305][305];
int n,m,t,cnt,ans;
int main(){
// freopen("testdata.in","r",stdin);
n=read();
fp(i,1,n<<1){
a[i]=read(),a[i]!=-1?vis[a[i]]=1:0;
if(i&1^1){
a[i]==-1&&a[i-1]==-1?++cnt:0;
a[i]!=-1&&a[i-1]!=-1?nt[a[i]]=nt[a[i-1]]=1:0;
}
}
fp(i,1,n<<1)!nt[i]?(vis[i]?q[++t]=1:q[++t]=0):0;
n=t;
f[n][0][0]=1;
fd(i,n,1){
fp(j,0,n>>1)fp(k,0,n>>1)if(f[i][j][k]){
R int v=f[i][j][k];
if(q[i]){
Add(f[i-1][j+1][k],v);
k?(Add(f[i-1][j][k-1],v),0):0;
}else{
Add(f[i-1][j][k+1],v);
k?(Add(f[i-1][j][k-1],v),0):0;
j?(Add(f[i-1][j-1][k],mul(v,j)),0):0;
}
}
}
ans=f[0][0][0];
fp(i,2,cnt)ans=mul(ans,i);
printf("%d\n",ans);
return 0;
}