线段树

定义

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。 [1]
对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

基本结构

线段树是建立在线段的基础上，每个结点都代表了一条线段[a,b]。长度为1的线段称为元线段。非元线段都有两个子结点，左结点代表的线段为[a,(a + b) / 2]，右结点代表的线段为[((a + b) / 2）+1,b]。
下图就是两棵长度范围为[1,5][1,10]的线段树。
长度范围为[1,L] 的一棵线段树的深度为log (L) + 1。这个显然，而且存储一棵线段树的空间复杂度为O(L）。
线段树支持最基本的操作为插入和删除一条线段。下面以插入为例，详细叙述，删除类似。
将一条线段[a,b] 插入到代表线段[l,r]的结点p中，如果p不是元线段，那么令mid=（l+r）/2。如果bmid，那么将线段[a,b] 也插入到p的右儿子结点中。
插入（删除）操作的时间复杂度为O（logn）。

实际应用

上面的都是些基本的线段树结构，但只有这些并不能做什么，就好比一个程序有输入没输出，根本没有任何用处。
最简单的应用就是记录线段是否被覆盖，随时查询当前被覆盖线段的总长度。那么此时可以在结点结构中加入一个变量int count；代表当前结点代表的子树中被覆盖的线段长度和。这样就要在插入（删除）当中维护这个count值，于是当前的覆盖总值就是根节点的count值了。
另外也可以将count换成bool cover；支持查找一个结点或线段是否被覆盖。
实际上，通过在结点上记录不同的数据，线段树还可以完成很多不同的任务。例如，如果每次插入操作是在一条线段上每个位置均加k，而查询操作是计算一条线段上的总和，那么在结点上需要记录的值为sum。
这里会遇到一个问题：为了使所有sum值都保持正确，每一次插入操作可能要更新O(N）个sum值，从而使时间复杂度退化为O(N）。
解决方案是Lazy思想：对整个结点进行的操作，先在结点上做标记，而并非真正执行，直到根据查询操作的需要分成两部分。
根据Lazy思想，我们可以在不代表原线段的结点上增加一个值toadd，即为对这个结点，留待以后执行的插入操作k值的总和。对整个结点插入时，只更新sum和toadd值而不向下进行，这样时间复杂度可证明为O(logN）。
对一个toadd值为0的结点整个进行查询时，直接返回存储在其中的sum值；而若对toadd不为0的一部分进行查询，则要更新其左右子结点的sum值，然后把toadd值传递下去，再对这个查询本身，左右子结点分别递归下去。时间复杂度也是O(nlogN）。

什么是区间加法

一个问题满足区间加法，仅当对于区间[L,R]的问题的答案可以由[L,M]和[M+1,R]的答案合并得到。
经典的区间加法问题有：

区间求和（∑Ri=Lai=∑Mi=Lai+∑Ri=M+1ai (L≤M<R)

∑i=LR​ai​=∑i=LM​ai​+∑i=M+1R​ai​ (L≤M 区间最大值（maxi=Lai=max(maxi=Lai,maxi=M+1ai) (L≤M

maxi=LR​ai​=max(maxi=LM​ai​,maxi=M+1R​ai​) (L≤M

不满足区间加法的问题有：

1.区间的众数
2.区间的最长不下降子序列

线段树的原理及实现

注意：如果我没有特别申明的话，这里的询问全部都是区间求和
线段树主要是把一段大区间平均地划分成两段小区间进行维护，再用小区间的值来更新大区间。这样既能保证正确性，又能使时间保持在log级别（因为这棵线段树是平衡的）。也就是说，一个[L…R]的区间会被划分成[L…(L+R)/2]和[(L+R)/2+1…R]这两个小区间进行维护，直到L=R。
下图就是一棵[1…10]的线段树的分解过程（相同颜色的节点在同一层）
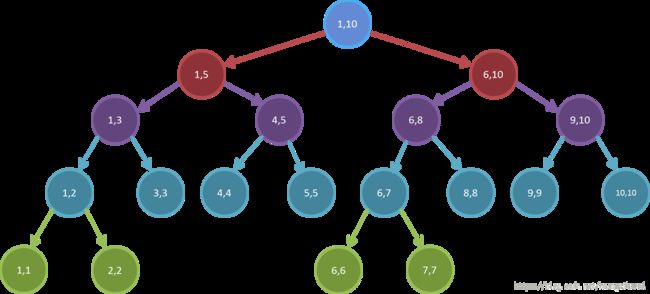可以发现，这棵线段树的最大深度不超过[log2(n−1)]+2[log2​(n−1)]+2（其中[x][x]表示对x进行下取整）
由于作者太菜，不会非递归的线段树，所以这里写的都是效率较低、较为常见的递归线段树。

储存方式

通常用的都是堆式储存法，即编号为k的节点的左儿子编号为k∗2k∗2，右儿子编号为k∗2+1k∗2+1，父节点编号为k div 2k div 2，用位运算优化一下，以上的节点编号就变成了k<<1,k<<1∣1,k>>1k<<1,k<<1∣1,k>>1。其它储存方式请见指针储存和动态开点。
通常，每一个线段树上的节点储存的都是这几个变量：区间左边界，区间右边界，区间的答案（这里为区间元素之和）
下面是线段树的定义：
struct node
{
int l/区间左边界/,r/区间右边界/,sum/区间元素之和/,lazy/懒惰标记，下文会提到/;
node(){l=r=sum=lazy=0;}//给每一个元素赋初值
}a[N];//N为总节点数
inline void update(int k)//更新节点k的sum
{
a[k].sum=a[k2].sum+a[k2+1].sum;
//很显然，一段区间的元素和等于它的子区间的元素和
}

初始化

常见的做法是遍历整棵线段树，给每一个节点赋值，注意要递归到线段树的叶节点才结束。
void build(int k/当前节点的编号/,int l/当前区间的左边界/,int r/当前区间的右边界/)
{
a[k].l=l,a[k].r=r;
if(l==r)//递归到叶节点
{
a[k].sum=number[l];//其中number数组为给定的初值
return;
}
int mid=(l+r)/2;//计算左右子节点的边界
build(k2,l,mid);//递归到左儿子
build(k2+1,mid+1,r);//递归到右儿子
update(k);//记得要用左右子区间的值更新该区间的值
}

单点修改

当我们要把下标为k的数字修改（加减乘除、赋值运算等）时，可以直接在根节点往下DFS。如果当前节点的左儿子包含下标为k的数（即对于左儿子区间[Llson…Rlson][Llson​…Rlson​]，Llson≤k≤Rrson

Llson​≤k≤Rrson​），那么就走到左儿子，否则走到右儿子（右儿子一定包含下标为k的数，因为根节点一定包含这个数，而从根节点往下走，能到达的点也一定包含这个数），直到L=R。这时就走到了只包含k的那个节点，只需要把这个点修改即可（这个点就相当于线段树中唯一只储存着k的信息的节点）。最后记得在回溯的时候把沿途经过的所有的点的值全部修改一下。

void change(int k/当前节点的编号/,int x/要修改节点的编号/,int y/要把编号为x的数字修改成y/)
{
if(a[k].l==a[k].r){a[k].sum=y;return;}
//如果当前区间只包含一个元素，那么该元素一定就是我们要修改的。
//由于该区间的sum一定等于编号为x的数字，所以直接修改sum就可以了。
int mid=(a[k].l+a[k].r)/2;//计算下一层子区间的左右边界
if(x<=mid) change(k2,x,y);//递归到左儿子
else change(k2+1,x,y);//递归到右儿子
update(k);//记得更新点k的值，感谢qq_36228735提出此错误
}

区间修改

其实如果会了单点修改的话，区间修改就不会太难理解了。
区间修改大体可以分为两步：

找到区间中全部都是要修改的点的线段树中的区间
修改这一段区间的所有点

先来解决第一步：
我们先从根节点出发（根节点一定包含所有的点，包括被修改区间），一直往下走，直到当前区间中的元素全部都是被修改元素。
当左区间包含整个被修改区间时，我们就递归到左区间；
当右区间包含整个被修改区间时，我们就递归到右区间；
否则，情况一定就如下图所示：

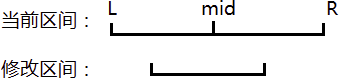
怎么办？这种情况似乎有些难了。
不过，通过思考，我们可以发现，被修改区间中的元素间，两两之间都不会产生影响。
所以，我们可以把被修改区间分解成两段，使得其中的一段完全在左区间，另一端完全在右区间。
很明显，直接在mid的位置将该区间切开是最好的。如下图所示：

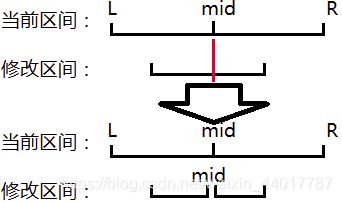
通过一系列的玄学操作，我们成功地把修改区间分解成一段一段的。但问题来了：我们怎样修改这些区间呢？
最暴力的做法是每一次都像建树一样，遍历区间内的所有节点，一一修改。但是这样的时间复杂度显然O(n2log2n)
O(n2log2​n)，比暴力O(n2)
O(n2)还多了个log，我要这线段树有何用？
这里就要引入一样新的神奇的东西——懒惰标记！

懒惰标记

标记的含义：本区间已经被更新过了，但是子区间却没有被更新过，被更新的信息是什么（区间求和只用记录有没有被访问过，而区间加减乘除等多种操作的问题则要记录进行的是哪一种操作）
这里再引入两个很重要的东西：相对标记和绝对标记。
相对标记和绝对标记

相对标记指的是可以共存的标记，且打标记的顺序与答案无关，即标记可以叠加。 比如说给一段区间中的所有数字都+a，我们就可以把标记叠加一下，比如上一次打了一个+1的标记，这一次要给这一段区间+2，那么就把+1的标记变成+3。
绝对标记是指不可以共存的标记，每一次都要先把标记下传，再给当前节点打上新的标记。这些标记不能改变次序，否则会出错。 比如说给一段区间的数字重新赋值，或是给一段区间进行多种操作。

有了懒惰标记这种神奇的东西，我们区间修改时就可以偷一下懒，先修改当前节点，然后直接把信息挂在节点上就可以了！
如下面这棵线段树，当我们要修改区间[1…4]，将元素赋值为1时，我们可以先找到所有的整个区间都要被修改的节点，显然是储存区间[1…3]和[4…4]的这两个节点。我们就可以先把[1…3]的sum改为3（(3−1+1)∗1=3
(3−1+1)∗1=3）,把[4…4]的sum改为1（(1−1+1)∗1=1
(1−1+1)∗1=1）然后给它们打上值为1的懒惰标记，然后就可以了。

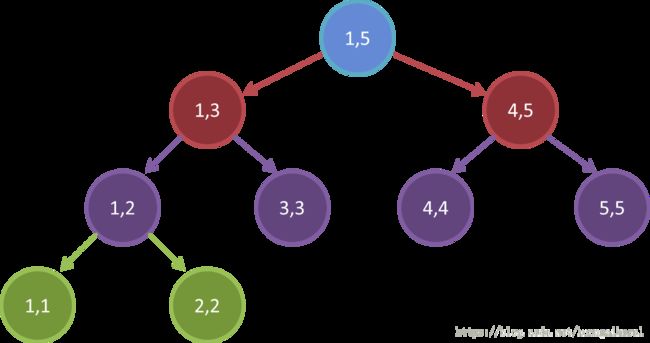
这样一来，我们每一次修改区间时只要找到目标区间就可以了，不用再向下递归到叶节点。
下面是区间+x的代码：
void changeSegment(int k,int l,int r,int x)
//当前到了编号为k的节点，要把[l…r]区间中的所有元素的值+x
{
if(a[k].ll&&a[k].rr)//如果找到了全部元素都要被修改的区间
{
a[k].sum+=(r-l+1)x;
//更新该区间的sum
a[k].lazy+=x;return;
//懒惰标记叠加
}
int mid=(a[k].l+a[k].r)/2;
if(r<=mid) changeSegment(k2,l,r,x);
//如果被修改区间完全在左区间
else if(l>mid) changeSegment(k2+1,l,r,x);
//如果被修改区间完全在右区间
else changeSegment(k2,l,mid,x),changeSegment(k*2+1,mid+1,r,x);
//如果都不在，就要把修改区间分解成两块，分别往左右区间递归
update(k);
//记得更新点k的值
}
请注意：某些题目的懒惰标记属于绝对标记（如维护区间平方和），一定要先下传标记，再向下递归。

下传标记

碰到相对标记这种容易欺负的小朋友，我们只用打一下懒惰标记就可以了。
但是，遇到绝对标记，或是下文提到的区间查询，简单地打上懒惰标记就明显GG了。毕竟，懒惰标记只是简单地在节点挂上一个信息而已，遇到复杂的情况可是不行的啊！
于是，懒惰标记的下传操作就诞生了。
顾名思义，下传标记就是把一个节点的懒惰标记传给它的左右儿子，再把该节点的懒惰标记删去。
我们先来回顾一下标记的含义：

标记的含义：本区间已经被更新过了，但是子区间却没有被更新过，被更新的信息是什么

显然，父区间是包含子区间的，也就是对于父区间的标记和子区间是有联系的。在大多数情况下，父区间和子区间的标记是相同的。因此，我们可以由父区间的标记推算出子区间应当是什么标记。
注意：以下所说的问题都是指区间赋值，除非有什么特别的申明。
如果要给一个节点中的所有元素重新赋值为x，那么它的儿子也必定要被赋值成x。所以，我们直接在子节点处修改sum值，再把子节点的标记改变一下就可以了（由于区间赋值要用绝对标记，因此当子节点已经有标记时，要先下传子节点的标记，再下穿该节点的标记。但是区间赋值会覆盖掉子节点的值，因此在这个问题中，直接修改标记就可以了）
代码如下：
void pushdown(int k)//将点k的懒惰标记下传
{
if(a[k].l= =a[k].r){a[k].lazy=0;return;}
//如果节点k已经是叶节点了，没有子节点，那么标记就不用下传，直接删除就可以了
a[k2].sum=(a[k2].r-a[k2].l+1)a[k].lazy;
a[k2+1].sum=(a[k2+1].r-a[k2+1].l+1)a[k].lazy;
//给k的子节点重新赋值
a[k2].lazy=a[k2+1].lazy=a[k].lazy;
//下传点k的标记
a[k].lazy=0;//记得清空点k的标记
}
那么区间赋值就很容易解决了。我们直接修改当前节点的sum，再打上标记就可以了。在大多数问题中，我们要先下传当前节点的标记，再打上标记。但由于这个问题的特殊性，我们就不用先下传标记了。

区间查询

上面我们很轻松地解决了修改的问题，于是我们就维护了一个完整的在线线段树了。但是光有维护是没用的，我们还要处理询问的问题。最常见的莫过于区间查询了，如询问区间[l…r]中所有数的和。
这其实和区间修改是类似的。我们也分类讨论：
当查找区间在当前区间的左子区间时，递归到左子区间；
当查找区间在当前区间的右子区间时，递归到右子区间；
否则，这个区间一定是跨越两个子区间的，我们就把它切成2块，分在两个子区间查询。最后把答案合起来处理就可以了（如查询区间和时就把两块区间的和加起来，查询最大值时就返回两块区间的最大值）
最后强调一个细节：记得在查询之前下传标记！！！
下面贴上查询区间和的代码：
int query(int k,int l,int r)
//当前到了编号为k的节点，查询[l…r]的和
{
if(a[k].lazy) pushdown(k);
//如果当前节点被打上了懒惰标记，那么就把这个标记下传，这一句其实也可以放在下一语句的后面
if(a[k].ll&&a[k].rr) return a[k].sum;
//如果当前区间就是询问区间，完全重合，那么显然可以直接返回
int mid=(a[k].l+a[k].r)/2;
if(r<=mid) return query(k2,l,r);
//如果询问区间包含在左子区间中
if(l>mid) return query(k2+1,l,r);
//如果询问区间包含在右子区间中
return query(k2,l,mid)+query(k2+1,mid+1,r);
//如果询问区间跨越两个子区间
}

指针储存和动态开点

上面我们用的都是堆式储存法。这种方法能快速地找出当前节点的父节点、子节点，但节点数很多，而无用节点也较多时就没有用了。我们可以用指针储存和动态开点解决这个问题。当然，大佬们也可以用离散化解决问题。
这其实就是用指针额外记录当前节点的子节点（有时可能还要记录父节点），且要用到节点时才新建节点。这样能大大地节省空间。
下面是结构体的定义：
struct node
{
int l/区间左边界/,r/区间右边界/,sum/区间元素之和/,lazy/懒惰标记，下文会提到/;
node *lson/左儿子/,*rson/右儿子/;
//这两个指针初始值为NULL，当儿子指针为NULL时表明它没有值
node(){l=r=sum=lazy=0;lson=rson=NULL;}//给每一个元素赋初值
};
node *root=new node;//根节点
inline void setroot()//根节点初始化
{
root->l=1,root->r=n;
}
inline void update(node *k)//更新节点k的sum
{
k->sum=0;
if(k->lson) k.sum+=k->lson->sum;
if(k->rson) k.sum+=k->rson->sum;
//注意要判断左右子节点是否存在
}
单点修改：
void change(node *k/当前节点/,int x/要修改节点的编号/,int y/要把编号为x的数字修改成y/)
{
if(k->l==k->r){k->sum=y;return;}
//如果当前区间只包含一个元素，那么该元素一定就是我们要修改的。
//由于该区间的sum一定等于编号为x的数字，所以直接修改sum就可以了。
int mid=(k->l+k->r)/2;//计算下一层子区间的左右边界
if(x<=mid)
{
if(!k->lson)//如果左儿子不存在，就新建一个
{
k->lson=new node;
k->lson->l=k->l;
k->lson->r=mid;
}
change(k->lson,x,y);//递归到左儿子
}
else
{
if(!k->rson)//如果右儿子不存在，就新建一个
{
k->rson=new node;
k->rson->l=mid+1;
k->rson->r=k->r;
}
change(k->rson,x,y);//递归到右儿子
}
}
其他操作相应地改一下就可以了，这里留给读者自己思考。
P.S：
提示一下：询问操作并不用新建节点。
其实动态开点不一定要用指针，也可以先开一个节点数组，每次新建节点时给它分配一个下标。不过个人觉得用指针方便一些。
原文链接：https://blog.csdn.net/huangzihaoal/article/details/81813454