多叉树——B树和B+树

目录

 

1 介绍

2 B树

2.1 B树的定义

2.2 B树的查找

2.3 B树的插入

2.4 B树的删除

2.5 B树的应用

3 B+树

3.1 定义

3.2 B+树的插入

3.3 B+树的删除

---

1 介绍

树家族是为了实现方便快捷的查找而存在的。树的高度是命中查找的一个不可抗拒的时间下限。在一定的数据条件下，树的高度和宽度是相互制约的。对于二叉树来说，虽然易于实现，却没有实际的价值。因为二叉树的宽度固定，使树的高度无法减小，因此出现了多叉树。B树、B+树都属于多叉树。MySQL和Berkeley DB都是基于B树原理而建立数据库的。B树是一种可实现的平衡多路查找树。平衡m叉查找树是指每个关键字的左侧子树与右侧子树的高度差的绝对值不超过1的查找树。

2 B树

2.1 B树的定义

B树在维基百科是这么定义的：“在计算机科学中，B树（B-Tree）是一种树状数据结构，它能够存储数据，对其进行排序并允许以O（log n）的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树，概括来说是一个节点可以拥有多于2个子节点的二叉排序树。与自平衡二叉查找树不同，B-树为系统最优化大块数据的读和写操作。普遍运用在数据库和文件系统。”

B树中所有节点的最大孩子节点数被称为B树的阶，通常用m来表示。一棵m阶B树可以是一棵空树，也可以是满足一下条件的m叉树。

1）每个节点最多有m个子结点，即每个节点最多有m-1个关键字；最少子节点要看是否为根节点，如果是非叶子节点的根节点，则至少要有2个节点，其他非根节点非叶节点至少要有[m/2]个节点，[m/2]表示m/2向上取整。

2）如果一个节点有n-1个关键字，则子节点有n个。这n-1个关键字按照递增的顺序排列。

3）每个节点的结构为：

n	k1	k2	....	kn
p0	p1	p2	...	pn

其中，n为节点中关键字的个数；ki为该节点的关键字且kipi为该节点的孩子节点指针且满足pi所指向的子节点的关键字都大于ki且小于k(i+1)，p0所指向的子节点的关键字小于k1，pn所指向的子节点的关键字大于kn。

4）节点内关键字互不相等且按照从小到大顺序排列。

5）叶子节点处于同一层；可以用空指针表示，是查找失败到达的位置。

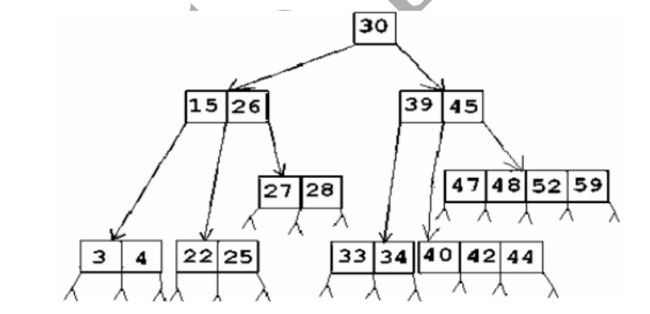
5阶B-树实例：

2.2 B树的查找

B树节点内的关键字是有序的，因此在节点内查找时除了顺序查找还可以使用折半查找。假设要查找的关键字为key。步骤如下：

1）先让key与根节点的关键字进行比较，如果key=k[i]，则查找成功；

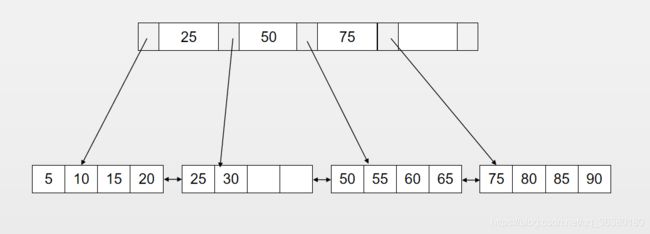
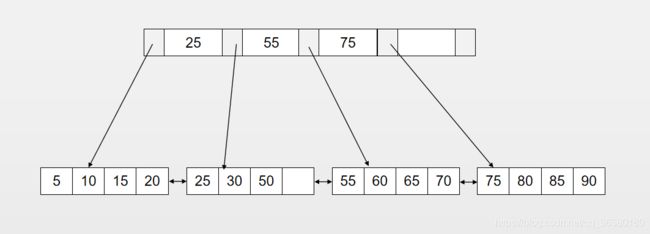
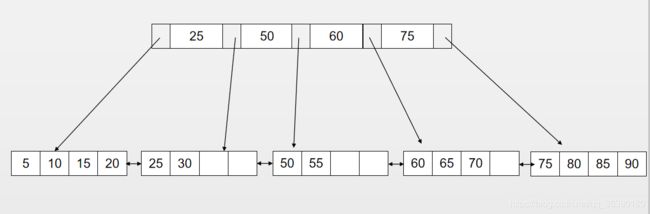
2）若key

3）若key>k[n]，则到p[1]所指向的子节点进行查找;

4）若k[i]

5）若遇到空指针，则查找失败。

2.3 B树的插入

在B树插入key时，需要判断key所在的节点的关键字的个数是否满足多叉树的条件。

2.4 B树的删除

2.5 B树的应用

为了将大型数据库文件存储在硬盘上，以减少访问硬盘次数为目的，在此提出了一种平衡多路查找树——B-树结构。由其性能分析可知它的检索效率是相当高的 为了提高 B-树性能’还有很多种B-树的变型，力图对B-树进行改进，比如B+树。

3 B+树

3.1 定义

由于B树的一个结点代表辅助的一个页或者块。一个节点到另一个节点的传送要求一次耗时的页交换，因此应该尽可能的减少节点访问。（如果要求B树中所有节点按升序打印，可以采用中序树遍历算法，这是很容易实现。）但对非叶子节点，每次只能显示一个键值，然后就得访问另一页。因此，应该改进B树，以更快的方式顺序访问数据，而不是使用中序遍历。B+树解决了这个问题。B+树的数据都存储在叶子节点中，分支节点均为索引，因此B+树用于数据库索引，B树适用于文件索引。
B+树和B树的差异在于：

1）有m个子结点的的节点的关键字有m个；

2）非叶节点仅具有索引的作用，跟记录有关的信息均记录在叶子结点中；

3）树的所有叶子结点构成一个有序链表，可以按照关键码排序的次序遍历全部记录。

相同点在于：

1）所有节点的子节点的个数最多为m；非叶根节点的子节点个数最少是2，非叶非根节点的子节点个数最少是[m/2]；

2）所有叶子节点都在同一层。

4阶B+树实例：

双向链表，每页可存放4条记录。

3.2 B+树的插入

Leaf Page Full	Index Page Full	操作
no	no	直接将记录插入到叶节点
yes	no	1、拆分叶节点（Leaf Page） 2、将中间节点放入索引节点（Index Page） 3、小于中间节点的记录放入左节点 4、大于等于中间节点的记录放入右边
yes	yes	1、拆分Leaf Page 2、小于中间节点的记录放入左边 3、大于等于中间节点的记录放入右边 4、拆分Index Page 5、小于中间节点的记录放入左边 6、大于等于中间节点的记录放入右边 6、将中间节点放入上一层Index Page

为了保持平衡，对于新插入的键值可能会做多次拆页操作（split），B+树主要用于磁盘，多次拆页意味着对磁盘多次操作，应该尽可能的减少对磁盘操作。因此B+树提供了旋转（rotation）操作。

旋转发生在Leaf Page满了但是左右兄弟节点还没满的情况下。通常情况下，左兄弟被首先检查用来做旋转操作。比如要插入70。

若按照拆页操作则是：

 

因此旋转使得少了一次拆页操作。

3.3 B+树的删除

B+树使用填充因子（fill factor）来控制树的删除，50%是删除因子可设的最小值，因为B+树属于多叉树，要满足多叉树最小分支数的条件。

Leaf Page Below Fill Factor	Index Page Below Fill Factor	操作
no	no	直接删除记录，若该记录还存在Index Page中，则更新Index Page
yes	no	合并叶节点及兄弟节点，并更新Index Page
yes	yes	1、合并叶节点及其兄弟节点 2、更新Index Page 3、合并Index Page及其兄弟节点 4、更新上一层Index Page