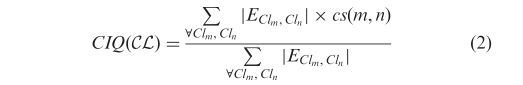BEMS：多个PPI网络全局多对多比对的骨干提取和合并策略

摘要：

动机：生物网络的全球多对多排列一直是比较生物网络研究的中心问题。给定一组生物相互作用网络，非正式目标是将相关节点分组在一起。对于蛋白质-蛋白质相互作用网络的情况，这样的基团有望形成功能上同源的蛋白质簇。为来自不同物种的网络构建这样的簇可能被证明在确定进化关系、预测具有未知功能的蛋白质的功能以及验证那些具有估计功能的蛋白质方面是有用的。

结果：构建同源蛋白质簇的一个中心非正式目标是保证每个簇由具有高度同源相似性的成员组成，通常通过序列相似性来确定，并且同一簇中涉及的蛋白质之间的相互作用在输入网络中是保守的。我们提供了多个蛋白质-蛋白质相互作用网络的全球多对多排列的正式定义，以达到这一非正式目标。我们证明了所提出的定义在计算上的难解性。针对该问题，我们提出了一种基于骨干提取和合并策略(BEMS)的启发式方法。最后，我们通过基于生物显著性测试的实验表明，所提出的BEMS算法比目前最先进的方法具有更好的性能。此外，BEAMS算法在执行速度和内存需求方面的计算负担比竞争算法更合理。

1、绪论

蛋白质及其相互作用几乎是所有生物过程的核心。在蛋白质-蛋白质相互作用(PPI)网络中，节点代表蛋白质，边对应于蛋白质对之间的相互作用。近年来，几种高通量技术与新的计算方法一起产生了许多生物的大规模PPI网络的提取(Aebersell和Mann，2003；Finley和Brent，1994；Goh和Cohen，2002；Marcotte等人，199；Skrabanek等人，2008年)。与这种巨大的数据增长相平行的是，已经提出了几个与此类网络的分析有关的问题公式，并开发了许多计算方法来进行比较研究。尤其是生物网络的比对问题一直是人们特别感兴趣的问题。这个问题背后的主要动机是从几个生物体的给定网络中检测功能上的同源蛋白。

文献中已经报道了两种类型的生物网络比对：局部网络比对和全球网络比对。前者旨在从输入网络中提取局部网络基序(子网络)；期望这些基序在序列和局部网络拓扑方面都具有合理的相似性(Flannick等人，2006年；Kalaev等人，2 0 0 9；K e l l e y等人，2004年)。另一方面，全球网络比对在全球范围内处理这一问题，目标是在所有网络和蛋白质中找到功能上的同源映射。一些提出的全局比对算法s u c h a s M i-G R A L(K u c h a i e v和Przˇulj，2011年)和SPINE(Aladag˘和Erten，2013年)仅对成对网络执行这些比对，而诸如等秩(Singh等人，2008年)和等秩N(廖等人，2009年)等其他算法在多个网络上执行比对。此外，全局比对算法还可以根据它们提供的映射类型而不同。一对一比对方法旨在产生比对，其中输出比对要么将网络中的一个蛋白质映射到其中一个网络中的恰好一个蛋白质，要么将该蛋白质保留在未映射的位置(Aladag˘和Erten，2013年；Chindelevitch等人，2010年；Singh等人，2008年)。已经提出了一对多的比对，用于包括代谢途径在内的其他生物网络的全球比对，其中一个途径中的每个代谢反应被映射到来自另一个途径的反应的子集(Abaka等人，2013年；Ay等人，2011年)。最后，对于多对多比对，目标是提取蛋白质簇，其中每个簇可能包括来自输入网络的任意数量的蛋白质(Flannick等人，2009；Liao等人，2009；Sahraeian和Yoon，2013)。作为比对的结果被定位到同一簇的蛋白质都有望组成一个功能上同源的基团。在全球网络对齐的所有三个版本中，多对多版本是最通用的。此外，就进化分子生物学的约束而言，它提供了一个更直观的定义；被研究生物之间的进化距离可能会有很大的差异，导致不同数量的蛋白质在不同的网络中功能相似。

本文的重点是来自不同物种的多个PPI网络的全球多对多比对。我们首先给出问题的形式组合定义。我们继续证明它的计算难解性，即使在受限的情况下也是如此。接下来，我们提供了问题的一般框架，将原始问题分解为两个子问题，即骨干提取问题和骨干合并问题。在f r m a l l y中，该框架中的每个骨架对应于一个密切相关的蛋白质中心基团，每个网络至多有一个。一旦确定了所有的骨架，后一个子问题涉及将共存几率更高的骨架合并到一组同源蛋白质中。我们为这两个子问题提供了启发式方法，这两个子问题共同构成了我们提出的基于骨干提取和合并策略的算法BEMS。我们对文献中提出的几种生物重要性度量进行了实验评估，并将其与全球最流行的多对多比对方法之一IsoRankN和最近提出的最先进的比对算法Smetana进行了比较。实验结果表明，与IsoRankN和Smetana相比，真实网络数据上的波束对齐提供了更一致的聚类。此外，考虑到问题的计算量很大，梁的异常运行时间和内存需求是所提供的框架和算法的进一步改进。

2、方法和算法

虽然在以前的工作中已经正式定义了该问题的一对一版本，但除了Graemlin 2.0(Flannick等人，2009年)基于参数学习的定义外，还没有针对交互网络对齐问题的全局多对多版本的正式组合定义，该定义实际上被定义为局部对齐的中间子问题。我们首先为该问题提供了一个正式定义的优化目标，该目标抓住了第一节中提供的非正式定义的本质。该定义基于Singh等人提供的全局一对一网络对齐问题定义的直观概括。(2008年)和阿拉达格˘和Erten(2013年)。

设G1？V1，E1？，G2？V2，E2？，…，Gk？Vk，Ek？为输入PPI网络，其中Gicori分别响应第i个PPI网络和Vi，Edenote分别响应Gi的节点集(蛋白质)和边集(相互作用)。L e t S表示边加权完全k部相似图，其中S的第i个划分是V，且S中的每条边(u，v)都被赋予一个正实权w(u，v)。该权重对应于u和v之间的序列相似性分数s(u，v)，通常假设s(u，v)是u和v的基本局部比特比特分数，其中u2Gi，v2Gj和i6？j，l e t S？是S的具有相同节点集的子图。什么？表示相似性图S的过滤版本，序列相似性相对较高的蛋白质对之间的边被保留。对于固定的S？，所有输入PPI网络的全局多对多对齐是寻找最大化以下分数的非重叠群集的最大集合CL？fCl1，Cl2，...，Clmg的问题：

在这里吗？是介于0和1之间的实数。它是一个平衡参数，用于确定网络拓扑相对于同源相似性在构建输出比对时的贡献权重。每个簇Client被定义为S？的一个完全c-部子图，w h e r e e 15c？K.如果不能向CL添加额外的簇，即在S？中没有更多的完整c部子图，则簇的集合CL是最大的。最大化AS分数并不能自动保证群集输出集的最大化。

方程中的CIQκCL表示团簇相互作用质量，是CL中所有团簇对之间相互作用守恒的量度。我们为每对群集CLm、CLn定义守恒分数，用cs(m，n)表示。L e t EClm，Cln表示具有不同簇CLm，CLn中的端点的所有PPI边的集合。如果Eclm，Cln？；，则得分cs(m，n)平凡为0。L e t sm，n表示由CLm，CLn中的节点共享的PPI网络的数目，并且设S0m，n是包含ECLm，CLn中的边的不同PPI网络的数目。我们指定cs≤m，n≤0if f s0m，n≤1a n？d cs≤m，n≤s0m，n=sm，反之亦然。前者的赋值反映了星团对之间没有相互作用守恒的事实。总体任务是两两网络对齐的边保持定义的推广。对于成对比对，边缘保护被分配一个二进制值，即一个网络中的PPI边缘在另一个网络中或者是保守的，或者不是。但是，对于多条路线，使用的定义可能会指定有理的保守值；参见图1。我们正式定义CIQ≠CL，如下所示：

在方程式(1)中，ICQ≠Cli？代表给定簇的内部簇质量，簇Cliand是所涉及蛋白质序列相似性的量度。设wmax∈u？表示入射到u上的任何边在S？中的最大权重。表示入射到客户端中的节点上的S边。ICQ§Cli？定义如下：

2.2 BEAMS算法

我们首先证明了对于固定的S？，全局多对多网络对齐问题在计算上是困难的。出于篇幅的考虑，我们把证明留给补充文件。

2.1号命题。对于全部？6/0，全局多对多对齐问题是NP-难的，即使对于两个PPI网络对齐并且S？中的所有边权重相等的受限情况也是如此。

考虑到这一NP难的结果，有必要设计有效的启发式算法来解决该问题。波束算法的一般方法可以在种子和扩展框架内描述。之前的几项网络对齐研究也基于相同的广泛框架(Kuchaiev和Przˇulj，2011年；Shih和Parthasarathy，2012年)。然而，如何正式定义种子、如何提取种子以及扩展的形式定义，这些共同构成了种子和扩展框架的主要组件，是我们方法的主要创新之处。关于方程(1)的簇定义，我们做了以下观察。每个簇Cli是一个完全的c-部图，可以细分为一组不相交的团，其中表示Cli的最大划分的大小。在a，c，t中，NIi是这样一个集合的最小可能大小，并且集合中的每个集团都有大小c0，其中1？C0？C.因此，我们认为原始的比对问题由两个子问题组成：骨干提取和骨干合并。主干定义为S？中的一个集团，一组合适的主干在一起形成一个簇。这样正式定义的每个主干可以被认为对应于一般种子和扩展框架内的种子。第一个子问题是从S？中提取不相交团的最小集合，wh_i_h_h完全覆盖S_i，并且当每个大小大于1的非平凡团在等式(1)的定义中被认为是簇时，这最大化了对齐分数。该集合是最小的，因为没有输出对的集团可以合并在一起以形成更大的集团。非正式地，每个骨架对应于一组最多具有来自每个输入网络的一个蛋白质的同源蛋白质集。因此，主干提取问题实际上可以看作多个网络的全局一对一对齐。如果一组骨干的并集提供有效的簇，即完整的c-部图，则称其为可合并的。我们将第二子问题定义为寻找可合并骨干群组的最小集合，使得没有更多的可合并群组剩余，并且当在等式(1)的定义中每个可合并骨干群组被认为是群集时，最大化所得到的AS分数。可合并组表示高度同源的蛋白质簇，因为来自不同网络的每对蛋白质通过过滤的相似图S？中的大权重边连接。因此，对集合施加不能进行进一步合并的约束意味着不应该有两个成对同源群集单独作为输出对齐的一部分的直觉。我们证明了即使是这些子问题在计算上也是困难的，并且我们为每个子问题提供了有效的启发式算法。在下文中，我们首先介绍S？构造的细节，然后对BEMS算法的两个主要步骤进行描述。

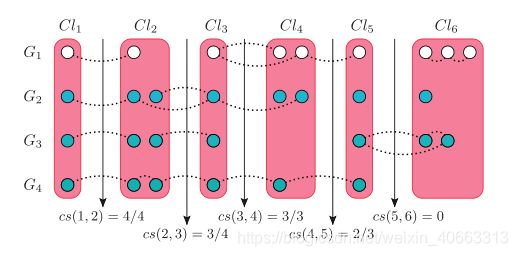
图1.覆盖所有重要案例的样本比对的保守分数。矩形组表示路线的簇。虚线边缘表示蛋白质与蛋白质之间的相互作用。每个PPI网络的蛋白质被绘制在单独的水平层上。此对齐的CIQ得分为iF4？4=4塔4？3=4塔4？3=3塔2？2=3塔0？=16.0：771。因为在任何其他聚类对之间不存在其他ppi边，所以只有所指示的cs分数对ciq有贡献。

2.2.1 S的构造

考虑到所考虑的网络的规模和多个网络构成研究对象的事实，有必要对完全序列相似图S进行适当的过滤，这主要有两个原因。首先，当S的大小增加时，即使是次优的多项式时间启发式算法也需要大量的计算能力。此外，就生物重要性度量而言，考虑完整的图S可能导致不正确的比对；来自不同网络的大多数蛋白质对在序列相似性方面不具有足够的重要性，并且使用与未过滤的相似性图S的比对可能比对几乎没有同源性的蛋白质。由于输入网络对之间的进化距离可能不同，我们使用了一种考虑网络对序列相似性相对差异的相对过滤方法。对于用户定义的阈值？，我们构造了过滤相似图S？，S？，s o t h a e a c h e d g e(u，v)是从S中去除的，如果w∈u，v？5？？分别表示来自u和v的网络中的任意u0、v0的最大值w∈u，v0？或w≠u0，v？的最大值，v？，w e r e max≠u，v？，w e r e max≠u，v？分别表示对于来自u和v的网络的任何u0，v0的最大值

2.2.2 主干提取

对于定义在BEAMS框架内的第一个子问题，我们证明了即使在受限的情况下，骨干提取问题也是NP-难的。完整的证明可以在补充文件中找到。

建议2.2。对于？6/0的所有值，即使在有两个输入网络且S？中的所有边权重相等的情况下，骨干提取问题也是NP-难的。

由于骨干提取问题是NP-hard问题，我们设计了一种迭代贪婪启发式算法，在考虑的网络数目为常数的情况下，该算法在多项式时间内运行。伪码如算法1所示。我们的算法使用了与最大边权重团(MEWC)相关的概念、基于邻域图构造的候选生成以及旨在优化AS得分的贪婪选择启发式。在MEWC问题中，假设输入图是边加权的，权值为非负实值，目标是找到边权和最大的团。

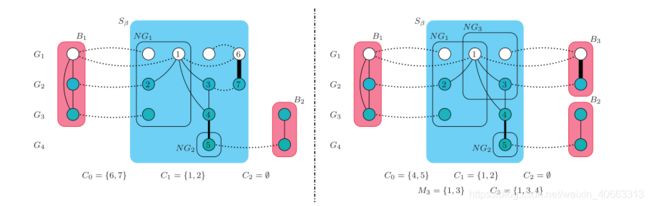
我们从一个空的骨干集和一个只由C0组成的候选集开始，这是S？的MEWC。算法主循环的第j次迭代包括四个主要步骤：从已有的j个候选中选择一个新的主干Bj，从S中删除该主干，生成新的候选Cj，最后更新所有现有的候选。图2描述了第三次迭代的示例实例上的每个主要步骤。第一步只是选择新的主干作为候选，当与所有现有主干一起考虑时，提供最高的得分。在第一次迭代中，很容易地选择C0作为第一主干B1。相对于除特殊候选C0之外的已有主干Bj定义的每个候选CJI，在迭代过程中随着S？更新而更新。为了通过函数调用生成一个新的候选Cj，我们首先构造了Bj的邻域图，它是Bj中所有节点的PPI邻域集合在S中的导出子图。如果邻域图不包含任何S边，则候选CJI为空。另外，我们找出该邻域图的MEWC，Mj，并通过构造Mjin S？的G-MEWC来生成Cj。这里，G-MEWC对应于广义MEWC，广义MEWC被定义为S中包含Mj的所有节点所需的最大边权重团。利用邻域图带来的相互作用守恒优势，构造邻域图的MEWC保证了由S边表示的同源序列相似性具有高度相似的主干候选者。另一方面，G-MEWC构建是一种预防措施，以使候选能够向其各自主干之外的网络进行可能的扩展。作为迭代中的最后一步，如果每个候选与新的主干Bj共享任何节点，则我们再次相对于其相应的主干和更新的S？重新生成每个候选。迭代继续进行，直到S？只包含孤立的节点，即那些零度的节点。

2.2.3 计算广义MEWC

我们使用深度优先的分枝定界型算法来找出包含给定节点集Mj所需的S？的广义最大边权重团。这里提供的描述假定您基本熟悉一般的分支定界框架；有关此框架的更多详细信息，请参阅Korf(2010)。分配Mj？；后，问题就归结为寻找MEWC的问题。与通常的分枝定界型算法一样，我们以深度优先的方式遍历搜索树T。T的第i级上的每个节点表示S？中大小为i？jMjj的团，该团必须包括Mj中的节点。在遍历期间，对于T的每个被遍历的节点u1，...，ui？jMjg，表示包含节点u1，...，ui？jmjj的集团，我们存储？的邻域集合，用N表示，其包含在节点u1，...，ui？jjj的公共邻域中的节点。你想要什么时候去看一看这张照片呢？(这句话的意思是：“你想要什么？”)。用EW Ian？？表示。L e t表示在集合N？中有一个结点的S？(PPI网络的集合)的分割号集合。在整个遍历过程中，我们存储搜索的最佳节点，表示为BEST？它的重量是最好的吗？？为了完成算法的描述，我们只需要指定分支规则和搜索的界限公式。一个节点的潜在权重的上限？在T中被分配给EW单塔P8ut2？P8r2代表N？？wmax？ut，r？pwmax？ut，w？e e wmax？ut，r？表示utt与S？的第r个划分中任意结点之间的最大权边的权重，n d pwmax？？表示一个可能的团Inn？的最大势权.f或r m a l l y，pwmax-N？？定义为jRep？n？n？j？的边权之和，f或r？m a l l y，pwmax？N？？定义为j代表n？j的边权之和，其中n d pwmax n？表示一个可能的团Inn的最大势权，f或r m a l y，pwmax n？定义为j表示n的边权之和。如果定义的节点的潜在权重？大于新的最佳节点？，则w eb r a n c h t node？，这意味着在下一级i ta1创建一个新的节点？0，其中？0ºfu1，...，UI塔jMjj，UI塔jMjj 1g，使得UI塔jMjj塔12 N？

图2.在算法1的主重复循环第三次迭代之前(左)和之后(右)，样本输入上的S？、主干和候选的状态。虚线边缘表示蛋白质相互作用。每个网络都绘制在单独的水平图层上。不同层之间的边代表S？边。左图：假设C0的AS得分在与现有骨干B1、B2考虑时大于C1的相应得分，则候选C0成为新生成的骨干B3。右：B3从S中删除？为了生成新的候选C3，首先构造B3的邻域图NG3。计算了NG3的MEWCm3，并将M3in S？的G-MEWC值作为新的候选C3。最后重新生成候选C0，该候选C0是与B3共享节点的唯一候选。假设S？的MEWC为边(4，5)，则其成为更新后的候选C0

2.2.4 主干合并

关于BEAMS算法的第二个主要步骤，我们首先提出了关于相应问题的计算复杂度的如下命题。完整的证明可以在补充文件中找到。

建议2.3。对于？6/0的所有值，即使在有两个输入网络且S？中的所有边权都相等的情况下，骨干合并问题也是NP-难的。

我们为骨干合并步骤提供了一种迭代的贪婪启发式算法。设MB表示可合并骨干群组的集合。最初，MB包含由第一个主干提取步骤提供的所有主干。它在算法的每一次迭代中通过贪婪选择策略进行更新，该策略类似于骨干提取步骤，使用候选生成和选择的思想。在每次迭代中，我们构造MB中的所有可合并组对，它们一起提供该迭代的所有候选集合。对于每个候选者，我们将候选者对视为单个组来计算MB的AS分数。以MB为单位的某些组可能由单个节点组成。这样的组被排除在AS分数计算之外。然后，我们选择提供最高分数的候选者，并通过合并该对来更新MB。当没有剩余提供最小集合MB的可合并对时，算法停止。最后，我们删除具有单个节点的组，并提供结果集作为群集的输出集。有关此步骤和整个算法的几个实现细节的完整讨论将留在补充文档中。

3、结果讨论

我们使用LEDA库在碳塔中实现了BEAM算法(Mehlhorn和Naher，1999)。完整的源代码、评估工具、所有数据和输出结果均作为补充材料的一部分提供。我们比较波束的两个算法是IsoRankN和Smetana。IsoRankN是全球多对多网络对齐文献中最流行的算法之一。研究表明，与其他流行的比对算法，如Graemlin 2.0、NetworkBLAST-M和MI-Graal相比，它在适合网络比对质量确定的措施下提供了更好的性能(Liao等人，2009；Sahraeian和Yoon，2012)。此外，IsoRankN和BEAMS算法的非正式优化目标在某种意义上是相似的，它们的目标都是最大化适当的优化评分函数，该函数通过适当分配的常数来平衡聚类蛋白质的同源相似性的贡献和簇对之间的边缘保守。因此，IsoRankN是我们广泛比较BEAMS算法的算法之一。我们在实验评估中使用的第二种比对算法是Smetana(Sahraeian和Yoon，2013)，这是最近提出的一种用于多个网络的概率多对多比对的方法。给出了不同？值下BEAM和IsoRankN的实验结果。以0.1为增量从0.3变化到0.7。BEMS算法还有一个额外的用户定义参数，即滤波率，设置为0.4。关于Smetana使用的参数设置，我们设置了Nmax？10、？*？0.9和？*？0.8。这些是原始文章(Sahraeian and Yoon，2013)中使用的设置。注意？*a n d？*不对应于？然后呢？在此定义的。

我们在真实和合成的PPI网络上进行了实验。关于前者，我们讨论了五个被广泛研究的物种的PPI网络的全球多对多比对结果：秀丽线虫(蠕虫)、黑腹果蝇(苍蝇)、智人(人)、小鼠(小鼠)和酿酒酵母(酵母)。BEMS算法需要PPI网络和比对蛋白质的成对序列相似性得分作为输入数据。所有这些数据都是从IsoBase(Park等人，2011年)数据库中检索的，该数据库与IsoRank、IsoRankN、Spin和Smetana算法使用的数据库相同。这些PPI网络是通过组合来自各种数据库的网络数据形成的，这些数据库包括DIP(Salwinski等人，2004年)、BIOGRID(Breitkreutz等人，2008年)、HPRD(Keshava Prasad等人，2009年)、MINT(Ceol等人，2010年)和INTERNAL(Aranda等人，2010年)。线虫网络有19756个蛋白质和4884个相互作用，黑腹线虫网络有14098个蛋白质和25054个相互作用，智人网络有22369个蛋白质和55168个相互作用，肌肉线虫网络有24855个蛋白质和592个相互作用，酿酒酵母网络有6659个蛋白质和82932个相互作用，总共有87737个蛋白质和168 630个相互作用。成对序列相似性分数对应于从Ensembl检索到的蛋白质序列的BLAST比特值(Hubbard等人，2009年)。关于合成数据的实验结果，我们使用了从NAPAbench检索到的合成PPI网络，这是最近提出的合成构建的网络对齐基准(Sahraeian和Yoon，2012)。由于空间上的考虑，我们在补充文件中介绍了我们对这些合成网络的实验评估。

在本文的后面，我们对这三种算法产生的比对结果进行了详细的评估。在下一小节中，我们将从数量属性的角度分析输出对齐。在此讨论之后，我们接下来提供基于最终比对的生物学意义的评估。

3.1 输出聚类分析

表1提供了BEMS、IsoRankN和Smetana算法生成的路线的定量分析摘要。为了进行更详细的分析，除了所有集群提供的总覆盖值之外，我们还通过基于c(集群中表示的网络数量)细分输出集来提供单独的分析。前四个多行分别为c？2、3、4、5的实例提供这些结果。BEAMS和Smetana的总覆盖率接近，尽管Smetana的覆盖率略大。两种算法的比对产生的聚类的总覆盖率远远好于IsoRankN比对；每种算法比IsoRankN比对几乎多50%的蛋白质。考虑到声称的正交性，这意味着BEAMS和Smetana通过提出大多数蛋白质的正交性关系，遗漏了更少未解释的数据。这种差异背后的主要原因是缺乏只包含来自两个网络的蛋白质的IsoRankN簇。这种缺陷可能会导致不合理的结论，因为考虑到所考虑的物种的成对进化距离有很大的差异，自然会期望蛋白质只来自两个物种的直系同源群体。

多行中用交互作用表示的顶行提供了由输出对齐产生的保守交互作用(CI)的数量，中间行表示群集之间的交互总数，而底部行提供了它们的比率。如果PPI的CS分数大于零，即，相互作用发生在来自不同簇的一对蛋白质之间，该对蛋白质进一步包含来自另一PPI网络的至少一对相互作用的蛋白质，则假定该PPI是保守的。对于？的所有实例，BEMS算法比IsoRankN提供更多的CI。此外，这种优势不仅仅是因为光束对准产生了大量的集群；考虑到CI的数量与集群之间相互作用的总数量的比率，可以观察到光束对准在所有集群之间保持了更大的现有边缘的比率。就CI的数量而言，Smetana的性能优于BEAM。一个可能解释这一结果的原因是产生的簇的大小；Smetana排列的平均簇大小为4.36，而光束排列的平均簇大小为3.90。具有较大群集大小的对齐在提供更多配置项数量方面有更好的机会。在极端情况下，简单地通过网络的最大割集将输入网络细分为两个簇可以提供很大的相互作用守恒性，甚至导致100%的守恒率。另一方面，较大的群集大小可能会降低ICQ分数，该分数旨在测量内部群集质量，从而降低整体比对的质量。通过检查提供公式(1)中定义的路线的AS分数的表的最后一行，这一点变得很明显。对于的每个相应值？在AS定义中使用的梁路线比IsoRankN和Smetana路线都提供了更好的结果。我们注意到，对于Smetana，表中提供的AS分数是在？25 0.3设置下计算的。斯美塔纳的其余AS分数分别为0.42、0.36、0.30、0.24，而？值分别为0.4、0.5、0.6、0.7。此外，正如在Sahraeian和Yoon(2013)中指出的那样，简单地比较CI计数可能具有误导性，除非相互作用保守是在同源群体之间。下一小节提供了一个用COI(保守的正交相互作用)表示的度量，它将这一事实考虑在内。

注：对于表格的前五个多行，顶行对应于生成的簇的数量，而底行提供输出簇中的蛋白质总数。前四个多行分别提供了c？2、3、4、5实例的结果，其中c表示正在考虑的集群中的网络数量。在每行中，最高值以粗体显示。

3.2 基于生物学意义的评估

与以前的PPI网络比对研究类似，我们的生物学意义评估是基于分层基因本体(GO)分类，其中蛋白质用适当的GO类别注释，组织成有向无环图(Ashburner等人，2000年)。标准化蛋白质的GO注释，类似于Aladag˘和Erten(2013年)的评估方法，廖等人。(2009)和Singh等人。(2008)，我们将蛋白质标注限制在GO有向非循环图的第五层，方法是忽略较高层的标注，并在受限的层次上用它们的祖先替换更深层次的类别标注。蛋白质标注被用来衡量生成的聚类的一致性。如果一个簇的至少两个蛋白质被一些GO类别注释，则该簇被注释。

如果一个带注释的簇的所有蛋白质共享至少一个共同的标准GO注释，则该簇被认为是一致的。表2的前五个多行中提供了波束、IsoRankN和Smetana对齐的一致性评估。这些多行中的每个行的顶部行指示带注释的簇的数目，中间行提供一致簇的数目，最后底部行指示一致簇与带注释簇的比率。在以前的一些比对研究中，这个比率被称为特异性(Sahraeian and Yoon，2012)。考虑到完整的一组带注释的群集，很明显，就一致群集的数量而言，波束对齐比IsoRankN和Smetana的性能更好。此外，排列的束团比IsoRankN和Smetana产生的束团更具体。

为了测量所提供的比对结果的灵敏度，我们使用Flannick等人中的灵敏度定义。(2009)。类似于该定义，对于给定的GO类别，让其最接近的簇表示包含用该GO类别注释的最大数量的蛋白质的簇。然后，对齐的敏感度被定义为所有GO类别上的对齐节点的分数的平均值，这些节点用GO类别标注，这些节点也在其最接近的群集中。正确节点是反映比对敏感性的另一个指标(Sahraeian and Yoon，2012)，其定义为所有一致簇中注释蛋白质的总数。在相应的多行中，顶部提供此数字，而底部提供正确节点与路线中带注释的节点数量的比率。此外，我们还提供了一种替代度量来测量相对于替代对齐的正确对齐节点。BEAMS列下显示的RCNC1值提供了BEAMS对齐中一致簇中的注释蛋白质数和IsoRankN对齐中不一致簇中的注释蛋白质数。设置。IsoRankN列下的RCNC1值提供了完全相反的结果。类似地，RCNC2测量波束和Smetana对齐之间类似的相对正确的节点数。我们注意到，对于Smetana，表中提供的RCNC2分数是相对于±0.3设置的光束对齐。Smetana相对于设置为？？0.4、0.5、0.6、0.7的波束对齐的其余分数分别为5330、5332、5400和5367。与IsoRankN和Smetana相比，波束对准提供了更好的灵敏度、正确的节点数和相对正确的节点数。

平均归一化熵(MNE)是先前研究中使用的另一个一致性评估指标(Liao等人，2009；Sahraeian和Yoon，2012)。注记团簇Clx的归一化熵定义为NE≠CLX？1logd？Pd？1pi？Logpi，其中pi是带有注释Goi的Clx中蛋白质的分数，a n d d表示CLx中不同GO注释的数量。F或r MNE这些值的总和在带注释的簇的总数上求平均。较低的MNE值表示一致性较好。另一个一致性评估度量是ALADAG、˘和ERTEN(2013年)中定义的Go一致性(Go Consistency)。因为GOC是为一对网络的一对一比对而定义的，所以我们通过归一化分数将该定义扩展到多个网络的多对多比对。对于一个带注释的簇CLX，l e t GOINT§CLX？和Gouni§CLX？分别表示CLX中所有蛋白质的GO注释的Clxa和Th e u n i On Set t中的GO注释的交集。Th e n o r m a l i z e d GOC得分Ngoc被定义为所有注释聚类上jGOintj=jGOunij的加权平均值，其中每个聚类的权重是其包含的注释蛋白质的数量。就更好的一致性而言，更大的Ngoc值是可取的。W i t h r e s p e c t o b o h h m e t r i c s，m ne和ngoc，BEAMS算法的性能明显优于IsoRankN和Smetana。

最后，正如上一小节末尾指出的那样，CI分数本身可能不是一个适当的衡量标准。重要的是要检测所提供的交互保守是否是虚假的，或者确实与直系节点之间的真实CI相对应。与Sahraeian和Yoon(2013)类似，我们使用COI度量来实现这一目的。对于给定的对齐，它表示一致群集之间的CI数量。IsoRankN和Smetana的COI分数有点相似，而BEAMS提供了一个明显的大分数。与IsoRankN和Smetana相比，BEAMS提供了几乎1000个同源簇之间的CI。COI/CI比率可能为Smetana在上一小节中讨论的成功实现高CI得分提供了一个很好的线索。梁的这一比例为48%，而斯梅塔纳的这一比例低至20%。这表明，Smetana以牺牲非同源节点之间可能的虚假保守为代价，积极地保存相互作用。

除了这些旨在测量输出比对的生物学意义的评估指标外，我们还提供了一个特定的聚类实例，该实例由相同数据集上的波束、IsoRankN和Smetana的比对产生。由于篇幅所需，补充文件中提供了关于讨论这一对齐情况的详细情况。

3.3 运行时间要求

设V表示所有PPI网络中的节点集，？Max表示任意输入PPI网络中任意节点的最大度，最后设？表示S？中的最大次数。在合理的假设下，光束的运行时间是由O≤V_2~2？K~1？所限定的，在合理的假设条件下，光束的运行时间是由O≤V_2？K≤K的。算法的正式运行时间分析可以在补充文档中找到。与IsoRankN相比，BEAMS和Smetana的一个重要优势是其卓越的执行速度。对于本节的IsoBase数据实验，IsoRankN平均需要近40小时才能完成执行。BEAM和Smetana的时间要求相似。在相同的计算设置下，两者都需要近半个小时才能完成。

此外，BEAM的内存需求比Smetana要好得多；前者在IsoBase数据上的实验需要2.5 GB，而后者在相同的输入上几乎需要4.5 GB。所有所需CPU时间的详细信息可在补充文档中找到。

4、结论

给出了多PPI网络全局多对多比对的组合优化公式。我们证明了这个问题在计算上是难以解决的。在通用的种子和扩展框架的基础上，我们提出了一种新的启发式算法BEAMS。我们将BEAMS算法与两种流行的最新算法IsoRankN和Smetana进行了比较。使用IsoBase的网络数据，我们发现在文献中提出的几个生物学重要性度量方面，BEAMS算法优于这两种算法。我们注意到，除了网络对齐问题的多对多版本之外，之前也研究过包括一对一和一对多的版本。由于缺乏不同版本产生的对准评估的标准标准，因此将波束与针对一对一或一对多对准提出的算法进行比较超出了本文的范围。进一步的研究涉及到为各种比对问题版本设计评价标准，这将增强我们对比较生物网络分析的理解。