BioFabric Visualization of Network Alignments

摘要

动机：在过去的十年中，已经开发了数十种全球网络对齐算法，但由于缺乏有效的网络可视化工具，很难直观地了解这些不同算法的优缺点。

结果：我们为现有的网络可视化工具BioFabric创建了一个新的插件，称为VISNAB：使用BioFabric的网络对齐可视化。我们利用BioFabric独特的布局方法(节点是由代表边缘的垂直线连接的水平线)来帮助理解网络对齐、评分和性能。我们的可视化工具使用户能够清楚地发现通过标准拓扑测量无法检测到的路线中的缺陷，并为改进路线提供洞察力。我们介绍了评估比对质量的新方法和理解成对全球网络比对的新方法。

绪论

网络对齐是在两个网络的节点之间找到映射的过程，从而允许在映射的节点之间传输信息。在过去的十年中，蛋白质-蛋白质相互作用(PPI)网络的可用性不断提高，这刺激了网络比对算法的发展。特别是，PPI网络的比对揭示了蛋白质功能和相似性方面的关键见解(Kuchaiev等人，2010年)，这反过来又提供了对人类疾病机制(Uetz等人，2006年)和人类衰老过程(Milenkovi‘c等人，2013年)的更好理解；这可能使生物信息能够跨物种转移。

创建BioFabric网络可视化工具是为了帮助可视化和分析大型复杂网络(Longabaugh，2012)。传统的节点-链接图(图1)将节点描述为点，而BioFabric将节点表示为水平线。边表示为连接两条节点线的垂直线，并在链接线的两端绘制小方块。有一个∗应该发送给他(wjrl：可视化；wbh：对齐)。每行一条节点线，每列一条边线，排列在严格规则的网格上。使用此方法时，边不可能重叠，而且由于链接可以沿适当的节点线段在任何位置开始和终止，因此完全可以自由决定在何处绘制链接。这种边放置的灵活性可用于创建呈现有意义的边语义分组的网络可视化；参见图1。

BioFabric使用的方法与“可见性表示”有一些相似之处(Tamassia and Tollis，1986；Blakley，1987)，McAllister(1999)中出现了一个使用“节点作为线”的小示例。但是BioFabric没有约束节点被表示为离散的块，并且根本不试图最小化链路交叉。事实上，BioFabric已经证明，即使在节点和边线之间有数百万个交叉点，也可以创建有用的网络可视化。

以前已经有工具解决了可视化网络比对的问题(谢等人，2014年；Malek等人，2016年)。这些工具仍然依赖于节点链接图的变体，因此受到困扰这项技术的基本问题的困扰：对齐随着它们变得更大和更复杂而变得更难可视化。然而，BioFabric提供的优势允许一种全新的方法来可视化网络比对。我们通过创建一个新的BioFabric插件来利用这些特性，我们称之为VISNAB：使用BioFabric的网络对齐可视化。此插件可用于以显示拓扑测量和有关网络对齐算法性能的信息的方式可视化和分析网络对齐。

2 方法论

2.1 概述和命名

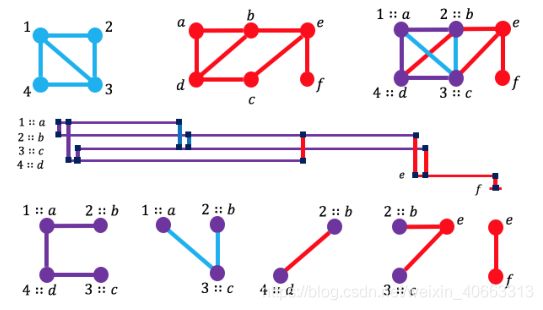
图1说明了BioFabric如何深入了解网络对齐的质量，并介绍了我们在本文中使用的基于颜色的命名法。图上方显示了三个网络的传统节点链路图：较小的蓝色网络(左上角)与较大的红色网络(中上角)一对一对齐，从而创建了一个组合网络(右上角)，该网络是两者的联合。当节点或边在此过程中匹配时，我们将其称为紫色。当较大网络中的某个节点不匹配时，我们将其称为红色。图的中间行显示了BioFabric如何表示组合的网络：节点用水平线表示，边用垂直线表示。对于本例，为了使比较更加具体，此图在两个方面与实际的BioFabric表示有所不同。首先，此处的节点绘制为紫色和红色，以便与节点链接图中的对应节点相匹配；其次，不同类别的边被明显分组。在BioFabric中，为了允许网络对齐的缩放，节点颜色以严格的模式循环，边在统一的规则网格上组织。

图1.与BioFabric的网络对齐。顶行使用传统的节点链接图来显示简单的对齐，其中较小的蓝色网络(左上角)与较大的红色网络(中上角)对齐。生成的对齐网络(右上角)将对齐的节点和边表示为紫色；对齐到上的节点1标记为1：：a。未对齐的元素保持蓝色或红色。中间一行显示了BioFabric如何可视化相同的右上角网络，其中节点绘制为水平线，边绘制为垂直线。下面一行说明了正文中描述的五个不同的链接组。(请注意，标准的BioFabric演示文稿在统一的规则网格上排列链接；此处显示的间隙有助于理解此示例。)。此图中未显示的是每个节点的节点组，这些节点组在本图中没有排序：1：：A：(P：B)；2：：B：(P：P/B/PRP/PRR)；3：：C：(P：P/B/PRR)；4：：D：(P：P/PRP)；E：(R：PRR/RRR)，f：(R：RRR)

2.2 节点和链路分组

图1展示了如何使用BioFabric来提供高度组织的网络对齐演示。特别是，请注意如何将对齐的紫色节点分别分组在顶部行中，而将未对齐的红色节点一起分组在底部。此外，紫色、蓝色和红色的边缘也分别分组。

如图1底部所示，在对齐的网络中实际上有五类不同的边。从左到右，我们有紫红色边缘、蓝色孤立边缘和三种不同类别的红色未接触边缘。这些红色边缘类是基于入射到边缘上的两个节点的颜色定义的：都是紫色、都是红色，或者都是一个。我们将这五个不同的类别称为网络对齐的链路组；表1中列举了它们，以及我们用来描述每个类别的符号(例如PRR)。

此外，根据入射到节点上的边的类型，可以将紫色和红色两大类节点进一步细分为节点组；这些类别及其符号在表2中列举。例如，非单个(组17-19)的红色节点可以被分类为具有节点边界，即：1)只有紫色(所有入射边都是PRR)，2)紫色和红色(入射边都是PRR和RRR)，或3)只有红色(所有入射边都是RRR)。

我们可以使用这些节点和链路分组集来创建网络对齐的有组织的可视化，其方式为对对齐的属性提供新的见解。

表1。BioFabric链接组的枚举。

表2.BioFabric节点组的枚举

2.3 网络合并

与提供例如两个对准的网络的并排比较相反，我们首先将两个网络合并为一个，然后使用我们的节点和链路组定义来表征该合并的网络的元素。我们使用以下方法将这两个网络合并为合并的网络。设G1=(V1，E1)和G2=(V2，E2)是|V1|≤|V2|的两个网络。从G1到G2的两两全局比对是一个内射函数a：V1→V2；V1中的每个节点都映射到V2中的不同节点。合并后的网络G12=(V12，E12)由两个网络中的节点和边组成。具有a(U)=v的所有对准节点u_∈_v1、v_∈_v2被组合成一个节点n并添加到v12。组合节点n以u：：v格式标记，V2中未对齐的节点也被添加到V12。E12由E1和E2中的所有边组成。对齐的边是边(U1，U2)∈E1：(a(U1)，a(U2))∈E2。对齐的边(链接组P)在E12中仅表示一次。因此，边总数|E12|因路线不同而不同。

2.4 新指标

当前使用的大多数仅限拓扑的网络对齐方法在广泛的生物测试集上执行得相当差，特别是当使用节点正确性(NC)来评估对齐时。当正确对齐已知时，Nc是节点u∈V1正确对齐的分数。事实上，NC值的细微差异，即使在统计上意义重大，对于评估纯粹的拓扑驱动的比对来说，也可以说没有太多的信息。我们在这里演示了评估对齐性能的其他方法可以为不同技术的行为提供更丰富的见解。

在定义了对齐网络中的节点和边集合上的节点组和链路组等价关系之后，我们可以使用它们来定义新的度量，该度量可以用于在两个网络之间存在黄金标准的已知“完美”对齐(NC=1)的情况下评估对齐的性能。我们可以通过比较给定对齐中的节点和边在分组中的分布与在完全对齐中找到的分布进行比较来做到这一点。为此，我们创建了节点组相似性(NGS)和链路组相似性(LGS)度量。NGS和LGS都是使用分别表示分布在20个节点组和5个链路组之间的节点和链路的比例的向量来计算的。例如，节点组NG1、NG2、...、NG20的NGS矢量r为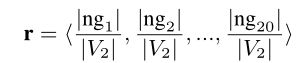

计算给定排列的矢量与已知完全排列的矢量之间的角相似度。对于仅包含正元素的向量，角度相似性=1−2θ/π，其中θ是对齐向量与完全对齐向量之间的角度。选择角度相似度(而不是余弦相似度)是因为它在小角度的情况下表现出从最佳值更快的衰减。

我们采用的另一个有用的度量是Jaccard相似性(JS)(Jaccard，1901)。设N(V1)={v2∈v2：(v1，v2)∈E2}是G2中节点v1的邻域。对于结点x，y，∈V2，设N0(X)是x的邻域，不考虑y，并设Ixy2是这两个结点之间可能边的修正测度。因此，如果y∈N(X)，则N0(X)=N(X)−y且Ixy=1，否则N0(X)=N(X)且Ixy=0。让N0(Y)类似地定义。我们两个节点之间的扩展JS定义σ：V2×V2→[0，1]定义为：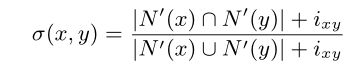

直观地说，如果两个对齐的节点共享一组相同的邻居(忽略它们之间可能的自链接)，则它们的得分为1.0，因此无法仅使用拓扑进行区分。给定对齐a和V1和→V2的完美对齐，我们对整个网络的JS度量定义为：

值得注意的是，如果两个节点在拓扑上相同(例如，两个节点是同一集团的成员)，则JaccardSimilarity不会惩罚未对齐。还要注意JS如何为节点具有几乎相同的邻居集的对齐提供“部分积分”。与节点正确性相比，当路线的生成仅依赖于拓扑时，这可以说是要使用的正确度量。当用户提供黄金标准的“完美”对齐文件作为设置步骤的可选部分时，VISNAB会在一个对话框中显示所有这些指标以及其他常用指标。

2.5 节点和链路组布局算法

一旦我们创建了一个合并的网络，我们的任务就是提供一个信息丰富的网络布局，将节点和边组织到我们设计的分组框架中。所有BioFabric网络布局都是通过创建节点的线性排序和边的线性排序来完全定义的。布局节点的默认技术很简单：它使用广度优先搜索从最高程度的节点开始创建节点的线性排序，其中按从最高程度到最低程度的顺序访问相邻节点。

这项基本技术使用单个队列进行广度优先搜索，可以对其进行修改，以创建使用我们定义的基于对齐的分组来组织节点的布局。具体地说，我们对其进行了调整，以便对20个节点组中的每一个使用单独的队列。生成的布局在很大程度上保留了与默认算法相同的总体结构，同时确保节点在每个节点组带中组织良好。在搜索期间访问节点时，会将它们添加到与其节点组对应的队列中，并按照表2中列出的顺序处理这些节点组队列。补充资料中提供了对该算法的更完整描述。

如果提供了完全对齐，则用户可以选择将正确对齐和不正确对齐的节点分别布置在不同的节点组中。用户可以选择基于传统NC测量或基于我们的JS测量的正确对齐标准。如果选择JS，则用户可以设置阈值β∈[0，1]，因此如果σ(v，ap(U))为≥β，则表示对齐的节点u：：v是正确的。

默认的边布局算法使用Longabaugh(2012)中描述的现有链接组特征的略微修改版本，可用于将边组织成五个链接组。新的修改允许在每个网络的基础上对标记有特定关系的边进行连续分组；以前，这只能在每个节点的基础上完成。使用这个新的修改，表示边缘的链路组(表1)的五个标签中的一个被分配给网络中的每个边缘。然后根据这些标签将边缘划分为五个链路组，如图1所示。

2.6 对齐周期布局

用于评估对齐算法的性能的常用方法是将网络的子集与其自身对齐，其中较大的网络包含相同数量的节点但包含更多数量的边(Collins等人，2007年；Kuchaiev等人，2010年；Malod-Dognin和PrˇZulj，2015年；Mamano和Hayes，2017年)。为了让研究人员更好地理解这些分析，我们开发了一种特殊的网络对齐布局方法，突出了对齐问题。该技术利用了这样一个事实，即如果网络与其自身对齐，则该对齐可以被视为覆盖节点集的一组循环，因为网络中的每个节点都保证与网络中的某个其他节点对齐。正确对齐的节点的循环长度将为1，A→A，但A→B和B→A的未对齐将创建长度为2的循环。更严重的未对齐会产生更长的路径，但每条路径都保证是一个循环。

由于BioFabric中的节点布局只是节点的线性排序，因此这些对齐周期为指定该排序提供了自然的基础；所产生的布局生动地描绘了对齐的本质。我们首先在第一行中放置一个节点，然后使用包含该节点的对齐循环来指定循环中所有其余节点的行顺序。如何对这些周期排序的决定再次源自对BioFabric的广度优先搜索默认布局算法的修改，该算法在Longabaugh(2012)中进行了描述。对于对齐周期布局，在处理下一个邻居之前，只需先放置邻居的周期中的所有节点。

虽然当网络与其自身对齐时该技术最容易描绘，但是该方法已被推广以处理从一个网络到具有更多节点的另一个网络的网络对齐。在这种情况下，对齐会创建一组路径而不是循环，因为并非大型网络中的所有节点都会映射到小型网络中的节点。对于路径，当在搜索中第一次遇到路径中的任何节点时，该算法将属于该路径的所有节点放置在该路径中。最后，如果两个网络中的节点位于不同的名称空间，则用户可以提供映射。

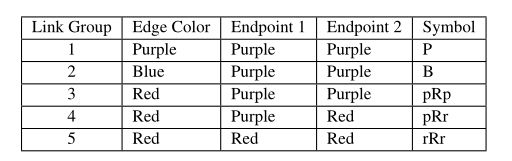
图2.酵母2K与SC的完美配对。上图：全网络视图。底部：具有紫色(P)和蓝色(B)边的子网的详细信息。五个链接组由浅色和深色的交替带表示；每个节点组都从BioFabric的标准节点注释调色板中指定固定的颜色。为清楚起见，此处沿网络顶部添加了每个链路组的超大标签。如正文中所述，可以使用每个链路组的宽度来直观地估计诸如S3、EC和ICS之类的用于对齐质量的公共拓扑测量。例如，S3是最左边的三个链路组P、B和PRP之和上的最左边的链路组P的宽度，即大约1/4(实际值：0.248)。

2.7 与BioFabric的接口

BioFabric Version2(现在处于测试版)提供了一个新的插件架构，允许开发人员向程序中添加新功能。插件是用Java编写的，当包含编译后的代码的.jar文件放在用户指定的目录中时，BioFabric的Tools菜单中就可以使用新功能。我们的VISNAB插件使用此新架构来提供新功能，允许用户加载两个网络、一个比对文件和一个可选的完美参考比对，然后处理和布局所需的比对视图。该插件还使用了BioFabric版本2中现在引入的新节点和链接注释功能。该功能允许用户指定节点或链接的跨度，然后通过在背景中绘制彩色矩形来突出显示这些节点或链接。

3 结果

案例研究I：可视化黄金标准对齐

即使用户确切地知道两个网络是如何排列的(例如，节点是来自同一生物体的蛋白质，而网络来自两个不同的研究)，能够直观地解释这两个网络的比较也是非常有价值的。BioFabric使比较任何两个网络变得容易，我们新的节点和链路组定义可以应用于这些比较。

图2显示了一个网络，其中网络酵母2K已经与网络SC完美地对齐。较大的SC网络来自酿酒酵母，包含5831个节点和77,149条边，最初从BioGRID(v3.2.101,2013年6月)获得(Chatraryamontri等人，2013年)。更小的酵母2K网络，也来自酿酒酵母，是从最初从Collins等人的数据中产生的具有2390个节点和16,127条边的网络中衍生出来的。(2007)，并在Kuchaiev等人中使用。(2010年)。补充资料中提供了如何为这两个使用不同蛋白质标识符的网络生成完美比对的细节，以及如何修剪原始酵母2K以实现完美比对。

图2的顶部显示了整个网络，而底部的详细信息显示了具有紫色和蓝色边缘的子网。此显示使用最近添加的BioFabric版本2功能：节点和链接注释显示。详图中可见的主色带表示节点组(P：P/PRP/PRR)(粉色)、(P：B/PRP/PRR)(粉蓝色)和(P：P/B/PRP/PRR)(黄色)。请注意，细节的紫色边缘区域的淡蓝色带中没有节点；这些节点只有蓝色和红色的入射边。因此，(P：B/PRP/PRR)带中的节点开始于细节的(B)区域。

请注意，5个链路组和20个节点组如何快速揭示这一黄金标准对齐的本质。我们立即看到，更大的网络中的节点数量是原来的两倍多。最左边的两个阴影链路组频带(P和B)中的边正好表示原始网络中的链路；而沿着(P：P/B/PRP/PRR)(黄色)节点组向下的彩色频带中的紫色节点是该较小网络中的所有节点。如果将较大的网络视为较晚、更完整、更准确的调查，则B组中的边缘代表较早调查的假阳性。中间链路组PRP中的红边是作为原始调查的一部分的节点之间的新边，而PRR和RRR链路组中右边40%的边表示入射到至少一个新的红色节点上的新边。

案例研究II：可视化公共拓扑测度

有几种方法可以评估路线的拓扑质量。根据上下文的不同，这些测量量化两个PPI网络在拓扑上的相似程度。设EA={(U1，U2)∈E1：(a(U1)，a(U2))∈E2}表示G1中与G2中的边对齐的边。边覆盖(EC1)是较小网络中与较大网络中的边对齐的边的比例：EC(A)=|EA|/|E1|。设ˆEA={(v1，v2)∈E2：∃u1，u2∈v1∧a(U1)=v1∧a(U2)=v2}表示G2在其对齐节点上诱导的边集。诱导保守结构(ICs)是对齐边与诱导边的比值：ICs(A)=|Ea|/|ˆEa|。然而，EC和ICS的缺点是，如果对齐将一个网络的稀疏区域映射到另一个网络的密集区域，则它们可能较高。在极端情况下，如果G2是一个集团，则任何对齐都有Ec=1。为了克服这一缺点，Saraph和Milenkovi‘c(2014)设计了对称子结构得分(S3)，即对齐的边与具有对齐的端点节点的所有边的比率：

由于BioFabric在绝对规则的网格上布置节点行和链接列，因此各种节点和链接组的宽度比例允许用户快速直观地看到这些拓扑度量。例如，可以通过将第一个链路组(紫边)的宽度与前三个链路组(紫色节点之间的所有链路)的宽度进行比较来估计S3：

查看图2的顶视图，我们直观地估计此对齐的S3得分约为1/4(实际值：0.248)。同样，EC是紫色链接组在紫色和蓝色链接组宽度上的宽度：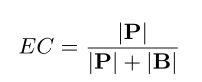

我们可以直观地估计EC约为2/3(实际值：.689)。最后，ICS是紫色链接组的宽度除以带有紫色端点节点的紫色组和红色组的宽度：

我们可以直观地估计ICS在3/10左右(实际值：0.280)。因此，BioFabric的节点和链接组提供了抽象拓扑测度的直观。

案例研究III：目标函数的可视化执行

选择应用于特定网络对齐的最佳目标函数目前是一门黑术，为研究人员提供帮助了解各种目标函数的属性和性能的可视化工具有助于深入了解这一难题。

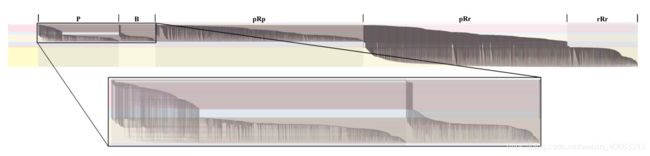
事实上，BioFabric关于网络排列的陈述让研究人员可以做到这一点。图3描述了前面介绍的酵母2K和SC网络之间的四种比对。图的第一行与图2所示的黄金标准正确对齐相同。下面的三对齐是通过运行SANA(Mamano和Hayes，2017)各10小时，优化以下目标函数而生成的：第二行对齐是使用仅利用重要性(I)的目标函数生成的(Hashemifar和Xu，2014)；第三行对齐赋予S3 0.03权重，i赋予0.97权重；第四行仅利用S3。

除了查看四个比对的BioFabric图之外，我们还可以查看针对它们的新的NGS、LGS和JS度量，以及传统的NC、S3和Resnik语义相似性得分(Resnik，1995；Lord等人，2003a，b)。这些分数如表3所示。最高的S3值和最高的NC值通常是用来识别“最佳”比对的度量。如表所示，纯S3版本在这两个版本中得分最高。然而，这个“最好”的NC分数只有2.1%，这并不是一个很鼓舞人心的结果。即使我们新的JS得分6.9%，可以容忍拓扑相似的错配，也仍然很低。

表3.酵母2K和SC之间四种比对的得分。

简单地看一下图3中的四个BioFabric图就会让我们质疑，称纯S3版本是这两个网络的“最佳”对齐。回想一下，S3是第一个链接组的宽度超过前三个链接组的宽度，我们可以立即看到：(I)纯S3版本的值比任何其他对齐方式都要高得多，即使是正确的对齐方式，并且(Ii)它通过创建一种对齐方式来实现这一点，该对齐方式将更多的边强制到最右边的两个链接组PRR和RRR中。特别令人担忧的是，与完美对齐相比，RRR的大小增加了很多；该集表示从对齐中完全省略的边和节点。

高度节点被降级为红色未触及节点这一事实为改善这种情况提供了线索。也许使用重要性(其中最高程度的节点往往彼此对齐)作为目标函数可以解决这个问题？这种方法产生了图3第二行中的“纯重要性”版本。实际上，该版本右端的链接组PRR和RRR似乎在大小上更接近正确的对齐，中心链接组PRP也更接近正确的对齐，尽管更大。但是最左边的一组紫色P边太薄了，几乎不存在。因此，纯重要性产生的S3值仅为0.0043。

那么，也许两个目标函数的简单线性混合可以在这两个极端之间提供折衷？为了研究这一点，我们运行了一系列的比对运行，使用两个目标函数的线性混合，并对9个组合进行了评分。所有九个项目的分数都包含在补充材料中。混合物(.03∗S3)+(.97∗I)显示在第三行，就五个链接组之间的边缘分布而言，它提供了黄金标准对齐的合理视觉匹配。这种视觉相似性也体现在表3中所示的度量中。扫描各种混合值时，该特定混合产生了与高NGS、相当高的LGS、非零NC和可接受的JS值的对齐。它也有最接近黄金标准的S3值，加上最高的功能相似性，即根据Resnik评分，在所有的比对中，生物相关性最高。

图3.用酵母2K和SC之间的四个比对直观地评估不同目标函数的性能。第一行：金标；第二行：1.0∗I(仅限重要性)；第三行：混合(.03∗S3)+(.97∗I)；第四行：1.0∗S3。在每个连续行的对齐中，我们已经绘制了跟随从第一行对齐到相应链接组的每个链接组的线。第二行中的对齐明显比其他行宽，因为对齐的P条边代表原始网络对中的两条边，而该对齐具有非常少的P条边。

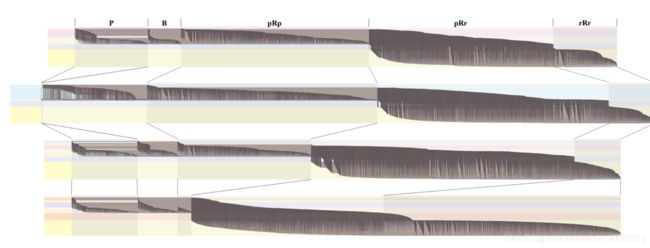
图4.使用对齐周期布局排列的有问题的Yeast0到Yeast20对齐的完整视图。启用了BioFabric阴影链接(Longabaugh，2012)。未正确对齐的节点的对齐周期用交替的橙色和绿色块表示。编号框突出显示包含下图中显示并在文本中讨论的单周期、两周期和四周期集群工件的(非连续)部分。

案例研究IV：发现蛋白质簇错位

虽然查看特定路线的度量值可以大致了解路线的执行情况，但能够快速发现可用黄金标准路线的路线中的主要问题，然后能够了解问题所在，这是有价值的。

图4显示了一个酵母网络Yeast0，它由1,004个节点和8,323条边组成，与具有相同节点集的网络对齐，但是多了20%(9,987)条边，Yeast20。这个网络是Collins等人网络上嘈杂酵母变体的一部分。(2007)。较小网络中的边是较大集合的严格子集。该数据集已用于之前的几项研究(Patro和Kingsford，2012；Saraph和Milenkovi‘c，2014；Mamano和Hayes，2017)。我们在这里使用的特殊排列是SANA(Mamano and Hayes，2017)生成的组合的一部分，但与组合中的其他排列相比是异常糟糕的；这让我们想知道，这个糟糕的排列有什么不同？此可视化是使用与第2.3节中描述的相同网络合并技术创建的。该网络中的节点被标记为表示对准结果，例如a：：A表示正确的对准，而a：：B表示不正确的对准。边缘标记为P(紫色边缘)、B(蓝色)或PRP(红色)。

为了能够发现路线问题，我们使用新的路线周期布局方法查看网络，如第2.6节所述。此布局不会将节点划分为节点组，但仍会生成链接组。由于两个网络的节点集相同，因此没有红色节点，因此只存在三个fivelink组。对于这种类型的表示，我们使用BioFabric的每个节点的链接组布局，将链接分成每个节点的专用节点区域内的三个不同的组。这与我们以前使用的按网络方法形成对比，即为每个链路组创建单个全局区域。

在图4中，大的未着色伸展表示大多数节点，特别是高度高的节点已正确对齐。但是，未对齐的循环(即使是长度为2的循环)显示为使用链接注释功能生成的交替的橙色和绿色块。为了更好地理解这些错位，我们放大每个区域来更仔细地研究它们。

一个有趣的区域包括一个包含15个节点的错位循环，如图5所示。此图底部显示了该循环的一小部分的BioFabric表示。使用Cytoscape(Shannon等人，2003)创建的更熟悉的节点-链接图版本在图的顶部，其中蛋白质相互作用是蓝色的，有方向的红边表示排列。除了图左侧的15个节点的大未对齐周期外，还有长度为2和3的正确对齐和小周期。

这显然是一个单一的蛋白质簇；事实上，它是大亚基的线粒体核糖体蛋白的一些蛋白质成分。(请注意，本文中蛋白质的所有特征都来自Saccharomyces Genome Database(SGD)(Cherry等人，1998)。)。虽然不是完全连接的，但它确实近似于一个集团，因此在目标函数仅使用拓扑的情况下，这里发现的未对齐并不令人惊讶。

最重要的是，我们可以立即用BioFabric版本的网络解释错位的背景：“边缘楔形”的重复模式是当集团中的节点连续布局时，在BioFabric中的迹象。记住，节点行的顺序已经使用对齐周期的顺序来确定，我们看到在这种情况下，节点顺序仍然保持典型的集团模式，因此未对齐实际上包含在集团内。因此，这些在仅拓扑路线中是合理的。

通过展示BioFabric中不重要的错位的正常蛋白质簇/集团来设置上下文之后，我们现在将注意力转向一个更深层次的比对问题，如图6所示。BioFabric表示在上面显示，而传统的节点链接版本在下面。

该未对准在三个对准周期中涉及32个节点。如节点链接版本所示，在这种情况下，比对错误地将一个完整的蛋白质复合体与一个完全不同的复合体对齐了！左边是CPF裂解和多聚腺苷酸因子的蛋白质，右边是RSC染色质重塑复合体的成分。

请仔细注意这个问题在BioFabric版本中是如何突出的，在该版本中，用户通常研究和比较节点的“边缘楔形”形状，以更好地理解网络结构。虽然典型的集团模式(如图5所示)具有下边距为45◦的楔形边，但这些楔形边的下边距更陡，下边距为60◦；在此运行中，每个节点的边实际上都位于交替节点上。对这种模式的解释是，属于两个独立蛋白质簇的节点被插入到使用比对循环布局的这一系列节点中。因此，我们的路线循环布局技术使这个问题仅仅通过观察就变得突出起来。

即使有人会争辩说，传统的节点链接图可视化很好地展示了这些效果，一旦我们知道了我们正在看的是什么，所显示的视图就必须精心手工制作来说明结构，而BioFabric表示是自动布局的。

最后，图7显示了严重的退化，其中四个单独的蛋白质簇错位了！尽管如此，BioFabric对这个问题的描述，使用对齐周期布局，遵循前面所示的相同模式。请记住，对齐循环布局将对齐的节点放置在连续的行中，这些簇中节点的边楔形清楚地显示了已对齐的节点之间的交错边。

图5.线粒体核糖体大亚基的蛋白质，在顶部显示为传统的节点-链接图，蓝色边缘表示蛋白质-蛋白质相互作用，红色边缘表示比对。考虑到节点的高拓扑相似性，未对准是预期的。但是，至关重要的是，此群集中的节点与同一群集中的其他节点对齐。在BioFabric视图(下图)所示的簇的一部分中，具有45◦角的重复“边缘楔形”模式是集团的规范表示。当节点未对准是簇内时，使用对准周期的节点排序没有明显影响。BioFabric视图左侧显示的绿色三元组是位于上方视图2：30位置的循环，而橙色部分是左半部分显示的非常大的循环的一部分。

图6.将此BioFabric图中的“边缘楔形”的形状与图5中的形状进行比较；请注意，楔形的角度为60◦(而不是45◦)，并且在未对齐的节点位于相邻行的情况下，每个节点的边缘入射到交替的节点行上。这是一个明确的视觉提示，表明两个完全不同的蛋白质复合物之间存在错位。传统的节点-链接图显示在右下角，蓝色边缘表示蛋白质-蛋白质相互作用，红色边缘表示比对。请注意所有这些红色节点对齐链接是如何在两侧之间来回交叉的。左侧含有CPF裂解蛋白和多聚腺苷酸因子，右侧含有RSC染色质重塑复合体成分。仔细观察BioFabric细节(左下角)，我们可以看到两个相邻楔体的边是如何入射到不相交的节点集上的。

图7.更引人注目的错位，四种不同的蛋白质复合物以循环方式互换。传统的节点-链接图显示在左下角，蓝色边缘表示蛋白质相互作用，红色边缘表示比对。四个蛋白质复合体从上到下依次为：1)糖酵解和糖异生相关基因，2)甘露糖基转移酶复合体和禁忌素复合体，3)信号识别颗粒，4)辅瘤复合体(COPI)。右下角详细显示的顶部的BioFabric布局显示了此人工产物显示的独特模式，其中相邻的边缘楔形的边缘每四个节点循环一次。请注意，由于构成此结构的三个独立循环在布局中不连续，因此移除了切片。

4 讨论

考虑到使用传统的节点链接图查看网络对齐的质量和特征是困难的，因此研究人员集中精力通过比较和优化某些数值度量来评估对齐也就不足为奇了。但是，为了能够获得一些关于网络比对的广泛直觉，这一研究领域与大多数其他领域没有什么不同，因为拥有有效和组织良好的可视化技术可以在理解问题方面提供巨大的好处。

在提供对节点链接方法的深入直观的同时(尽管节点用线条描绘)，BioFabric还为用户提供了以有意义的方式对节点和边进行分组和排序的能力。这给研究人员提供了一种新的方法来解决理解网络排列的问题。由节点线实现的有组织的边分组是特别独特的。正如我们已经展示的，链接组类别比例的简单视觉估计提供了对S3这样的抽象度量的直观。此外，正如我们的对齐周期布局所展示的那样，可以创建新的专用布局算法，该算法利用节点的线性排序，从而可以快速发现和表征对齐病理。

由于这些特点，BioFabric是研究目标函数及其性能的一个可行的工具。正如Mamano和Hayes(2017)中所讨论的，我们强烈主张网络对齐社区不应将重点放在开发新的网络对齐算法上，而应集中在设计更有效的目标函数上。就像我们尝试将S3和重要性结合起来一样，研究人员应该为他们的特定需求设计定制的目标函数，以产生最优的结果。为了完成这一任务，我们建议将BioFabric作为研究人员应该用来帮助设计目标函数的工具。

Limitations

对于已经习惯于将节点可视化为点的网络研究人员来说，BioFabric将“节点表示为线”并不熟悉，这可能需要一些时间来适应。对于足够小的网络，传统的节点链接图方法就足够了，因此允许用户选择BioFabric网络的子集并使用传统的表示来查看它将是有益的。但此功能目前不可用。

当前VISNAB实施的另一个缺点是，根据表2中的顺序，节点组的顺序是固定的。不同的顺序可能更有助于可视化特定的对齐，因此能够动态重新排序节点组将是一个有用的功能。

最后，就像现有的NC分数一样，我们新的NGS、LGS和JS分数取决于黄金标准对齐的可用性。因此，只有在已知正确答案的情况下，它们才能真正用于评估比对算法和目标函数的性能。为了结合到有用的目标函数中，对于某些类别的比对问题，可以先验估计NGS和LGS分数的目标向量。建立基于增量评价的目标函数的难度也是一个悬而未决的问题。

Future work

在本文中，我们在案例研究III中演示了如何简单地可视化节点和链路类上的节点和边的分布，提出了通过裁剪目标函数来改进对齐的方法；在这种情况下，我们只使用了S3和重要性的简单线性组合。但是，提供允许用户创建更复杂的目标函数组合的工具，然后使用如图3所示的堆叠比较格式来可视化这些选项，将提供探索如何为不同类别的对准问题定制目标函数的强大手段。

另一个新兴的研究领域是多个网络对齐问题，例如Vijayan和Milenkovi(2018)，可视化多个网络对齐具有挑战性。在这些类型的路线中，共享路线中特定边或节点的整个网络集的分数是一条至关重要的信息。这表明为具有相似重叠百分比的元素分组而创建节点和链路组将有助于可视化多网络路线的质量和特征。

我们的新工具提供了一个实现其他新可视化的平台，用于探索网络路线。例如，我们在本文中展示的可视化效果显示了我们在第2.3节中描述的完全合并的网络。然而，构建和可视化整个网络的子图也可以提供有价值的见解。例如，我们支持的另一个视图是孤儿边布局，它显示了G1的子图，其中包含由孤立的蓝色B边连接的所有节点(即表2中的节点组3、5、7、8、11、13、15和16)，以及这些节点的一阶邻居和相应的连接边。请注意，在G1中的边是G2的子集的网络中(例如，案例研究IV中使用的嘈杂酵母网络)，在正确对齐的网络中根本不存在蓝边。因此，查看网络中孤立的蓝色B边的上下文可以深入了解对齐问题。

以类似的方式，我们可以创建许多其他类型的视图，例如通过仅显示对齐的紫色边P的子图及其关联的紫色节点来可视化对齐的公共子图CSA=(V1，EA)的视图。如果此图使用Longabaugh(2012)中描述的BioFabric的默认布局进行布局，则可以评估CSaca的各种连接组件。一般来说，好的排列有一个与大的连通区域共同的子图(Kuchaiev等人，2010年；Saraph和Milenkovi‘c，2014年；Mamano和Hayes，2017年)。因此，用户可以使用连接组件的节点的高度和边的宽度来可视地估计测量最大公共连通子图(LCCS)的组件。

最后，用于装饰节点组和链路组的彩色注释块本身可以单独使用(不显示实际网络)，以提供跨类对齐中的节点和边分布的快速概览。请注意，这些块的相对高度和宽度才有意义，因此此方法甚至可以应用于平均节点度非常高的大型网络。在这种情况下，这种网络(平均程度高的网络在BioFabric中非常长而不高)的极高纵横比不会成为障碍，因为可以统一缩放链接组以创建低纵横比视图，同时保持正确的比例。