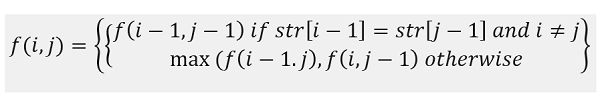最长不重复子序列_最长重复子序列
最长不重复子序列
Description:
描述:
This question has been featured in interview rounds of Amazon.
这个问题已在亚马逊的采访回合中提到。
Problem statement:
问题陈述:
Given string str, find the length of the longest repeating subsequence such that the two subsequences don't have the same character in the same position, i.e., any ith character in the two sub-sequences shouldn't have the same index in its original string.
给定字符串str ,求出最长重复子序列的长度,以使两个子序列在相同位置没有相同的字符,即,两个子序列中的任何第 i 个字符在其位置均不应具有相同的索引原始字符串。
Let the string be,
Str="includehelpisbest"
Output will be:
Longest repeating sub-sequence length is 3
The longest repeating sub-sequence is:"ies"
The output is given above where the repeating sub-sequences are in two different colours. One more repeating subs-sequence can be,
上面给出了输出,其中重复子序列使用两种不同的颜色。 可以再重复一个子序列,
Solution Approach:
解决方法:
The problem can be solved in similar way as longest Common subsequence problem, where input to LCS() would be String str both the case. That is
可以通过与最长公共子序列问题类似的方法来解决该问题 ,在这两种情况下, LCS()的输入均为String。 那是
LRS(str) = LCS(str,str) which some constraints
Let's discuss the recursive approach first.
让我们首先讨论递归方法。
Let,
让,
l = Length of the string,str
f(l,l) = Longest repeating subsequence length for string length l
Now,
现在,
Think of the following example,
考虑以下示例,
Say the string is: x1x2...xl
假设字符串是: x 1 x 2 ... x l
Say,
说,
xi==xj and i≠j (this is the constraint what we discussed above)
x i == x j和i≠j (这是我们上面讨论的约束)
Then obviously we need to find LCS for the remaining part of string (x1x2...xi-1, x1x2...xj-1) and then add 1 for this valid character match (repeating character match),
那么显然我们需要为字符串的其余部分(x 1 x 2 ... x i-1 ,x 1 x 2 ... x j-1 )找到LCS,然后为这个有效的字符匹配添加1(重复字符比赛),
Else
其他
Maximum of two case,
最多两种情况
LCS of the string leaving character xi,x1x2...xi-1 and string x1x2...xj.
字符串x i ,x 1 x 2 ... x i-1和字符串x 1 x 2 ... x j的 LCS。
LCS of the string xl1, x1x2...xi and second string leaving character xj,x1x2...xj-1
字符串x l 1 ,x 1 x 2 ... x i的 LCS和第二个字符串剩下的字符x j ,x 1 x 2 ... x j-1
Now, we need to recur down to 0. So,
现在,我们需要递归降至0。因此,
Where base cases are,
在基本情况下,
f(0,i)=0 for 0≤i≤l
f(i,0)=0 for 0≤i≤ l
If you generate this recursion tree, it will generate many overlapping sub-problems and thus, we need to reduce the re-computing. That's why we need to convert it into dynamic programming where we will store the output of the sub-problems and we will use it to compute bigger sub-problems.
如果生成此递归树,它将生成许多重叠的子问题,因此,我们需要减少重新计算。 这就是为什么我们需要将其转换为动态编程,以便在其中存储子问题的输出,并使用它来计算更大的子问题。
Converting to Dynamic programming:
转换为动态编程:
1) Initialize dp[l+1][l+1] to 0
2) Convert the base case of recursion:
for i=0 to l
dp[i][0]=0;
for i=0 to l
dp[0][i]=0;
3) Fill the DP table as per recursion.
for i=1 to l //i be the subproblem length for first string of LCS
for j=1 to l //j be the subproblem length for second string of LCS
if(i≠j and str1[i-1]==str2[j-1]) //xi==xj and i≠j
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
end for
end for
4) The final output will be dp[l][l]
C++ Implementation:
C ++实现:
#include
using namespace std;
void print(vector a, int n)
{
for (int i = 0; i < n; i++)
cout << a[i] << " ";
cout << endl;
}
int max(int a, int b)
{
return (a > b) ? a : b;
}
int LRS(string str1, string str2)
{
int l = str1.length();
int dp[l + 1][l + 1];
//base case
for (int i = 0; i <= l; i++)
dp[i][0] = 0;
for (int i = 0; i <= l; i++)
dp[0][i] = 0;
//fill up
for (int i = 1; i <= l; i++) {
for (int j = 1; j <= l; j++) {
if (i != j && str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[l][l];
}
int main()
{
string str;
cout << "Enter the string:\n";
cin >> str;
cout << "Longest repeating sub-sequence length: " << LRS(str, str) << endl;
return 0;
}
Output
输出量
Enter the string:
includehelpisbest
Longest repeating sub-sequence length: 3
翻译自: https://www.includehelp.com/icp/longest-repeating-subsequence.aspx
最长不重复子序列