力扣1514——概率最大的路径
本题主要和图的遍历求解最短路径相关,可以用 Dijkstra 或者 Bellman-Ford 算法进行解决。
原题
给你一个由 n 个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end ,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ,就会被视作正确答案。
示例 1:
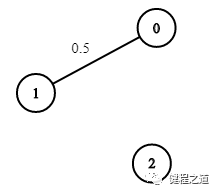
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出:0.25000
解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25
示例 2:
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出:0.30000
示例 3:
输入:n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出:0.00000
解释:节点 0 和 节点 2 之间不存在路径
提示:
2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边
解题
首次尝试
原本,我想利用树的深度优先搜索遍历,加上一定程度的剪枝(就是排除已经遍历过的节点),完成这道题目,代码如下:
class Solution {
/**
* key为起始点,value为所有相连的点
*/
Map> map;
/**
* key为"点A_点B"(A < B),value为对应的概率
*/
Map probMap;
double maxProb = -1;
int end;
public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
map = new HashMap<>(n * 4 / 3 + 1);
probMap = new HashMap<>(succProb.length * 4 / 3 + 1);
this.end = end;
// 构造每个点的相连关系
for (int i = 0; i < edges.length; i++) {
int[] edge = edges[i];
Set set = map.computeIfAbsent(edge[0], k -> new HashSet<>());
set.add(edge[1]);
set = map.computeIfAbsent(edge[1], k -> new HashSet<>());
set.add(edge[0]);
String key = edge[0] < edge[1] ? (edge[0] + "_" + edge[1]) : (edge[1] + "_" + edge[0]);
probMap.put(key, succProb[i]);
}
boolean[] visited = new boolean[n];
dp(start, 1, visited);
return maxProb == -1 ? 0 : maxProb;
}
public void dp(int index, double prob, boolean[] visited) {
// 已到终点
if (index == end) {
maxProb = prob > maxProb ? prob : maxProb;
return;
}
// 获取当前点可以到达的所有点
Set set = map.get(index);
// 如果当前点到达不了其余点
if (set == null) {
return;
}
// 标记当前点已访问
visited[index] = true;
// 遍历相邻的点
for (int next : set) {
if (visited[next]) {
continue;
}
String key = index < next ? (index + "_" + next) : (next + "_" + index);
// 访问下一个点
dp(next, prob * probMap.get(key), visited);
}
// 退出,将该点标记为未访问
visited[index] = false;
}
}
但很可惜,超时了。我想了一下,应该是因为没有借用之前已经计算出来的结果,因此比较浪费时间。
其时间复杂度取决于边的数量,假设边的数量是 m ,则时间复杂度为O(m^2)。
而边 m 与点 n 的关系,m 最小是 0(也就是点之间没有线),最大是 (n - 1) * n / 2,每个点之间都有连线。
因此可以预见,这样的算法效率确实很差。
Dijkstra 算法
定义概览
Dijkstra (迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
注意该算法要求图中不存在负权边。
算法思想
设 G=(V,E) 是一个带权有向图,把图中顶点集合 V 分成两组:
第一组为已求出最短路径的顶点集合(用 S 表示,初始时 S 中只有一个源点,以后每求得一条最短路径 , 就将加入到集合 S 中,直到全部顶点都加入到 S 中,算法就结束了)。
第二组为其余未确定最短路径的顶点集合(用 U 表示),按最短路径长度的递增次序依次把第二组的顶点加入 S 中。
在加入的过程中,总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S 中的顶点的距离就是从 v 到此顶点的最短路径长度。U 中的顶点的距离,是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。
算法步骤
初始时,S 只包含源点,即 S ={v},v 的距离为0。U 包含除 v 外的其他顶点,即: U ={其余顶点},若 v 与 U 中顶点 u 有边,则
正常有权值,若u不是v的出边邻接点,则权值为∞。从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
重复步骤b和c直到所有顶点都包含在S中。
执行动画过程如下图
本题解法
class Solution {
public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
// records[i]代表点i相邻的所有点,以及其概率
List> allRecords = new ArrayList<>(n + 1);
for (int i = 0; i < n + 1; i++) {
allRecords.add(new LinkedList<>());
}
// 构造每个点的相连关系
for (int i = 0; i < edges.length; i++) {
int[] edge = edges[i];
List records = allRecords.get(edge[0]);
records.add(new Record(edge[1], succProb[i]));
records = allRecords.get(edge[1]);
records.add(new Record(edge[0], succProb[i]));
}
// 利用广度优先搜索,进行遍历
// 借用优先队列,保证优先遍历当前概率高的
PriorityQueue queue = new PriorityQueue<>();
// 记录从start到每一个点的概率
double[] result = new double[n];
// 从start开始遍历
queue.offer(new Record(start, 1));
result[start] = 1;
// 开始
while (!queue.isEmpty()) {
// 当前节点
Record record = queue.poll();
int node = record.node;
double prob = record.prob;
// 获取当前点所能达到的其他节点
List otherNodes = allRecords.get(node);
// 遍历其余节点
for (Record next : otherNodes) {
int nextNode = next.node;
double nextProb = prob * next.prob;
// 如果当前计算出的概率,小于等于之前计算的概率
if (nextProb <= result[nextNode]) {
// 那么就没有必要继续算了,直接用之前的即可
continue;
}
// 更新概率
result[nextNode] = nextProb;
// 如果已到结尾或者当前的概率已经比到end的小
if (nextNode == end || nextProb < result[end]) {
// 那么也没有必要继续了
continue;
}
// 添加节点
queue.offer(new Record(nextNode, nextProb));
}
}
return result[end];
}
class Record implements Comparable {
int node;
double prob;
public Record(int node, double prob) {
this.node = node;
this.prob = prob;
}
@Override
public int compareTo(Record other) {
if (other == null) {
return -1;
}
if (this.prob == other.prob) {
return this.node - other.node;
}
return this.prob - other.prob > 0 ? -1 : 1;
}
}
}
提交OK,执行用时超过了69%的 java 提交记录,看来还有值得优化的地方。
假设边的数量为 m ,点的数量为 n ,则时间复杂度为O(n + m + nlogn)。
Bellman-Ford 算法
之前有说到 Dijkstra 算法要求不能有负权边,而这个 Bellman-Ford 算法是支持的。
算法步骤
创建源顶点 v 到图中所有顶点的距离的集合 distSet,为图中的所有顶点指定一个距离值,初始均为 Infinite,源顶点距离为 0;
计算最短路径,执行 V - 1 次遍历;对于图中的每条边:如果起点 u 的距离 d 加上边的权值 w 小于终点 v 的距离 d,则更新终点 v 的距离值 d;
检测图中是否有负权边形成了环,遍历图中的所有边,计算 u 至 v 的距离,如果对于 v 存在更小的距离,则说明存在环;
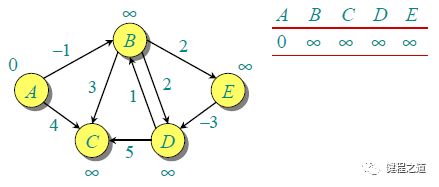
例如,下面的有向图 G 中包含 5 个顶点和 8 条边。假设源点 为 A。初始化 distSet 所有距离为 INFI,源点 A 为 0。
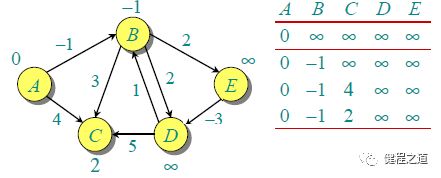
由于图中有 5 个顶点,按照步骤 1 需要遍历 4 次,第一次遍历的结果如下。
第二次遍历的结果如下。
以此类推可以得出完全遍历的结果。
本题解法
class Solution {
public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
// 记录结果
double[] result = new double[n];
// 起点
result[start] = 1;
// 从start点出发,先更新直接与start点相连的点的概率,然后逐步更新,直到不需要更新为止
while (true) {
// 是否有过变动
boolean changed = false;
// 遍历所有边
for (int j = 0; j < edges.length; j++) {
int[] edge = edges[j];
// 如果从当前点edge[0]出发,到edge[1]的概率,大于之前记录的结果
if (result[edge[0]] * succProb[j] > result[edge[1]]) {
// 则更新
result[edge[1]] = result[edges[j][0]] * succProb[j];
changed = true;
}
// 因为是无向图,所以再反向遍历
if (result[edge[1]] * succProb[j] > result[edge[0]]) {
result[edge[0]] = result[edge[1]] * succProb[j];
changed = true;
}
}
// 一遍未修改则表示图已遍历完成
if (!changed) {
break;
}
}
return result[end];
}
}
提交OK,执行用时超过了95%的 java 提交记录。
其时间假设边的数量为 m ,点的数量为 n ,则时间复杂度为O(mn)。
总结
以上就是这道题目我的解答过程了,不知道大家是否理解了。本题主要和图的遍历求解最短路径相关,可以用 Dijkstra 或者 Bellman-Ford 算法进行解决。
有兴趣的话可以访问我的博客或者关注我的公众号、头条号,说不定会有意外的惊喜。
https://death00.github.io/
公众号:健程之道
![]()
点此评论