201709-5 试题名称: 除法
问题描述
小葱喜欢除法,所以他给了你N个数a1, a2, ⋯, aN,并且希望你执行M次操作,每次操作可能有以下两种:
给你三个数l, r, v,你需要将al, al+1, ⋯, ar之间所有v的倍数除以v。
给你两个数l, r,你需要回答al + al+1 + ⋯ + ar的值是多少。
输入格式
第一行两个整数N, M,代表数的个数和操作的次数。
接下来一行N个整数,代表N个数一开始的值。
接下来M行,每行代表依次操作。每行开始有一个整数opt。如果opt=1,那么接下来有三个数l, r, v,代表这次操作需要将第l个数到第r个数中v的倍数除以v;如果opt = 2,那么接下来有两个数l, r,代表你需要回答第l个数到第r个数的和。
输出格式
对于每一次的第二种操作,输出一行代表这次操作所询问的值。
样例输入
5 3
1 2 3 4 5
2 1 5
1 1 3 2
2 1 5
样例输出
15
14
评测用例规模与约定
对于30%的评测用例,1 ≤ N, M ≤ 1000;
对于另外20%的评测用例,第一种操作中一定有l = r;
对于另外20%的评测用例,第一种操作中一定有l = 1 , r = N;
对于100%的评测用例,1 ≤ N, M ≤ 105,0 ≤ a1, a2, ⋯, aN ≤ 106, 1 ≤ v ≤ 106, 1 ≤ l ≤ r ≤ N。
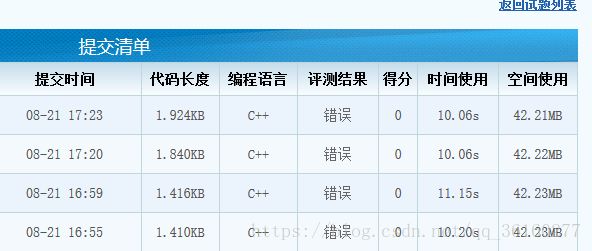
WA代码
wa掉是我用了自己造的一棵树,错了。
#include
#include
#include
#include
using namespace std;
class Position{
public:
int c,t;//层数 位置
};
vector tree[18][100005];
vectorps;
int a[100005];
int allC,n,m;
void find(int l,int r){
int c=floor(log(r-l+1)/log(2));//当前层数
int cb=pow(2,c);//当前层数上,每一块区间的大小
if(r-l+1==cb&&r%cb==0){//找到的标志
// cout<>n>>m;
allC=ceil(log(n)/log(2));
for(int i=1;i<=n;++i)scanf("%d",&a[i]);
while(m--){
int opt,l,r,v;
scanf("%d",&opt);
if(opt==1){
ps.clear();
cin>>l>>r>>v;
find(l,r);
for(int i=0;i>l>>r;
int sum=0;
for(int i=l;i<=r;++i){
int cb=1;
int num=a[i];
for(int c=0;c<=allC;++c,cb*=2){
int t;
if(i%cb==0){
t=i/cb;
}else{
t=i/cb+1;
}
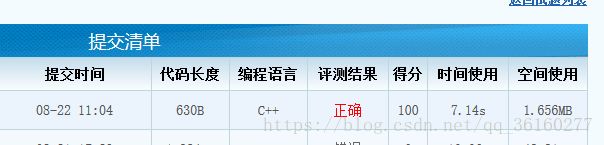
for(int j=0;j AC代码
内容参考于https://blog.csdn.net/gl486546/article/details/78359480
强烈建议学一下树状数组,用百度百科就行!
#include
#include
using namespace std;
long long tree[101024];
int n,m,a[101024];
void update(int i,int val){
while(i<=n){
tree[i]+=val;
i+=-i&i;
}
}
long long getsum(int i){
long long sum=0;
while(i>0){
sum+=tree[i];
i-=-i&i;
}
return sum;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
update (i,a[i]);
}
for(int i=1;i<=m;i++){
int opt,l,r,w;
cin>>opt>>l>>r;
if(opt==2){
cout<>w;
if(w==1)continue;
while(l<=r){
if(a[l]>=w&&a[l]%w==0){
update(l,-(a[l]-a[l]/w));
a[l]/=w;
}
++l;
}
}
}
} 。