【统计学习方法 • 从无到有系列】— 【三】k 近邻算法 kNN

• 本文收录于Github仓库，欢迎前来 star 呀~ https://github.com/Veal98/CS-Wiki
• ‍ 在线阅读地址/更好的阅读体验请移步：https://veal98.gitee.io/cs-wiki/
  

k 近邻算法 kNN

---

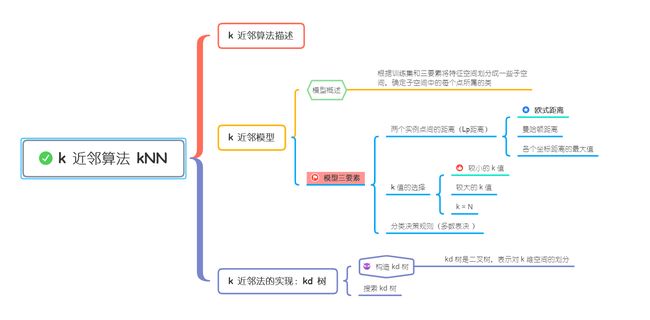
思维导图

1. k 近邻算法描述

✅ k 近邻算法 k-nearest neighbor, kNN 可简单描述为：存在一个带标签的训练样本集，输入没有标签的新数据后，将新数据的每个特征和样本集中的数据对应的特征进行比较，然后算法提取样本集中 k 个特征最相似（最邻近）的分类标签（这就是 k-近邻算法中 k 的 出处，一般 k 不大于 20）。最后，选择这 k 个最相似数据中出现次数最多的分类，作为新数据的分类。

k 近邻法是基本且简单的分类与回归方法，此处我们只考虑分类问题中的 k 近邻法，k 近邻算法是一个可以取多类的分类方法

举个 kNN 算法的直观例子如下：

❓ 假如有一部未看过的电影，如何确定它是爱情片还是动作片呢？

下图显示了 6 部电影的打斗和接吻镜头数，？ 就是我们要判断的电影：

计算未知电影与样本集中其他电影的距离（此处暂时不要关心如何计算得到这些距离，下文会详细讲解）

假定 k = 3，则最靠近的三个电影分别是 He's Not Really into Dudes，Beautiful Woman，California Man，这三部电影都是爱情片，所以我们判断未知电影是爱情片。

2. k 近邻模型

① 模型概述

k 近邻法中，根据训练集和模型三要素（距离度量即两个实例点之间的距离，k 值，分类决策规则）可以将特征空间划分成一些子空间，确定子空间中的每个点所属的类。

特征空间中，对每个实例点，距离该点比其他点更近的所有点组成一个区域，叫作单元 cell。每个训练实例拥有一个单元。

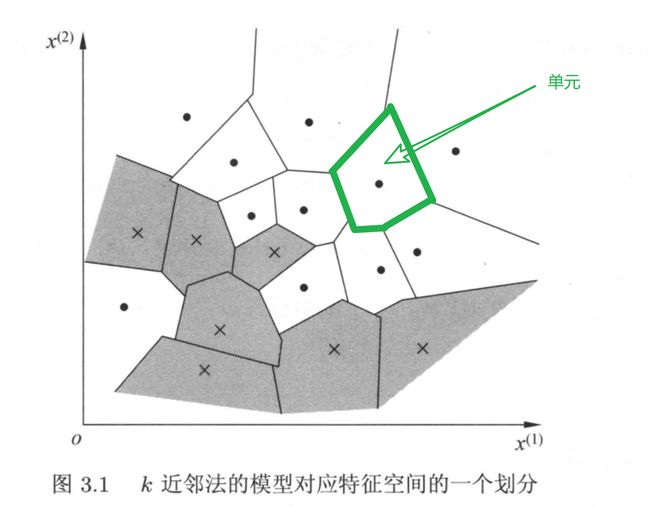
② 模型三要素

Ⅰ 距离度量

✅ 所谓距离度量就是两个实例点之间的距离计算方法，常用的距离是欧式距离。也可以是其他距离，比如更一般的 $L_p$ 距离：

$p=\infty$ 时的距离也称为 切比雪夫距离

计算 $L_p$ 距离的 Python 3 代码实现如下：

import math

# 计算点 x 和 y 之间的 Lp 距离（默认是欧式距离）
def L(x, y, p=2):
    # 最少是二维空间
    if len(x) == len(y) and len(x) > 1:
        sum = 0
        for i in range(len(x)):
            sum += math.pow(abs(x[i] - y[i]), p)
        return math.pow(sum, 1 / p)
    else:
        return 0

‍ 测试该代码：

下图给出了二维空间中取值不同时，与原点的 $L_p$ 距离为 1 （$L_p=1$） 的点的图形：

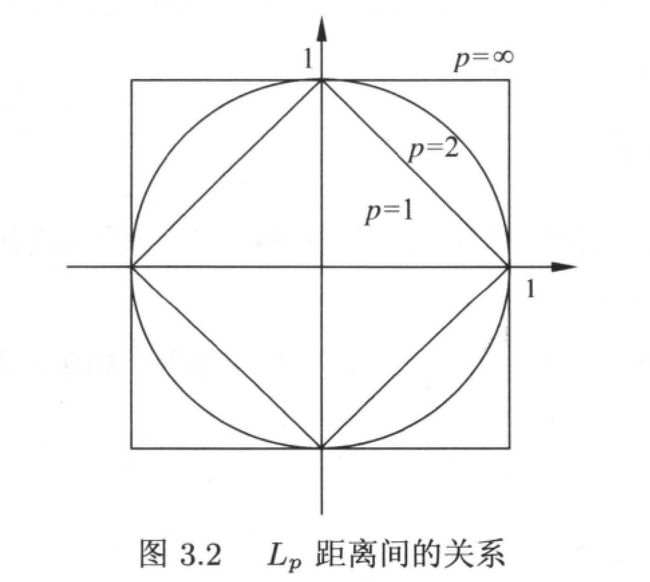
显然，不同的距离度量所确定的最近邻点是不同的， 如下例所示：

编写代码验证上例：

x1 = [1, 1]
x2 = [5, 1]
x3 = [4, 4]

for i in range(1, 5):
    for c in [x2,x3]:
         print('[1,1] 与 {} 之间的 L_{} 距离为：{}'.format(c,i,L(x1,c,p=i)))
    print('\n')

Ⅱ k 值的选择

k 值的选择会对 k 近邻法的结果产生重大影响：

• 如果选择较小的 k 值：相当于用较小的邻域中的训练实例进行预测，学习的近似误差 approximation error会减小，只有与输入实例较近的训练实例才会对结果有影响。缺点是估计误差 estimation error会增大，预测结果会对邻近的实例点非常敏感，如果邻近的实例点是噪声，预测就会出错。

  通俗来说，k 值的减小意味着模型变得复杂，容易发生过拟合。

• 如果选择较大的 k 值：相当于用较大的邻域中的训练实例进行预测，可以减少学习的估计误差，但是缺点是近似误差会增大，因为此时与输入实例较远的训练实例也会对预测结果产生影响。

  通俗来说，k 值的增大意味着模型变得简单。

• 如果 k = N（训练实例的个数）：无论输入实例是什么，都将简单地将其预测为整个训练实例中最多的类。显然这是不可取的

在应用中，一般选取较小的 k 值，通常采用交叉验证法来选取最优的 k 值。

Ⅲ 分类决策规则

k 近邻法中的分类决策规则往往是多数表决：即由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。

3. k 近邻算法的实现 1：线性扫描 linear scan

① 概述

k 近邻法最简单的实现方法是线性扫描 linear scan，即计算输入实例与其他每个训练实例的距离，不过这种方法在训练集很大的时候是不可取的

② 代码详解

以欧式距离为距离度量标准，以多数表决为分类决策规则，基于线性扫描的 kNN 算法的 Python 3 代码如下所示：

def classify(inX,dataSet,labels, k):
    """
    Desc:
        对输入数据点 inx 使用  kNN 算法进行分类
    Args:
        inX: 输入数据点
        dataSet: 训练数据集
        labels: 训练数据集的标签集合
        k: kNN 算法中的 k，即选取 k 个近邻
    """
    dataSetSize = dataSet.shape[0] # 训练数据集中数据的个数
    # 计算输入数据点和训练数据集中各个数据点的欧式距离
    diffMat = np.tile(inX,(dataSetSize, 1)) - dataSet # 计算未知类的数据集与已知数据集的差
    sqDiffMat = diffMat**2 # 差值平方化
    sqDistances = sqDiffMat.sum(axis=1) # 把（未平方根化之前的）未知数据集与两个已知数据的距离分别计算出来
    distances = sqDistances**0.5 # 距离平方根化
    # 对距离进行排序,返回下标
    sortedDistIndicies = distances.argsort() 
    
    classCount = {
     } # 记录 k 个近邻点的类别（标签）
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]] # 遍历排序后的前 k 个标签
        classCount[voteLabel] = classCount.get(voteIlabel,0) + 1 # 记录这 k 个标签出现的次数
    sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True) # 按照出现次数对标签进行从大到小排序
    return sortedClassCount[0][0] # 返回出现次数最多的那个标签

详解如下：

计算输入数据点和训练数据集中各个数据点的欧式距离：

使用欧式距离公式，计算两个向量点 xA 和 xB 之间的距离：

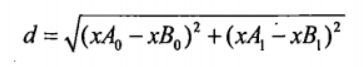
# 计算未知类的数据集与已知数据集的差,为了方便要把未知类的数据集化成矩阵计算
diffMat = np.tile(inX,(dataSetSize, 1)) - dataSet 

np.tile(inX,(dataSetSize, 1)) 将未知类数据 inX 沿着 Y 轴方向扩充 dataSetSize 倍（4 倍），沿着 X 轴扩充 1 倍，即不扩充

举个例子：设未知类数据 inX 是 ([[0,3]]) 即 $\left[\begin{array}{cc}0& 3\end{array}\right]$，数据集 dataSet是 ([[1,3],[3,4]]) 即 $\left[\begin{array}{cc}1& 3\\ 3& 4\end{array}\right]$

将 inx 沿着 Y 轴扩充 2 倍后：$\left[\begin{array}{cc}0& 3\\ 0& 3\end{array}\right]$

计算未知类数据集与已知数据集的差：$\left[\begin{array}{cc}0& 3\\ 0& 3\end{array}\right]-\left[\begin{array}{cc}1& 3\\ 3& 4\end{array}\right]$ = $\left[\begin{array}{cc}-1& 0\\ -3& 1\end{array}\right]$

sqDiffMat = diffMat**2 # 差值平方化

$sqDiffMat={\left[\begin{array}{cc}-1& 0\\ -3& 1\end{array}\right]}^2$ = $\left[\begin{array}{cc}1& 0\\ 9& 1\end{array}\right]$

# 把（未平方根化之前的）未知数据集与两个已知数据的距离分别计算出来
sqDistances = sqDiffMat.sum(axis=1) 

按行向量进行相加：

$sqDistances = [1, 10] $

1 是未知数据与 [1, 3] 的距离，10 是未知数据与 [3, 4] 的距离

distances = sqDistances**0.5 # 距离平方根化

将两个距离分别进行平方根化，分别得到该未知标签向量与已知点的欧式距离

sortedDistIndicies = distances.argsort() # 排序,返回下标

比如说：[3, 5, 1] 从小到大排序分别是：1，3，5，对应的索引是 2，0，1

这样我们在循环的时候, 可以将欧式距离按值从小到大遍历出来

获取距离最近的前 k 个标签出现的次数：

接下来是一个循环，用来记录前 k 个标签分别出现的次数：

classCount = {
     } 
for i in range(k):
    voteIlabel = labels[sortedDistIndicies[i]] # 遍历排序后的前 k 个标签
    classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 # 记录这 k 个标签出现的次数

classCount是一个字典，用来存储标签和标签出现的次数

classCount.get(voteIlabel,0) 返回字典 classCount中 voteIlabel 元素对应的值，若无，则进行初始化为 0，若有，则返回该值

classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1

初始化 classCount = {} 时，此时输入classCount，输出为：
classCount = {}

当第一次遇到新的 label 时，将新的 label 添加到字典 classCount，并初始化其对应数值为 0
然后 +1，即该 label 已经出现过一次，此时输入classCount，输出为：

classCount = {voteIlabel: 1}

当第二次遇到同一个 label 时，classCount.get(voteIlabel,0) 返回对应的数值（此时括号内的 0 不起作用，因为已经初始化过了），然后+1，此时输入classCount，输出为：

classCount = {voteIlabel: 2}

可以看出，+1 是每一次都会起作用的, 因为不管遇到字典内已经存在的或者不存在的，都需要把这个元素记录下来

按照标签出现的次数对标签进行排序：

循环结束后，按照标签出现的次数对标签进行排序：

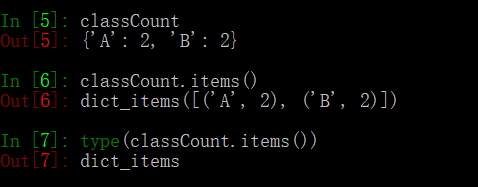
sortedClassCount = sorted(classCount.items(),  key = operator.itemgetter(1), reverse = True) # 按照出现次数对标签进行从大到小排序

classCount.items() 返回的是一个元组 dict_items，即将 classCount转化为元组。例如：

operator.itemgetter(1) 按照第二个元素的次序对元组进行排序（默认从小到大），reverse=True 是逆序，即按照从大到小的顺序排列

返回出现次数最多的标签：

排序完毕后，返回元组中的第一个元素即出现次数最多的标签：

return sortedClassCount[0][0] # 返回出现次数最多的那个标签

③ 运行代码

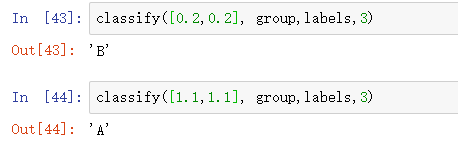
‍ OK，测试一下上述代码：

import numpy as np
import operator # 运算符模块
import matplotlib.pyplot as plt

# 构造数据集
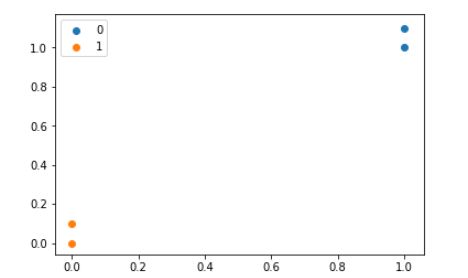
group = np.array([[1.0, 1.1],[1.0, 1.0],[0, 0],[0, 0.1]])
labels = ['A', 'A', 'B' ,'B']

plt.scatter(group[:2,0], group[:2,1], label = '0')
plt.scatter(group[2:4,0], group[2:4,1], label = '1')
plt.legend()

4. k 近邻算法的实现 2：kd 树

① 概述

实现 k 近邻算法时，主要考虑的问题就是如何对训练数据进行快速 k 近邻搜索。

k 近邻法最简单的实现方法是线性扫描 linear scan，这需要计算输入实例与其他每个训练实例的距离，在训练集很大的时候，这种方法是不可取的（上述代码中我们使用的方法都是线性扫描）

为了提高 k 近邻搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数，比如 kd 树

kd 树是二叉树，表示对 k 维空间的一个划分，是一种对 k 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。

② 构造 kd 树

Ⅰ 图解构造 kd 树算法

构造 kd 树相当于不断地用垂直于坐标轴的超平面将 k 维空间切分，构成一些列的 k 维超矩形区域。kd 树的每一个结点对应于一个 k 维超矩形区域。

通常，依次选择坐标轴对空间切分，选择训练实例点在选定坐标轴上的中位数(median)为切分点，这样得到的 kd 树是平衡的。 注意，平衡的 kd 树搜索时的效率未必是最优的。

下面给出构造 kd 树的算法：

举例如下：

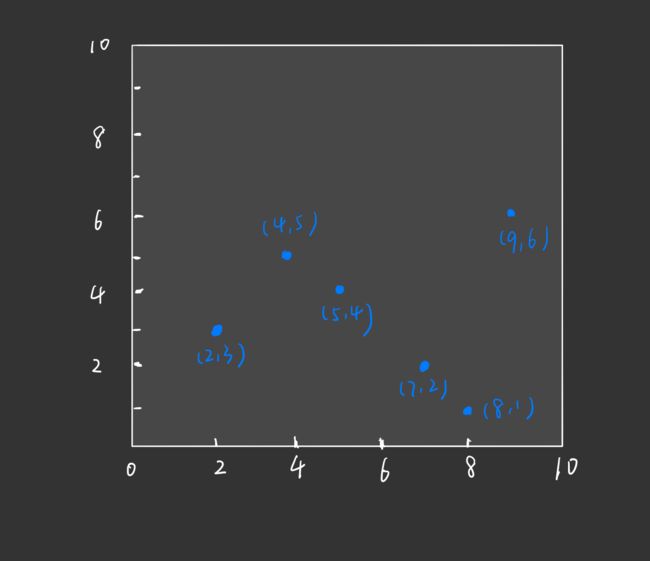
给定一个二维空间的数据集构造一个平衡 kd 树：

详细步骤如下：

• 首先，我们的数据集对应的特征空间如下：

  

• 根节点对应包含数据集 T 的矩形。选择 $x^{(1)}$ 轴，6 个数据点的 $x^{(1)}$ 坐标依次为：$2,5,9,4,8,7$，对应的中位数为 7（中位数本该为 6，但是数据集中没有该数据点，故选 7），即根节点为 $(7,2)$

  ⭐ 通过与 $x^{(1)}$ 垂直的轴即 y 轴进行切分（ $x^{(1)}=7$）， 将空间分为左右两个子矩形：

  

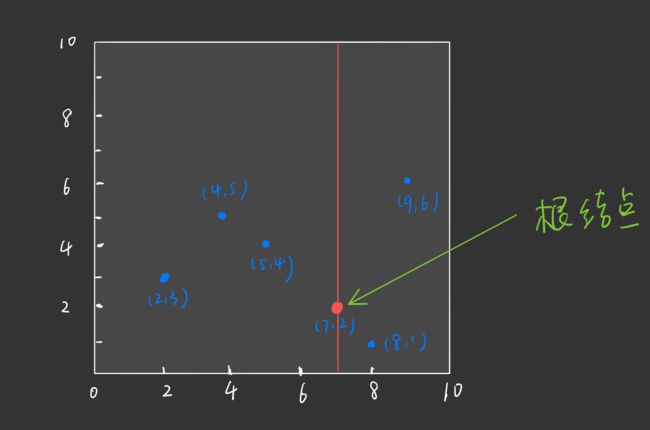
  对应的，构造出的 kd 树如下：

  

• 接着，左矩形以 $x^{(2)}$ 轴 的中位数进行划分。左矩形中拥有的实例点为：$(4,5),(2,3),(5,4)$， 这 3 个数据点的 $x^{(2)}$ 坐标分别为 $5,3,4$，中位数为 4，即根节点的左孩子为 $(5,4)$

  通过与 $x^{(2)}$ 垂直的轴即 x 轴进行切分（ $x^{(2)}=4$）， 将空间分为左右两个子矩形：

  

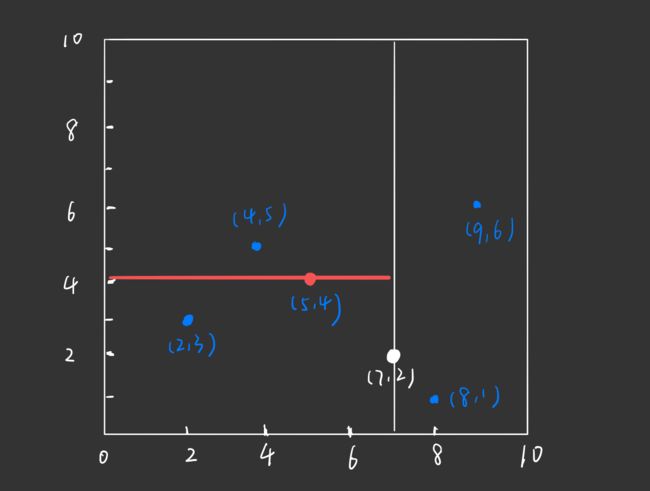
  对应的，构造出的 kd 树如下：

  

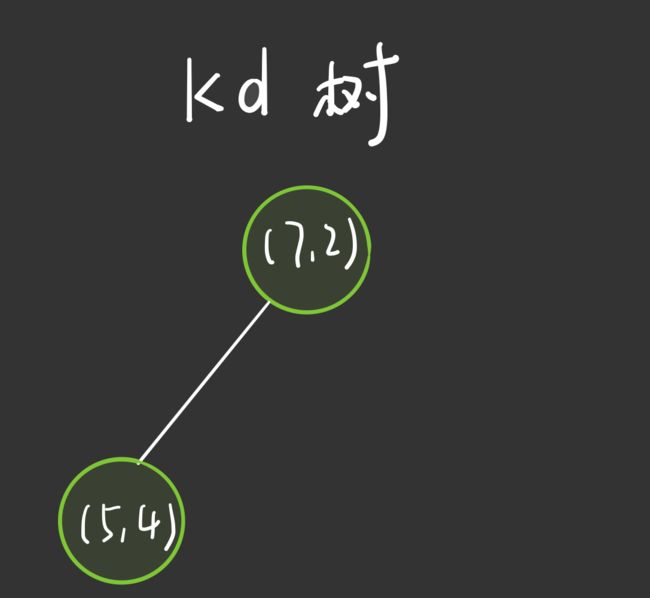
• 同样的，根节点切分出来的右矩形也以 $x^{(2)}$ 轴 的中位数进行划分。右矩形中拥有的实例点为：$(8,1),(9,6)$， 这 3 个数据点的 $x^{(2)}$ 坐标分别为 $1，6$，中位数为 6，即根节点的右孩子为 $(9,6)$

  通过与 $x^{(2)}$ 垂直的轴即 x 轴进行切分（ $x^{(2)}=6$）， 将空间分为左右两个子矩形：

  

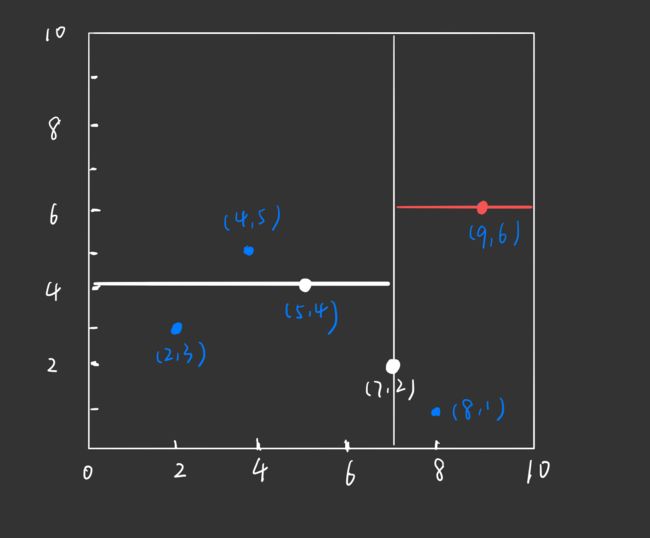
  对应的，构造出的 kd 树如下：

  

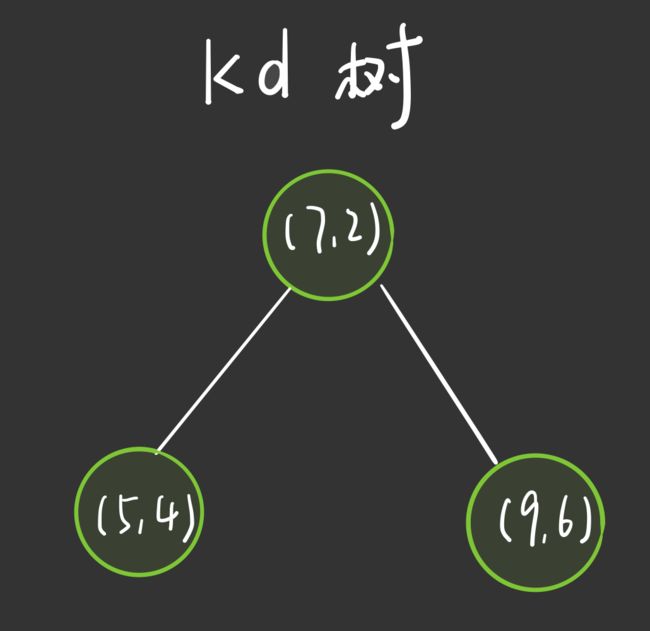
• OK，根节点划分出来的两个子区域处理完了，现在来看根节点的左孩子划分出来的两个子区域，每个子区域中只有一个数据点了：$(2,3)$ 和 $(4,5)$， 上面过程中我们依次按照 $x^{(1)},x^{(2)}$ 进行选取，所以现在又回到了 $x^{(1)}$ (如果有 $ x^{(3)}$ 则按照 $ x^{(3)}$ 进行选取)。

  通过与 $x^{(1)}$ 垂直的轴即 y 轴进行切分（ $x^{(1)}=2$ 和 $x^{(1)}=4$）， 将空间分为左右两个子矩形：

  

  对应的，构造出的 kd 树如下：

  

• 根节点的左孩子划分出来的两个子区域处理完了，现在来处理根节点的右孩子划分出来的两个子区域，只有一个子区域中有数据点 $(8,1)$。

  通过与 $x^{(1)}$ 垂直的轴即 y 轴进行切分（ $x^{(1)}=8$）， 将空间分为左右两个子矩形：

  

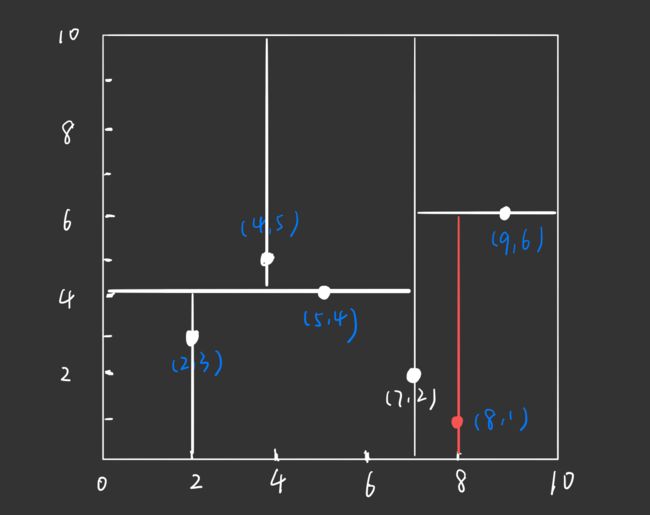
  对应的，构造出的 kd 树如下：

  

  至此，kd 树构造完毕

Ⅱ 代码实现

构造 kd 树算法的具体 Python 代码实现如下：

# kd-tree每个结点中主要包含的数据结构如下
class KdNode(object):
    def __init__(self, dom_elt, split, left, right):
        self.dom_elt = dom_elt  # k维向量节点(k维空间中的一个样本点)
        self.split = split  # 整数（进行分割维度的序号）
        self.left = left  # 该结点分割超平面左子空间构成的kd-tree
        self.right = right  # 该结点分割超平面右子空间构成的kd-tree


class KdTree(object):
    def __init__(self, data):
        k = len(data[0])  # 数据维度

        def CreateNode(split, data_set):  # 按第split维划分数据集exset，并创建KdNode
            if not data_set:  # 数据集为空
                return None
            # key参数的值为一个函数，此函数只有一个参数且返回一个值用来进行比较
            # operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为需要获取的数据在对象中的序号
            #data_set.sort(key=itemgetter(split)) # 按要进行分割的那一维数据排序
            data_set.sort(key=lambda x: x[split])
            split_pos = len(data_set) // 2  # //为Python中的整数除法，求中位数的下标
            median = data_set[split_pos]  # 中位数分割点
            split_next = (split + 1) % k  # 循环选取下一个划分的维度

            # 递归的创建kd树
            return KdNode(
                median,
                split,
                CreateNode(split_next, data_set[:split_pos]),  # 创建左子树
                CreateNode(split_next, data_set[split_pos + 1:]))  # 创建右子树

        self.root = CreateNode(0, data)  # 从第0维分量开始构建kd树,返回根节点


# KDTree的前序遍历
def preorder(root):
    print(root.dom_elt)
    if root.left:  # 节点不为空
        preorder(root.left)
    if root.right:
        preorder(root.right)

‍ 测试一下上述代码：

data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
preorder(kd.root)

③ 搜索 kd 树

Ⅰ 图解搜索 kd 树算法

下面介绍如何利用 kd 树进行 k 近邻搜索。

给定一个目标点，搜索其近邻。首先找到包含目标点的叶节点，然后从该叶节点出发，依次回退到父节点；不断查找与目标点最邻近的节点，当确定不可能存在更近的节点时终止。

显然，利用 kd 树可以省去对大部分数据点的搜索，从而减少搜索的计算量

下面通过一个例题来说明搜索方法：

给定一个如下图所示的 kd 树，根节点为 A，树上共存储 7 个实例点，另有一个输入目标实例点 S，求 S 的最近邻。

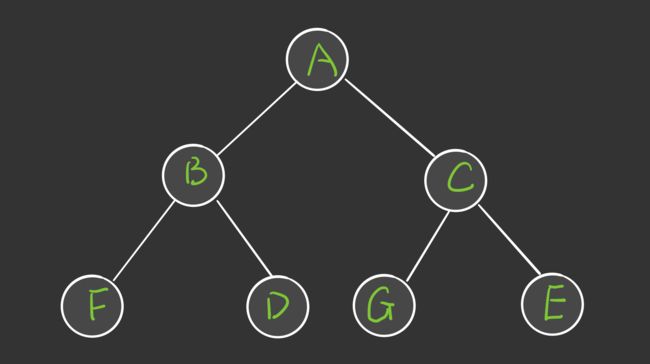
• 首先在 kd 树中找到包含点 S 的叶节点 D，以点 D 作为近似最近邻（ 真正最近邻一定在以点 S 为圆心用过点 D 的圆的内部）
• 然后返回节点 D 的父节点 B，在节点 B 的另一子节点 F 的区域内搜索最近邻。节点 F 的区域与圆不相交，不可能有最近邻点
• 继续返回上一级父节点 A，在节点 A 的另一子节点 C 的区域内搜索最近邻。节点 C 的区域与圆相交，该区域在圆内的实例点有 E，且点 E 比点 D 更近，所以点 E 成为新的最近邻。

Ⅱ 代码实现

搜索 kd 树算法的具体 Python 代码实现如下：

# 对构建好的kd树进行搜索，寻找与目标点最近的样本点：
import math
from collections import namedtuple

# 定义一个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数
result = namedtuple("Result_tuple",
                    "nearest_point  nearest_dist  nodes_visited")


def find_nearest(tree, point):
    k = len(point)  # 数据维度

    def travel(kd_node, target, max_dist):
        if kd_node is None:
            return result([0] * k, float("inf"),0)  # python中用float("inf")和float("-inf")表示正负无穷

        nodes_visited = 1

        s = kd_node.split  # 进行分割的维度
        pivot = kd_node.dom_elt  # 进行分割的“轴”

        if target[s] <= pivot[s]:  # 如果目标点第s维小于分割轴的对应值(目标离左子树更近)
            nearer_node = kd_node.left  # 下一个访问节点为左子树根节点
            further_node = kd_node.right  # 同时记录下右子树
        else:  # 目标离右子树更近
            nearer_node = kd_node.right  # 下一个访问节点为右子树根节点
            further_node = kd_node.left

        temp1 = travel(nearer_node, target, max_dist)  # 递归遍历找到包含目标点的区域

        nearest = temp1.nearest_point  # 以此叶结点作为“当前最近点”
        dist = temp1.nearest_dist  # 更新最近距离

        nodes_visited += temp1.nodes_visited

        if dist < max_dist:
            max_dist = dist  # 最近点将在以目标点为球心，max_dist为半径的超球体内

        temp_dist = abs(pivot[s] - target[s])  # 第s维上目标点与分割超平面的距离
        if max_dist < temp_dist:  # 判断超球体是否与超平面相交
            return result(nearest, dist, nodes_visited)  # 不相交则可以直接返回，不用继续判断

        #----------------------------------------------------------------------
        # 计算目标点与分割点的欧氏距离
        temp_dist = sqrt(sum((p1 - p2)**2 for p1, p2 in zip(pivot, target)))

        if temp_dist < dist:  # 如果“更近”
            nearest = pivot  # 更新最近点
            dist = temp_dist  # 更新最近距离
            max_dist = dist  # 更新超球体半径

        # 检查另一个子结点对应的区域是否有更近的点
        temp2 = travel(further_node, target, max_dist)

        nodes_visited += temp2.nodes_visited
        if temp2.nearest_dist < dist:  # 如果另一个子结点内存在更近距离
            nearest = temp2.nearest_point  # 更新最近点
            dist = temp2.nearest_dist  # 更新最近距离

        return result(nearest, dist, nodes_visited)

    return travel(tree.root, point, float("inf"))  # 从根节点开始递归

‍ 测试一下上述代码：

ret = find_nearest(kd, [3,4.5])
print (ret)

References

• 《统计学习方法 - 第 2 版》
• 《Machine Learning in Action》
• 《机器学习 - 周志华》
• 黄海广 — 《统计学习方法》的代码实现
• Github - AiLearning
• 【Python】get()函数作用
• np.tile()函数的作用