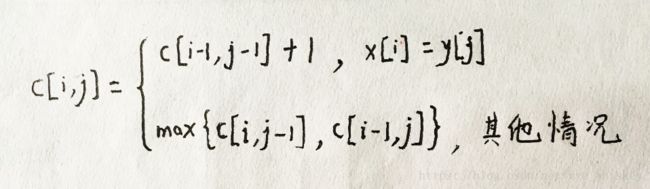MIT算法导论公开课之第15课 动态规划、最长公共子序列
动态规划(Dynamic programming)
动态规划是一种设计技巧,而不是一种特定的算法,就像分治法一样。
最长公共子序列(Longest common subsequence)问题
有两个序列,序列x[1~m],序列y[1~n],找到它们的最长公共子序列,子序列不需要在原序列中占用连续的位置(最长公共子串要求连续),子序列可能不唯一。
- Ex:
x:A B C B D A B
y:B D C A B A
公共子序列:BDAB BCAB BCBA(LCS(x,y))
暴力算法
检查x[1~m]的每个子序列在y[1~n]中也是否存在,找到其中最长的。
运行时间分析:
检查是否存在代价为O(n)
x中的子序列数量为2^m,可以用一个m位的向量来表示,1表示选取那个字符,0表示不选取那个字符。
总运行时间为O(n·2^m),指数级的运行时间是非常慢的。
LCS问题简化
1.计算最长公共子序列的长度(唯一)。
2.扩展算法使其能够找到最长公共子序列。
注:|S|表示序列S的长度。
动态规划策略
x[i]=y[j]的情况:
设z[1~k]=LCS(x[1~i],y[1~j]),且有c[i,j]=k,则有z[k]=x[i](=y[j])。
证明z[1~k-1]=LCS(x[1~i-1],y[1~j-1]):
假设存在w为x[1~i-1],y[1~j-1]的一个子序列且|w|>k-1。
w和z[k]合成的序列(剪贴法),也应是x[1~i],y[1~j]的一个子序列。
|w和z[k]合成的序列|>k。
与c[i,j]=k矛盾,假设不成立,z[1~k]=LCS(x[1~i],y[1~j])得证。
因此有c[i-1,j-1]=k-1,c[i,j]= c[i-1,j-1]+1。
x[i]≠y[j]的情况:
可利用与上面方法类似的方法证明。动态规划问题特性1
- 最优子结构,问题的最优解包含了子问题的最优解。
在最长公共子序列问题中,如果有z=LCS(x,y),那么z的某个前缀= LCS(x的某个前缀,y的某个前缀)。
LCS的递归算法伪码
LCS(x,y,i,j)//忽略基本情况
if x[i]=y[j]
c[i,j] ← LCS(x,y,i-1,j-1)+1
else
c[i,j] ← max{LCS(x,y,i-1,j), LCS(x,y,i,j-1)}
return c[i,j]动态规划问题特性2
- 重叠子问题,一个递归的过程包含一些数量的独立的子问题被重复计算了多次。
在最长公共子序列问题中,可以发现在递归树中有很多相同的子问题,可分析得独立子问题得数量为m·n。
LCS的备忘录递归算法伪码
LCS(x,y,i,j) //忽略基本情况
if c[i,j]=nil
if x[i]=y[j]
c[i,j] ← LCS(x,y,i-1,j-1)+1
else
c[i,j] ← max{LCS(x,y,i-1,j), LCS(x,y,i,j-1)}
return c[i,j]- 上述算法的运行分析:
运行时间为Θ(m·n),可从平摊代价的方面考虑,每次操作只有访问c[i,j]需要计算代价,递归操作会开启新的操作,重新计算平摊代价,所以运行时间为Θ(m·n)。
占用空间为Θ(m·n),占用空间较多,且计算c[i,j]表的过程比较混乱。
完善的动态规划算法
自底向上的计算c[i,j]表。
Ex:
x:A B C B D A B
y:B D C A B A
右下角即为最长公共子序列的长度,运行时间为Θ(m·n),且利用了内存访问的局部性特点,此算法效率很高。回溯法重建LCS:
BCBA即为一个最长公共子序列,走别的路径即可得到其他几个结果。
朴素算法占用空间为Θ(m·n),改进算法只使用两行或两列可将占用空间减小到O(min{m,n})。
思考:改进算法如何重建LCS?(提示:采用分治法)