SIGMOD论文研读—Overlap Set Similarity Joins with Theoretical Guarantees
前言:SIGMOD上一篇有关集合相似性的算法论文,本文仅是笔者对于论文的解读,欢迎读者来和笔者探讨、指出笔者的错误
论文标题:Overlap Set Similarity Joins with Theoretical Guarantees
作者:Dong Deng,Yufei Tao,Guoliang Li
刊物:SIGMOD
时间:June , 2018
出处链接:https://dl.acm.org/doi/abs/10.1145/3183713.3183748
文章目录
- 1.论文摘要
- 2问题定义
-
- 2.2.1 形式化定义
- 2.2.2 自然语言解释
- 2.2.3 举例说明
- 3算法或证明过程
-
- 3.1主要思想:
- 3.2伪代码表述算法整体框架:
- 3.3小集合处理方法的优化(针对伪代码中④部分)
- 3.3.1 HeapSkip:跳过只有单一集合的L[r]
- 3.3.2 HeapDedup:跳过只有一个集合的L[r]和冗余的L[r]
- 3.3.3BlockDedup
- 3.4边界x的选取
- 3.4.1 x的理论值:
- 3.4.2实际应用时x的取值
- 3.5实验结论
- 4.相关领域综述
-
- 4.1问题定义
- 4.2解决方法
- 4.2.1ScanCount:
- 4.2.2基于堆的Merge-skip
- 4.2.3Partition-Based Method:基于划分的方法
1.论文摘要
该论文研究了具有重叠约束的集合相似性连接问题,给定集合的两个集合和一个常数c,可以在数据集中找到至少共享c个共同元素的所有集合对。所有现有方法的时间复杂度为O(n^2),其中集合总数为n。该论文提出了一种尺寸感知算法,其时间复杂度为,其中k为最终的结果数。尺寸感知算法根据它们的大小将它们分为大集合和小集合,并分别处理它们。根据该论文的算法思想,我们可以使用任何一个现有的方法来处理大型集,因此该论文专注于小型集,为小集合开发了几种优化启发式算法,以显著提高实用性能。由于小集和大集之间的大小边界对效率至关重要,因此,论文还提出了一种有效的大小边界选择算法,以明智地选择合适的大小边界,表现更好的性能。
2问题定义
2.2.1 形式化定义
输入:两个集合R,S,以及常量c。其中R和S的元素均为集合
输出:{
2.2.2 自然语言解释
给定两个集合R,S,二者的元素均为集合,并给定常量c。
这里的常量c人为定义了集合相似的标准:只有当集合R1,S1的交集大小|R1∩S1|≥c时认为两个集合相似。
问题是要在R x S空间找到所有相似集合对
2.2.3 举例说明
R={R1,R2,R3},R1={e1,e2},R2={e1,e3,e4,e6},R3={e2,e5,e7}S={S1,S2},S1={e2,e5,e6},S2={e1,e2,e4,e5,e6,e7,e8}
给定常量c=2
则仅当两个集合R’,S’交集大小|R1∩S1|≥2时认为R’和S’相似
R x S={
按照论文本身的逻辑,先来解决一个集合自相似的问题,即对于2.2.1和2.2.2中定义,取R=S情况:给定集合R,R的元素均为集合,给定常量c。在R x R空间找到所有相似集合对
3算法或证明过程
注:为了叙述的简洁,以下叙述中使用“c-子集”来代替“大小为c的子集”这一叙述
n是所有集合中所有元素的总个数,k是最终结果中集合对的总个数
3.1主要思想:
-
分而治之,将所有集合元素进行划分:根据它们的大小划分为大集合Rl和小集合Rs,选定边界x,大集合是大小≥x的集合,小集合是大小
-
对于Rl x R,采用现有方法的任意一种进行处理均可,为了方便起见,这里选择简单的暴力搜索,遍历大集合中每一个元素Ri,再遍历R中每一个集合,直接作|Ri∩R|,看大小是否≥c
-
对于Rs x Rs,为每个c-子集r建立倒排索引L[r],保存有哪些元素包含了该子集r。由此,每个L[r]中的不同集合间都至少包含了r这个c-子集,满足条件,从而L[r]中不同集合间组成集合对,满足条件
3.2伪代码表述算法整体框架:
Input:集合R={R1,R2,···,Rm},指定常量c
Output:A={
①x=GetSizeBoundary(R,c) //确定大集合与小集合之间的划分标准
②依据x将R的元素划分为大集合Rl和小集合Rs,初始化A=¢
③for each 大集合Ri∈ Rl do
for each Rj∈ R do
If|Ri∩Rj|≥c
将<Ri,Rj>插入A中 //对于大集合直接暴力搜索
④for each 小集合Rj∈ Rs do
for each Rj的大小为c的子集r do
将Rj插入到L[r]中 //小集合对c-子集建立倒排索引
⑤for each L[r] do
将L[r]中不同集合组成集合对加入A中
⑥return A正确性证明:
①显然,算法囊括了Rl x R空间的所有元素
②对于Rs x Rs部分,只要有两个集合R1,R2满足相似条件,它们交集的大小≥c,取该交集的一个子集r,r的大小为c,则必有R1,R2均在L[r]中;而若L[r]中有两个集合R1,R2,则说明R1,R2的交集有一个c-子集r,因此|R1∩R2|≥c。故由论证可值Rs x Rs部分的算法是充要的,一定可以找到小集合中的所有满足条件集合对。
③由主要思想的论述可知,我们无需再判断Rs x Rl部分的元素,Rl x R和Rs x Rs已经囊括了解空间,因此一定可以生成所有的解。
这是一个整体框架,还有两个地方需要填充进框架中来:
1)小集合处理方法的优化 2)划分边界x的确定
3.3小集合处理方法的优化(针对伪代码中④部分)
3.3.1 HeapSkip:跳过只有单一集合的L[r]
由于这种优化的功能被3.3.2所囊括,且方法3.3.2可进行更多优化,因此这里只作简单介绍。
我们为每一个小集合的元素都进行全局标号,对c-子集排序,具体可见(2)。并建立(2)中所述的最小堆。这样一来,每次通过堆顶得到一个当前最小的c-子集r,假定r来自小集合R,设r2是剔除r之后的堆顶元素,则r2可表示Rs\R的集合中最小的c-子集,来自R2,可见图示:

这里用左右的位置关系来表示定义的集合“大小关系”,则R中的c-子集r’满足: r
3.3.2 HeapDedup:跳过只有一个集合的L[r]和冗余的L[r]
Input: Rs:所有小集合的集合 ;c:常量,集合相似的判断标准
Output:精简的倒排索引L
①对Rs中所有小集合中的所有元素e进行全局标号(标号规则任意选取,如随机生成下标),标号小,则认为该元素“更小”,同时利用这种标号新定义集合间的“大小关系”:对集合R1,R2,若R1中“最小”(标号)的元素比R2中“最小”的元素“更小”,则R1小于R2,若相等,则比较“次小”元素···;据此,将每个小集合中的c-子集按照这种“大小关系”进行排序。
②对于每个小集合,将每个小集合的“最小”(依据标号)的c-子集拿出来建立一个最小堆H,入堆的同时记录每个子集来自哪一个小集合Ri。
③While H ≠ ¢
记min=H的堆顶元素,删除min。得到min的来源R,将R加入L[min]中。
top为删除min之后的堆顶元素
if top≠min then
for each Ri in L[min] do
对Ri进行二分搜索,找到Ri中第一个≥top的c-子集,插入H中
else
continue
④return L该优化方法的思想基于以下事实:
1) L[r1]⊆ L[r2],则r1是冗余的,因为L[r1]产生的集合对一定包含在L[r2]的集合对中
2) 对于r1和L[r1],设r2为Rs\L[r1]的集合中最小的c-子集,则满足:r1
②其次L[r]∩(Rs\L[r1])=¢.否则在Rs\L[r1]中存在集合R包含集合r,由①可知,R应在L[r1]中,矛盾。从而L[r]⊆ L[r1],r是冗余的
有了上面的事实依据,算法便很好理解。
1)每次循环时若min=top,直接continue实现lazy处理,从而下次选取时将top所在集合R’加入L[min]中
2)每次循环时若min≠top,由于top是当前最小c-子集,只有两种可能:
①top为Rs\L[min]的最小c-子集。则由上面的分析,所有位于min和top之间的c-子集都是冗余的,可以跳过
②top为L[min]的最小c-子集(除min之外),设r为Rs\L[min]的最小c-子集,则有r≥top。故位于min和r之间的所有c-子集都是冗余的,但由于r未知,我们转而利用top,因为top≤r,必有min和top之间的c-子集都是冗余的。
无论如何,min和top之间的c-子集均是冗余的,从而我们对于L[min]中的每个集合都利用二分搜索找到第一个≥top的c-子集,插入到堆H中,将那些冗余子集跳过。同时由于min=top时的lazy处理,我们在min≠top时的处理是针对L[min]中一组集合的操作,包含了Heapskip的功能。
3.3.3BlockDedup
对3.3.2继续进行优化:3.3.2中的堆保存着每个小集合的最小c-子集,因此堆的大小是|Rs|,这里的思想是分别多次建立更小的堆来降低堆的操作的复杂度。
我们用B[e]来表示所有满足这样条件的集合:集合中“最小”的元素是e。(这里的“小”是根据前述定义的“标号”),可以对于每个B[e]分别建堆,调用3.3.2中的方法得到一个L,将每次得到的结果并在一起(集合的并),则保证了遍历所有集合,同时又减少了堆的大小,从而改善性能。
我们可以很容易地为每一个元素e建立倒排索引I[e],使其保存所有包含e的集合。由B[e]的定义可知,B[e]是I[e]的一个子集,然后我们将I[e]的所有集合中所有小于e的元素移除,这样剩余的就是B[e]与一些非B[e]集合(这里统称为T)的子集,但这些子集也可当作B[e]中集合,因为如果这些子集和那些B[e]中集合满足相似条件,那么T肯定也可以满足条件。另外我们也可以将元素e移除,因为这些集合都包含元素e,可以移除e,然后调用3.3.2中方法时传入常量c-1,这样判断时可以免去对元素e的重复判断。
可以用伪代码简单表示一下:
①为Rs中集合的所有元素建立倒排索引I, L初始化为空
②for each I[e] in I do
Rtmp=移除所有≤e的元素后的集合I[e]
L=L∪HeapDedup(Rtmp,c-1)
③return L3.4边界x的选取
3.4.1 x的理论值:
把时间复杂度表示为x的函数,选取x使复杂度最小。令k=最终结果中集合对的个数。
①为所有大集合建立哈希表,从而可在常数时间判断元素e是否属于该集合,由于大集合的大小≥x,故大集合个数至多为n/x,因此算法中对于一个大集合R1,计算交集|R1∩R’|的时间是O(|R’|),从而大集合的复杂度为O(|R’|*n/x)=O(n^2/x).
②而对于小集合部分,每个小集合|R1|≤x,含有![]() 个c-子集,从而枚举c-子集占用时间
个c-子集,从而枚举c-子集占用时间![]() ≤
≤![]() ≤x^(c-1)
≤x^(c-1)![]() ≤ nx^c-1 ,上界为O(n x^c-1)
≤ nx^c-1 ,上界为O(n x^c-1)
假设生成了t个倒排索引,则所有倒排索引大小之和与枚举的c-子集个数一致,故 =
=![]() ,而对于每个倒排索引,我们遍历的时候还要将其中的集合两两组合成对,因此占用时间
,而对于每个倒排索引,我们遍历的时候还要将其中的集合两两组合成对,因此占用时间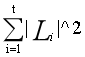 。而对于每个Li,生成的结果对数为(|Li||Li-1|)/2≤k(因为k是总结果对数,一个倒排索引生成的结果数必然小于等于k),则|Li|=O(k^(1/2)),故时间上界为
。而对于每个Li,生成的结果对数为(|Li||Li-1|)/2≤k(因为k是总结果对数,一个倒排索引生成的结果数必然小于等于k),则|Li|=O(k^(1/2)),故时间上界为![]() 因此整个算法总复杂度为
因此整个算法总复杂度为![]()
③若k已知,令函数取最小值,可得x=![]()
④但k往往是未知的,使用“doubling Trick”,用k’猜测k,从k’=1开始尝试,如果正确,则应该执行的步骤个数为![]() ,其中α为②中总复杂度隐含的常量,一旦执行的步骤个数为
,其中α为②中总复杂度隐含的常量,一旦执行的步骤个数为![]() 时,我们知道k’<k,然后将其加倍,重复操作直到k’≥k,每一轮的时间为
时,我们知道k’<k,然后将其加倍,重复操作直到k’≥k,每一轮的时间为![]()
从而时间上界仍为 故仍可采用k已知时的x取值
故仍可采用k已知时的x取值
3.4.2实际应用时x的取值
由于我们对小集合部分的优化加之理论分析的是时间的“上界”,故可能理论取值效果并不理想。实际选取时可令x从某一值开始不断加1进行尝试,每一次估计以其值运行算法的时间,当时间开始增加时终止,以该值作为最终的x值。初始取值:令t=R中最小集合的大小,x=max{t,c}
①对于大集合,实际应用时这里选择ScanCount方法,像BlockDedup方法一样为每个元素e建立倒排索引,代价正比于![]()
(注:ScanCount![]() )
)
故估算大集合代价:![]()
②对于小集合,生成倒排索引的代价取决于堆操作以及二分搜索,随机取z个BlockDedup中提及的B[e],估算它们的代价Cost,而B[e]的总个数为Z=|I|,故估算生成倒排索引代价为Cost*Z/z。
对于倒排索引生成集合对的代价:如果两个集合间有p个公共元素,则它们有![]() 个公共c-子集,从而它们会被生成
个公共c-子集,从而它们会被生成![]() 次。故生成集合对的代价可根据集合间公共元素的个数估算。随机取y个集合对,第i个集合对间共享元素个数为pi,我们一共有Y=
次。故生成集合对的代价可根据集合间公共元素的个数估算。随机取y个集合对,第i个集合对间共享元素个数为pi,我们一共有Y=![]() 个集合对,故估算代价为
个集合对,故估算代价为![]()
3.5实验结论
针对具有重叠约束的集合相似性连接问题,该论文提出了一种具有时间复杂度的尺寸感知算法,其中,n是所有集合的总数,k是最终结果的数量。论文将所有集合分为小集合和大集合,并分别进行处理。对于小型集合,我们枚举其所有c-子集,并取任何共享至少一个c-子集的集合对。为了避免枚举不必要的c子集,论文描述了一种基于堆的方法来避免无法生成任何结果的唯一c子集和仅生成重复结果的冗余c子集。同时,论文还提出一种阻塞c子集的方法以减少堆大小和堆调整成本。并且还设计了一种有效的方法来选择合适的尺寸边界。
4.相关领域综述
相关问题:编辑距离约束下的字符串相似连接
4.1问题定义
输入:两个字符串集合R,S,编辑距离下界常量c
输出:所有编辑距离不超过c的字符串对A={(r,s)|r与s的编辑距离≤c,r∈R,s∈S}
相关定义:字符串s的长度表示为|s|,每个字符串s对应一个id进行标识,ed(r,s)表示r与s的编辑距离,q-gram是一个长度为q的连续子串,其所在字符串中起始位置被称为q-gram的位置.简单来说是这样的:假如有字符串acfj,做一个q=2的q-gram切分,则生成集合{ac,cf,fj},把字符串按照顺序切分成长度为q的子串。对于每一个gram w都可以建立一个链表I,其中的元素形式为(id,loc),id标识w所在字符串s,loc标识w在串s中的位置。
4.2解决方法
4.2.1ScanCount:
利用q-gram找到一个ed(r,s)的必要条件:若ed(r,s)≤c,则r和s至少包含T=(max{|r|,|s|}-q+1)-qc个公共的q-gram。这是因为max{|r|,|s|}-q+1是二者中长度更长的串的q-gram,c个编辑操作至多影响cq个q-gram,因此公共的q-gram至少为(max{|r|,|s|}-q+1)-q*c个。
于是我们为字符串集合中的所有字符串的q-gram建立倒排表,倒排表中的每一个元素是一个二元组
然后我们可以遍历R中每个字符串r的链表,对于每个链表,记录S中每个字符串s的出现次数,如果某字符串s出现次数≥T,说明满足上述条件,将(r,s)作为备选对加入到输出集A中。
故我们需要一个数组B[|S|]来记录S中每个字符串的出现次数,初始化为0.
然后我们遍历R中的所有字符串r,对于r的每一个q-gram,遍历它的链表Ir。假设遍历到链表中的某一个id标识了字符串s∈S,则B[id]+1。每当遍历完一个链表以后,将B中值≥T对应的字符串与r构成字符串对(r,s)加入A中,然后可将B重新初始化以供下一个R中字符串的链表的遍历。
遍历完成后,我们的输出集A中包含的所有集合对(r,s),都至少包含T=(max{|r|,|s|}-q+1)-q*c个公共的q-gram。但这只是必要条件,因此我们对于每一对(r,s),计算二者的编辑距离,将真正满足条件的保留下来,形成最后的输出集A
4.2.2基于堆的Merge-skip
仍然是利用4.2.1中提到到q-gram以及其倒排表,4.2.1中已经提到,每个倒排表都是升序有序的,因此我们对于R中的每一个串,为该串包含的所有q-gram倒排表建立最小堆:将其中id最小的元素取出来建堆H,如图中的例子所示,图中的数字均表示id:
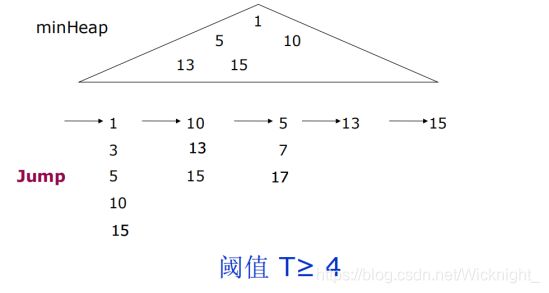
然后当H不空时,我们执行如下操作:
1)取堆顶元素p=
2)若N>=T(T的定义见上文ScanCount),说明该串与该id代表的串有超过T个公共q-gram,组成备选对加入集合中,并从对应链表中选取下一个最小元素加入堆中。
3)若N 然后,取新堆顶p’,并且对于剔除出去的那些元素所属的链表,利用二分搜索,找到第一个id大于等于id_p’的元素,加入堆中,从而跳过了很多元素。而这些元素是肯定不符合条件的,因为这些元素的id都小于id_p’,和刚才分析的剔除元素道理一样。 4)重复1),2),3)过程直到堆为空。 基于这样一种方法,在3)和4)中实现了对更多必然不满足条件的串的跳过,实现了进一步优化。 划分是什么?我们这里使用一种平均划分,简单说来,如果s为任意一个待划分的字符串,将s划分为α+1部分,令k=|s|%(α+1),则我们可以推得前α+1-k部分中每一部分都含有⌊|s|/(α+1)⌋个字符,最后k部分均包含⌈|s|/(α+1)⌉个字符,这样保证了不会出现前面的部分占用很多字符,而后面的字符出现单挂一个、两个字符的情况,保证了相对的平均。 那么如何将划分思想运用到字符串相似上呢?对于两个字符串r,s,如果它们两个相似(编辑距离不超过c),则将s(或r)进行c+1划分,则要求r(或s)中至少包含s(或r)的c+1划分中的其中一个。否则的话,r不包含任意一个划分,则每个划分至少s和r至少有一个不同点,这样c+1个划分就会产生至少c+1个不同点,从而编辑距离至少为c+1,矛盾。这样我们便得到一个必要条件,利用该条件剔除一些字符串,免去繁多的编辑距离计算,产生一些候选对。这时只需要再对候选对进行编辑距离计算进行验证即可。具体步骤可以这样简要概括: 1)首先将所有字符串按长度由小到大排序,相同长度的长度按字典序 2)由小到大遍历集合S中所有字符串s,将s进行c+1划分,建立并维护倒排索引 3)在遍历S中所有字符串s的过程中,同时产生候选对:遍历所有的 注意,这里的长度选择为|s|-c≤|r|≤|s|,是因为长度≤|s|-c-1的字符串长度与|s|已经相差至少c+1,编辑距离至少为c+1,因此可以排除。而不选择大于|s|的原因是按升序遍历时,大于|s|的部分还没有建立索引,同时,这种候选对会在遍历到大于|s|的字符串时遍历到,如果此时先遍历,也会造成重复。因此没有必要。4.2.3Partition-Based Method:基于划分的方法
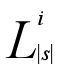 ,其中保存所有长度为|s|的字符串的第i个划分。
,其中保存所有长度为|s|的字符串的第i个划分。
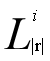 (其中|s|-c≤|r|≤|s|,1≤i≤c+1),即长度处于|s|-c≤|r|≤|s|之间的所有倒排索引,检查s的子串,如果s有某个子串t是某个
(其中|s|-c≤|r|≤|s|,1≤i≤c+1),即长度处于|s|-c≤|r|≤|s|之间的所有倒排索引,检查s的子串,如果s有某个子串t是某个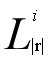 中的划分,则说明s和包含该划分的所有字符串(在
中的划分,则说明s和包含该划分的所有字符串(在 (t)中保存)是候选对,验证他们的编辑距离,如果真的满足条件,加入到输出集合中。这样遍历完成时输出集合也已经确定。
(t)中保存)是候选对,验证他们的编辑距离,如果真的满足条件,加入到输出集合中。这样遍历完成时输出集合也已经确定。