【图像处理】 仿射变换(Affine Transformation)和透视变换(Perspective Transformation)
【图像处理】 仿射变换(Affine Transformation)和透视变换(Perspective Transformation)
- 齐次坐标系
- 仿射变换的原理
- OpenCV中的仿射变换
- 仿射变换的部分应用
- 透视变换的原理
- OpenCV中的透视变换及应用
- 结语
齐次坐标系
欧式空间中,使用用笛卡尔坐标系,对应的,在透视空间中,使用齐次坐标系。
齐次坐标用 n + 1 n+1 n+1维,对应表示笛卡尔坐标的 n n n维,比如:
笛卡尔坐标中的 ( x , y ) (x, y) (x,y)对应齐次坐标中的 ( x 1 , y 1 , w ) (x_1,y_1,w) (x1,y1,w),有 x = x 1 w x=\dfrac{x_1}{w} x=wx1, y = y 1 w y=\dfrac{y_1}{w} y=wy1
笛卡尔坐标中的 ( 2 , 3 ) (2, 3) (2,3)对应齐次坐标中的 ( 2 , 3 , 1 ) (2,3,1) (2,3,1)等
特别的,笛卡尔坐标中的 ( + ∞ , + ∞ ) ( +\infty, +\infty) (+∞,+∞)对应齐次坐标中的 ( 2 , 3 , 0 ) (2,3,0) (2,3,0)等
仿射变换的原理
仿射变换,是一次空间线性变换,或多次不同空间线性变换的组合。经过仿射变换后,直线还是直线,圆弧还是圆弧,互为平行线还是互为平行线,但是,不能保证线段的长度和线段之间的夹角角度不变。
仿射变换的原始空间线性变换包括:
(下面四种仿射变换的原始空间线性变换的示意图来自https://www.cnblogs.com/happystudyeveryday/p/10547316.html,感谢原作者的工作)
-
平移变换(Translation Transformation)

用笛卡尔坐标系表示:
x ^ = x + t x \hat{x}=x+t_x x^=x+tx
y ^ = y + t y \hat{y}=y+t_y y^=y+ty
用齐次坐标系表示:
[ x ^ y ^ 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] ∗ [ x y 1 ] \begin{bmatrix}{\hat{x}}\\{\hat{y}}\\1\end{bmatrix} = \begin{bmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{bmatrix} * \begin{bmatrix}{x}\\{y}\\1\end{bmatrix} ⎣⎡x^y^1⎦⎤=⎣⎡100010txty1⎦⎤∗⎣⎡xy1⎦⎤ -
旋转变换(Rotation Transformation)
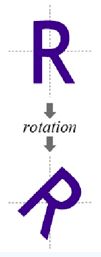
图形围绕原点顺时针旋转 θ \theta θ弧度
用笛卡尔坐标系表示:
x ^ = x c o s ( θ ) − y s i n ( θ ) \hat{x}=xcos(\theta)-ysin(\theta) x^=xcos(θ)−ysin(θ)
y ^ = x s i n ( θ ) + y c o s ( θ ) \hat{y}=xsin(\theta)+ycos(\theta) y^=xsin(θ)+ycos(θ)
用齐次坐标系表示:
[ x ^ y ^ 1 ] = [ c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) 0 0 0 1 ] ∗ [ x y 1 ] \begin{bmatrix}{\hat{x}}\\{\hat{y}}\\1\end{bmatrix} = \begin{bmatrix}cos(\theta)&-sin(\theta)&0\\sin(\theta)&cos(\theta)&0\\0&0&1\end{bmatrix} * \begin{bmatrix}{x}\\{y}\\1\end{bmatrix} ⎣⎡x^y^1⎦⎤=⎣⎡cos(θ)sin(θ)0−sin(θ)cos(θ)0001⎦⎤∗⎣⎡xy1⎦⎤ -
剪切变换(Shear Transformation )
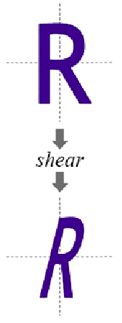
用笛卡尔坐标系表示:
x ^ = x + y ∗ t x \hat{x}=x + y*t_x x^=x+y∗tx
y ^ = y + x ∗ t y \hat{y}=y+x*t_y y^=y+x∗ty
用齐次坐标系表示:
[ x ^ y ^ 1 ] = [ 1 t x 0 t y 1 0 0 0 1 ] ∗ [ x y 1 ] \begin{bmatrix}{\hat{x}}\\{\hat{y}}\\1\end{bmatrix} = \begin{bmatrix}1&t_x&0\\t_y&1&0\\0&0&1\end{bmatrix} * \begin{bmatrix}{x}\\{y}\\1\end{bmatrix} ⎣⎡x^y^1⎦⎤=⎣⎡1ty0tx10001⎦⎤∗⎣⎡xy1⎦⎤ -
放缩变换(Scale Transformation)
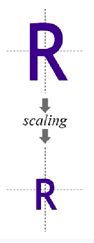
用笛卡尔坐标系表示:
x ^ = x ∗ t x \hat{x}=x*t_x x^=x∗tx
y ^ = y ∗ t y \hat{y}=y*t_y y^=y∗ty
用齐次坐标系表示:
[ x ^ y ^ 1 ] = [ t x 0 0 0 t y 0 0 0 1 ] ∗ [ x y 1 ] \begin{bmatrix}{\hat{x}}\\{\hat{y}}\\1\end{bmatrix} = \begin{bmatrix}t_x&0&0\\0&t_y&0\\0&0&1\end{bmatrix} * \begin{bmatrix}{x}\\{y}\\1\end{bmatrix} ⎣⎡x^y^1⎦⎤=⎣⎡tx000ty0001⎦⎤∗⎣⎡xy1⎦⎤
到这里就体现出齐次坐标系的作用了:通过使用齐次坐标系表示,将各种线性空间变换的表示都统一了
所以仿射变换可以表示为:
[ x ^ y ^ 1 ] = [ t x 0 0 0 t y 0 0 0 1 ] ∗ [ 1 t x 0 t y 1 0 0 0 1 ] ∗ [ c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) 0 0 0 1 ] ∗ [ 1 0 t x 0 1 t y 0 0 1 ] ∗ [ x y 1 ] \begin{bmatrix}{\hat{x}}\\{\hat{y}}\\1\end{bmatrix} = \begin{bmatrix}t_x&0&0\\0&t_y&0\\0&0&1\end{bmatrix} * \begin{bmatrix}1&t_x&0\\t_y&1&0\\0&0&1\end{bmatrix} * \begin{bmatrix}cos(\theta)&-sin(\theta)&0\\sin(\theta)&cos(\theta)&0\\0&0&1\end{bmatrix} *\begin{bmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{bmatrix} *\begin{bmatrix}{x}\\{y}\\1\end{bmatrix} ⎣⎡x^y^1⎦⎤=⎣⎡tx000ty0001⎦⎤∗⎣⎡1ty0tx10001⎦⎤∗⎣⎡cos(θ)sin(θ)0−sin(θ)cos(θ)0001⎦⎤∗⎣⎡100010txty1⎦⎤∗⎣⎡xy1⎦⎤
(注意上式中,不同变换矩阵中的 t x t_x tx、 t y t_y ty不相同)
[ x ^ y ^ 1 ] = [ a 1 a 2 a 3 a 4 a 5 a 6 0 0 1 ] ∗ [ x y 1 ] \begin{bmatrix}{\hat{x}}\\{\hat{y}}\\1\end{bmatrix} =\begin{bmatrix}a_1&a_2&a_3\\a_4&a_5&a_6\\0&0&1\end{bmatrix} *\begin{bmatrix}{x}\\{y}\\1\end{bmatrix} ⎣⎡x^y^1⎦⎤=⎣⎡a1a40a2a50a3a61⎦⎤∗⎣⎡xy1⎦⎤
故,仿射变换的变换矩阵有六个自由度,至少需要三对对应点求得。
OpenCV中的仿射变换
- 根据三个对应点,求得仿射变换矩阵
M = cv2.getAffineTransform(src, dst)
- M:仿射变换矩阵
- src:原始图像中的三个点的坐标
- dst:变换后得到图像中对应的三个点的坐标
- 根据仿射变换矩阵,将图像进行仿射变换
dst = cv2.warpAffine(src, M, dsize)
- dst:仿射变换后得到的图像
- src:原始图像
- M:仿射变换矩阵
- dsize:仿射变换得到图像的size(注意和resize操作的差别)
仿射变换的部分应用
# -*- coding:utf-8 -*-
import cv2
import numpy as np
img = cv2.imread("test_image.jpg")
cv2.circle(img, (185, 330), 3, (0, 0, 213), -1)
cv2.circle(img, (285, 135), 3, (0, 0, 213), -1)
cv2.imshow("input", img)
cv2.waitKey(0)
kp2 = np.array([285.0, 135.0])
kp0 = np.array([185.0, 330.0])
dir_v = kp2 - kp0
# 两个关键点之间的距离
dist = np.linalg.norm(dir_v)
dir_v /= np.linalg.norm(dir_v)
R90 = np.r_[[[0, 1], [-1, 0]]]
dir_v_r = dir_v @ R90.T
a = np.float32([kp2, kp2 + dir_v*dist, kp2 + dir_v_r*dist])
b = np.float32([
[int(dist), int(dist)],
[int(dist), 0],
[0, int(dist)]])
Mtr = cv2.getAffineTransform(a, b)
img_ = cv2.warpAffine(img, Mtr, (500, 500))
cv2.imshow("output", img_)
cv2.waitKey(0)
透视变换的原理
透视变换,又叫单应性变换。
简而言之就是不同视角的同一物体,在像素坐标系中的变换。
对于齐次坐标系,有:
[ x ^ y ^ 1 ] = [ h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h 9 ] ∗ [ x y 1 ] \begin{bmatrix}{\hat{x}}\\{\hat{y}}\\1\end{bmatrix} =\begin{bmatrix}h_1&h_2&h_3\\h_4&h_5&h_6\\h_7&h_8&h_9\end{bmatrix} *\begin{bmatrix}{x}\\{y}\\1\end{bmatrix} ⎣⎡x^y^1⎦⎤=⎣⎡h1h4h7h2h5h8h3h6h9⎦⎤∗⎣⎡xy1⎦⎤
即:
x ^ = h 1 ∗ x + h 2 ∗ y + h 3 \hat{x}=h_1*x+h_2*y+h_3 x^=h1∗x+h2∗y+h3
y ^ = h 4 ∗ x + h 5 ∗ y + h 6 \hat{y}=h_4*x+h_5*y+h_6 y^=h4∗x+h5∗y+h6
1 = h 7 ∗ x + h 8 ∗ y + h 9 1=h_7*x+h_8*y+h_9 1=h7∗x+h8∗y+h9
即:
x ^ = h 1 ∗ x + h 2 ∗ y + h 3 h 7 ∗ x + h 8 ∗ y + h 9 \hat{x}=\dfrac{h_1*x+h_2*y+h_3}{h_7*x+h_8*y+h_9} x^=h7∗x+h8∗y+h9h1∗x+h2∗y+h3
y ^ = h 4 ∗ x + h 5 ∗ y + h 6 h 7 ∗ x + h 8 ∗ y + h 9 \hat{y}=\dfrac{h_4*x+h_5*y+h_6}{h_7*x+h_8*y+h_9} y^=h7∗x+h8∗y+h9h4∗x+h5∗y+h6
齐次坐标系有性质:
( x ^ , y ^ , 1 ) = ( x ^ h 9 , y h 9 , 1 h 9 ) (\hat{x},\hat{y},1)=(\dfrac{\hat{x}}{h_9}, \dfrac{y}{h_9},\dfrac{1}{h_9}) (x^,y^,1)=(h9x^,h9y,h91)
因此,有:
x ^ = h 1 / ∗ x + h 2 / ∗ y + h 3 / h 7 / ∗ x + h 8 / ∗ y + 1 \hat{x}=\dfrac{ {h_1}^/*x+{h_2}^/*y+{h_3}^/}{ {h_7}^/*x+{h_8}^/*y+1} x^=h7/∗x+h8/∗y+1h1/∗x+h2/∗y+h3/
y ^ = h 4 / ∗ x + h 5 / ∗ y + h 6 / h 7 / ∗ x + h 8 / ∗ y + 1 \hat{y}=\dfrac{ {h_4}^/*x+{h_5}^/*y+{h_6}^/}{ {h_7}^/*x+{h_8}^/*y+1} y^=h7/∗x+h8/∗y+1h4/∗x+h5/∗y+h6/
故,透视变换的变换矩阵有八个自由度,至少需要四对对应点求得。
OpenCV中的透视变换及应用
# -*- coding:utf-8 -*-
import cv2
import numpy as np
import sys
template_img = cv2.imread("template.jpg")
template_img_gray = cv2.imread("template.jpg", 0)
img = cv2.imread("image.jpg")
img_gray = cv2.imread("image.jpg", 0)
sift = cv2.xfeatures2d.SIFT_create()
# sift算子提取特征
tem_key_points, tem_descriptors = sift.detectAndCompute(template_img_gray, None)
img_key_points, img_descriptors = sift.detectAndCompute(img_gray, None)
# 特征匹配
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(tem_descriptors, img_descriptors, k=2)
# 去除最好匹配数量不是2的特征匹配
temporary = []
for each in matches:
if len(each) != 2:
temporary.append(each)
for each in temporary:
matches.remove(each)
good_match = []
for i, (m, n) in enumerate(matches):
if m.distance < 0.9 * n.distance:
good_match.append(m)
MIN_MATCH_COUNT = 4
if len(good_match) > MIN_MATCH_COUNT:
src_pts = np.float32([tem_key_points[m.queryIdx].pt for m in good_match]).reshape(-1, 1, 2)
dst_pts = np.float32([img_key_points[m.trainIdx].pt for m in good_match]).reshape(-1, 1, 2)
# 计算单应性矩阵
M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 3.0)
match_mask = mask.ravel().tolist()
draw_params = dict(matchColor=(0, 255, 0), singlePointColor=None, matchesMask=match_mask, flags=2)
match_image = cv2.drawMatches(template_img_gray, tem_key_points, img_gray, img_key_points, good_match, None, **draw_params)
cv2.imshow("Match Image", match_image)
while True:
if cv2.waitKey(1000 // 12) & 0xff == ord("q"): # 按q退出
break
cv2.destroyAllWindows()
if M is not None:
h, w, _ = template_img.shape
pts = np.float32([[0, 0], [0, h - 1], [w - 1, h - 1], [w - 1, 0]]).reshape(-1, 1, 2)
rect = cv2.perspectiveTransform(pts, M)
rect_ = []
for each in rect.tolist():
rect_.append([int(each[0][0]), int(each[0][1])])
box_image = cv2.polylines(img, [np.array(rect_)], True, (255, 0, 255), 3, cv2.LINE_AA)
cv2.imshow("Box Image", box_image)
while True:
if cv2.waitKey(1000 // 12) & 0xff == ord("q"): # 按q退出
break
cv2.destroyAllWindows()
else:
sys.exit(0)
else:
sys.exit(0)
测试图片
匹配图
通过单应性矩阵得到的检测框
结语
如果您有修改意见或问题,欢迎留言或者通过邮箱和我联系。
手打很辛苦,如果我的文章对您有帮助,转载请注明出处。


