斯坦福 算法1 第三周作业

来自斯坦福网站的Algorithms: Design and Analysis，与目前coursera上的版本内容没有变化，不过时间安排略有不同。

1 Problem Set 3

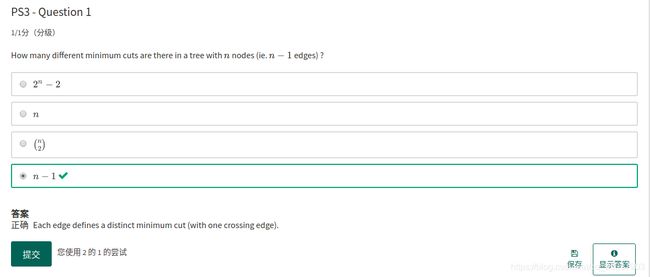
作为树的图最小割的个数。这是最小割的交叉边是1，对应每条边都是一个交叉边，也就是对应一个最小割。

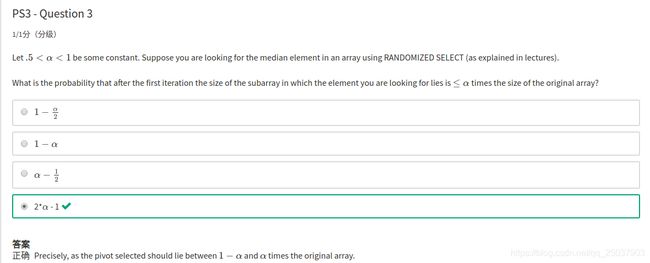
当图对应是一个环时，前三个都满足，概率就是p，也就对应着最大数量的最小割。但是并非所有的图都存在这样的最小割，根据推导，一般情况都是大于等于p。

显然。

每次留下$\alpha$n的数量，直到1为止。

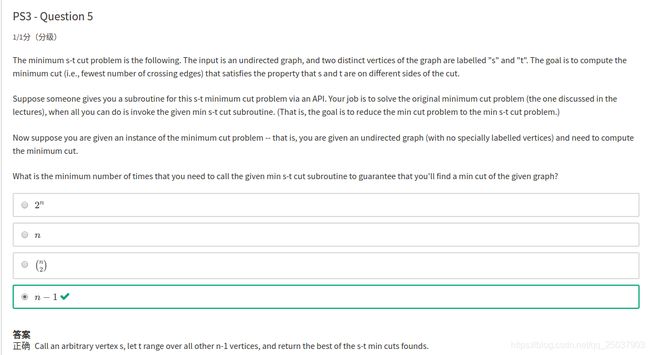
固定一个点，遍历对应n-1的组合。在这n-1个组合里比如有至少一个是两个点分别在A和B中。

2 Optional Theory Problems

1 一脸懵逼。看了这个链接里的解释大概懂了吧。ppt中已经证明了某个确定性的算法的复杂度是$\Omega (nlogn)$，要做的就是将随机性算法转化为确定性的概率和。假设某个随机性算法中的一种运行情况对应随机事件s，概率为$Pr(s)$。而这种运行情况相当于一个确定性算法，因此随机算法的复杂度为${\sum }_{s}Pr(s)\Omega (nlogn)=\Omega (nlogn)$，因此得证。具体可以看链接中的解释。
2 7是可以的，但3不可以。主要区别在于如下过程中证明的部分：

这里如果改为7，那么对应的两个数字就是n/7与5n/7，依然可以成立。然而对应3的n/3与2n/3不能让不等式成立。

3 用$O(n)$的方法计算权重中位数。想了半天以为是转化为linear selection，没想出来。没想到是直接类似linear selection做个新算法。伪代码如下：

思路如下：1. 先找到x数组的中位数x[k]。2. 计算小于x[k]的x对应的系数w之和。如果大于一半则保留下小于x[k]的x与对应的w，递归计算。否则保留大于x[k]的部分。

4 感觉依然是多项式表示的，不过最多是n个。写了个证明不知道是否正确：

• 有向图中最小割的交叉边数量依然为k。而每个边的出度大于等于k。因此$nk\le m$
• Pr(第i步选不到交叉边|第i-1步选不到交叉边) = $\frac{n-i}{n}$
• 因此Pr(结果是最小割）=$\frac{1}{n}$

因此有向图中最小割个数最多是n个。证明过程有些简陋，对照ppt看吧。

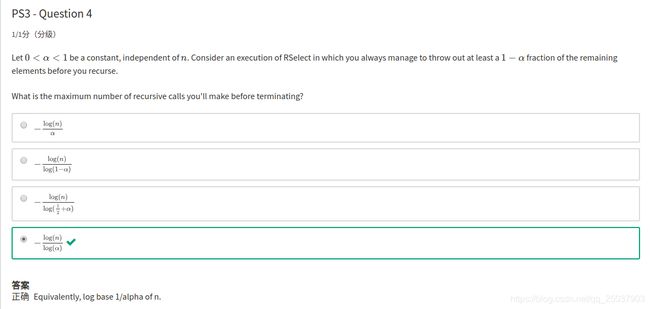
5 这只要在证明的时候每个概率的地方加上$\alpha$，最后结果$Pr(一次算法结果是\alpha -minimum-cut)=\frac{2{\alpha }^{n-2}}{n(n-1)}$，于是上限就是这个概率的倒数。

3 Programming Assignment 3

实现一个压缩最小割算法。很蛋疼，debug了很久。

实现如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

unordered_map> readGraph(string fileName) {
    cout << "read data from "<< fileName <> linkedLists;
    int tmp;
    int v;
    if(input) {
        while(getline(input,line)) {
            vector dl;
            istringstream ist(line);
            ist >> v;
            while(ist >> tmp)
                dl.push_back(tmp);
            linkedLists[v] = dl;
        }
    }
    return linkedLists;
}

int contraction_one(unordered_map> graph, vector edges) {
    int index;
    while(graph.size() > 2) {
        index = rand()%edges.size();//选一个边
        int rem = edges[index]/1000, del = edges[index]%1000;//将节点del合并到rem

        if(graph.find(rem) == graph.end() || graph.find(del) == graph.end()) {
            cout << "wrong"<>& graph, vector& edges) {
    cout << "contraction start..."<> graph;
    graph = readGraph("kargerMinCut.txt");
    vector edges;
    for(auto& k : graph)
        for(int x : k.second)
            edges.push_back(k.first*1000+x);
    contraction(graph,edges);
    return 0;
}

用了两个结构表示图，一个是邻接表，一个是边的vector。每个边用一个整数表示，1000×a+b。由于是无向图，每个边都有(a,b)和(b,a)两个，很容易代码就会漏掉。核心部分都有注释，应该看得懂。

4 彩蛋：Linear Selection 实现

用了随机性选择的算法，正好是leetcode 215题，实现方式是三路partition（考虑重复元素），AC代码如下：

class Solution {
public:
    int findKthLargest(vector& nums, int k) {
        return helper(nums,0,nums.size(),k);
    }
    
    int helper(vector& nums, int begin, int end, int k) {
        if(k == 1 && begin+1 == end) return nums[begin];
        int pivot = nums[begin];
        int left = begin+1, mid = left, right = mid;
        while(right < end) {
            if(nums[right] == pivot) {
                swap(nums[right],nums[mid]);
                mid++;
            }else if(nums[right] > pivot) {
                swap(nums[right],nums[left]);
                if(mid > left)
                    swap(nums[right],nums[mid]);
                left++;
                mid++;
            }
            right++;
        }
        swap(nums[begin],nums[left-1]);
        if(k-1 >= left-begin && k-1 < mid-begin)
            return pivot;
        else if(k-1 < left-begin)
            return helper(nums,begin,left,k);
        else
            return helper(nums,mid,end,k-mid+begin);
    }
};

神奇的是，这个说好的平均$O(n)$算法比直接用stl的sort还慢。emmm，就这样吧。