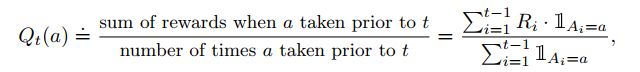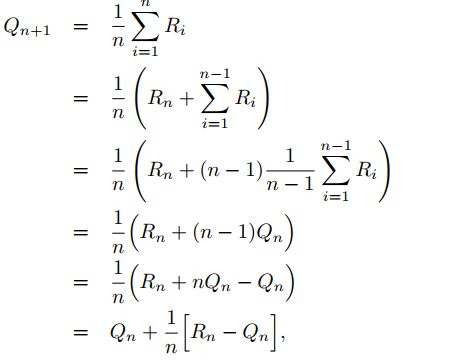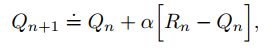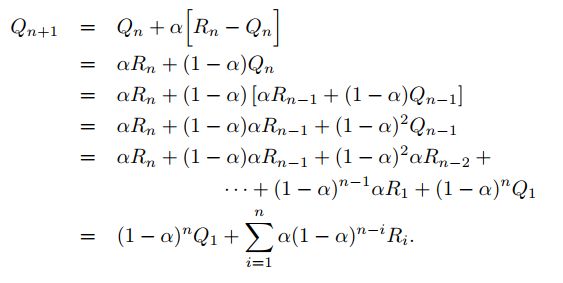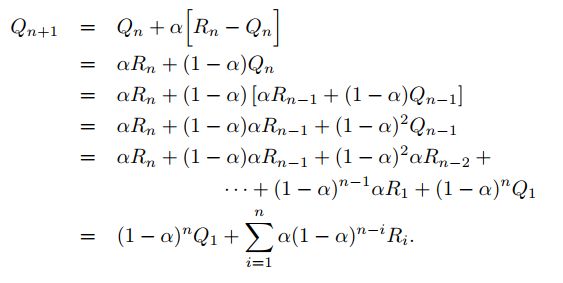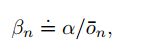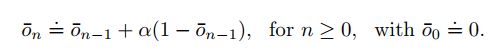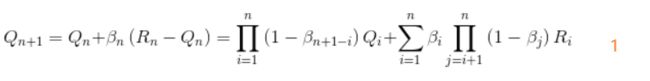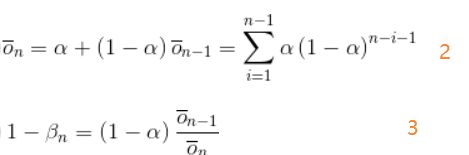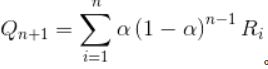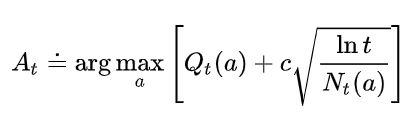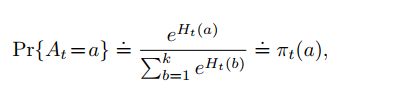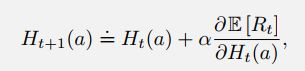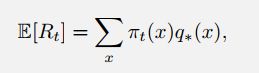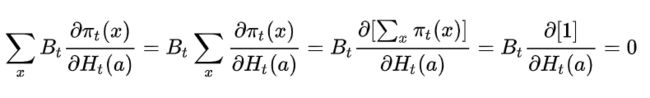2.多臂赌博机--阅读笔记【Reinforcement Learning An Introduction 2nd】

多臂赌博机

文章简要梳理：

• 介绍了行为值函数，这是一种基于tabular的rl解决方法。先提出了采样均值法来计算值函数，由于其计算量会随着时间的增长而增长，因此又提出了计算行为值函数的增量式实现方法。
• 但是又有一个问题，采样均值法仅仅适用于stationary的情况，如果要解决nonstationry情况下的行为值函数的求解计算，需要引入一个trick，即将step-size设定为一个常数α，但是会引入偏差，是一种有偏估计。
• trick one：设定optimistic initial value可以起到鼓励探索的作用（这一trick仅仅对于stationary是有效的，对于nonstationary是无效的.）
• 实现non-stationary情况下恒定步长的无偏估计，重新设置step-size，具体见文章内容3
• 接着又提到了一种平衡探索和利用的方法，UCB方法，这种方法是根据动作的不确定性进行选择的，尽管可以取得很好的效果，但是在nonstationary和高维状态空间的情况下实施起来比较复杂。
• 然后又提到了梯度赌博机方法，借助随机梯度算法根据action的preference进行选择。
• associative research方法

ε-greedy、optimistic initial values和UCB都可起到平衡exploration和exploitation的作用。

名称	描述	备注
行为值函数	基于tabular的rl解决方法
采样均值法	stationary
增量式实现	stationary
将step-size设定为常数	non-stationary	会引入偏差，是一种有偏估计
设置step-size	non-stationary	无偏估计（具体看文章内容）
optimistic initial value	仅仅对于stationary是有效的	可以起到鼓励探索的作用
UCB	stationary	推广应用比较复杂，是根据action的不确定性进行选择

前言

• 从本章开始，开始介绍基于表格的强化学习方法。这类方法适用于状态空间和动作空间小，可以将值函数表示为数组或者表格的形式。
• 强化学习与其他学习方法最明显的区别在于：强化学习利用训练信息即我们所设定的reward function 来评估我们所采取的动作，并不指导我们要采取什么动作。这就是RL需要探索的原因。评估式反馈evaluative feedback用来表明我们当前所采取的动作有多好，用来训练指示性反馈；指示性反馈instructive feedback用来指导算法采取哪个动作，但是并不需要真的采取这个动作才可以得到。
• 本章主要介绍单状态问题值函数的评估，借助evaluative feedback，单状态问题指的是只有一个状态，也就是策略不是状态的函数，是non-associative非关联的。本章所介绍的多臂赌博机问题是一个具有evaluative feedback的问题，并且是non-associative，可以理解为当前行为和下一次的行为是无关联的，是相互独立的。也就是说，当前我做出一个决策，任务over，下一次又是一个新的回合。但是对于完全强化学习来说，通常一个回合会涉及到多种决策。

k臂赌博机任务描述

假设有一台赌博机，上面有k个拉杆，每拉一个拉杆都会获得一定的奖励，不同的拉杆对应的奖励不同。我们的目标是在一定时间内通过执行拉杆动作来获得最大的收益。但前提是我们并不知道哪个拉杆对应的奖励大。因此这就需要通过探索来搞清楚每个拉杆对应的奖励情况。

行为值函数action-value function

要解决上面的问题，比较直接的方法就是我们评估拉动每个杆获得回报的期望值，然后选择期望值最大的那个就可以。因为每个拉杆都有一个期望奖励值，这个值代表了这个拉杆的好坏。在时间步长T步内，我们执行拉杆动作的行为表示为随机变量$A_t$,相应的回报为$R_t$,而选择某个动作a获得的期望值为$q_{\ast }(a)$。$R_t$就相当于是我们之前所说的evaluative feedback，而$q_{\ast }(a)$则相当于是instructive feedback。

q_*(a) = \mathbb{E}[R_t|A_t = a]

如果我们知道每个动作a对应的q值，那么决策就很容易做了，可惜没如果。那么我们把在时间t步时采取动作a的值估计记为$Q_t(a)$,这是一个估计值，这就是行为值函数。通过不断尝试并根据经验来更新该值。利用该值来选择动作，如果选择的动作是$A_t=argma{x}_a{Q}_t(a)$,此时所选择的策略是greedy策略，exploitive.但是刚开始由于我们的经验不足，所估计的值必定是不准确的，因此还需要进行一定的探索。可以采用$ϵ-greedy$的方法来平衡探索和利用。

把先估计行为的值，然后基于行为值再选择动作的方法记作动作值方法。选择某个动作时，这个动作的真实价值就是平均奖励，因此要估计这一点很自然的一种方法就是对实际收到的奖励取平均即可。

如果分母为0，直接令$Q_t(a)=0$即可。分子表示的是在t-1局的任务中，执行动作a所获得的奖励总和，分母表示的是t-1局任务中执行动作a的次数。根据大数定理，当玩的局数趋向于无穷大时，我们的估计值就会收敛到真实值$q_{\ast }(a)$。这种估计值函数的方法也叫做采样均值法（sample-average）。在得到了值函数之后，我们就可以得到采取某一action的估计价值，so我们应该遵循什么样的准则来选择动作呢？最简单的原则就是选择动作价值估计值最大的那个行为$A_t$即可，也就是采取greedy策略，but偶尔也会随机选择一个与值函数大小无关的行为，满足探索的需求，平衡探索和利用。当局数无限大时，那么每一个行为就会被抽样无限次，从而就可以保证对于所有的a，$Q_t(a)$都可以收敛到$q_{\ast }(a)$。

增量式实现方法

目前为止我们所使用的行为值方法是通过求所有观测回报值的均值来评估行为值函数，这就需要我们保存所有的观测值才可进行上述计算。随着训练步数的增长，导致内存逐渐增大，因此我们要考虑采用增量式的方法更加高效的求解动作值函数。对于动作a,$R_i$表示第i次选择该动作时获得的奖励值，$Q_n$表示是对$q_{\ast }$的第n次估计：

这个式子的含义就是第n+1次的值函数等于前一步对应的值函数加上一个差值，这个差值是估计误差，其中$1/n$是更新步长（step size）。更新的含义是缩小当前回报和估计值的误差）。比较一般的形式如下所示：

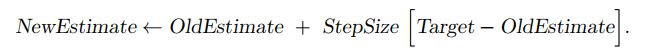Target-OldEstimate 是估计误差，通过向Target迈近一步来减小该误差。

使用增量式方法求解动作值函数的赌博机算法伪代码如下：

非平稳问题nonstationary problem

目前所探讨的采样均值的方法适用于稳态的赌博机问题，也就是说获得的回报的值或概率分布是不随时间变化的。实际上，我们所遇到的强化学习问题都是非稳态的。在这种情况下，应该做的是让最近的反馈比之前反馈的回报值所占的比重更大才合理。so,如何实现？结论是将步长step-size设置为一个常数。即用α替代之前的1/n；

为什么固定α就可以达到给最近回报较高的权重的效果呢？

如上所示，$Q_{n+1}$是之前所有回报的加权求和的形式。之所以叫做加权平均法是因为系数和为1.（可根据递归法证明）。我们看关于$R_i$，从$R_n$到$R_1$的系数变化分别是$\alpha ,\alpha (1-\alpha )...(1-\alpha {)}^2,(\alpha \in (0,1])$，权重大小是递减的。当前时刻越接近的R得到的权重越高。

常数步长的收敛问题：根据随机近似理论，要保证上式的迭代过程的收敛，需要满足两个基本条件：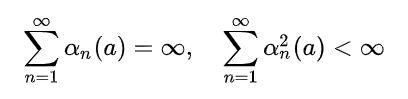

这两个约束条件有什么样的作用呢？第一个约束条件是为了保证能够克服初值所带来的误差以及各种随机干扰；第二个条件是为了保证算法最终的收敛。对于采样均值法来说上述的两个条件均满足，但是对于常数步长来说，只满足第一个条件。强化学习当中所遇到的环境多数情况下是nonstationary，上述约束条件尽管在理论上是比较完备的，但是在实际应用中很少用。另外，满足上述两个约束条件的步长step-size往往收敛十分缓慢。

乐观初值方法 optimistic initial values

观察这个式子可以得出对动作价值的估计受到初值$Q_1$的影响，通常初值是根据我们的经验自行设定的。因此估计的过程实际上是有偏估计，（渐进无偏）。合理的选择初值可以帮助算法更好的找到最优解。对于采样均值的方法来说，这个偏差会随着每个动作被选择的次数逐渐增加而消失，仅仅在第一次会带入误差。但是对于常数步长的方法来说，这个误差是始终存在的。实际上这种偏差并不是一个大问题，有时候反而是有利的，可以帮助探索。我们可以通过设定初始值来引入一些先验知识。

这里介绍的方法很简单，optimistic initial values，也就是在设置动作价值估计的初值时，选一个较大的数，这样可以保证收敛到真值的过程实际上是一个下降收敛的过程。怎么理解呢？我们假设最初所有动作的初值是一样的，因此我们最初会随机选择一个动作执行并更新动作价值估计值，更新之后，这个动作对应的q值就会下降，那么下次进行动作选择的时候就不会选择这个动作，而是从其余的动作当中选择一个动作，这样就很好的把探索和利用结合起来。

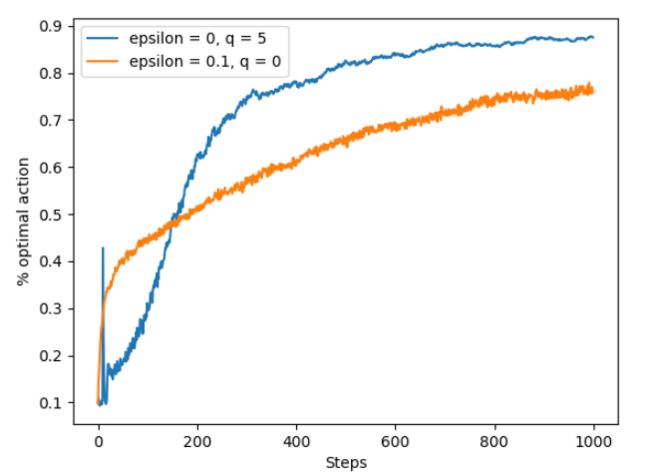
举个例子，对于后面的10-arm bandit实验，初始估计动作价值为0，倘若我们设置初始值为5。在我们的10-arm bandit实验当中，真实的回报值是来自均值为0，方差为1的高斯分布，也就是说，一次更新之后，更新的值函数一定小于5，所以算法就会再选择其他的行为，这样就实现了鼓励探索的过程。直到所有的行为都被更新了若干次之后，“exploitation”才会起作用。

如图，设置初始值为0，尽管起初greedy策略表现不是很好，这是因为它花费了一定的时间进行exploration，但是后来前者的表现要比后者好很多。尽管蓝色曲线采用的是greedy策略，但是由于引入乐观初值的方法，其探索效果要比基于探索策略得到的探索效果好很多。

注：这种方法仅仅对于stationary的情况适用，对于nonstationary问题基本是无效的，这是因为这种探索仅仅是暂时的，仅仅是针对初始的那一段时间，对于nonstationary，当回报分布发生改变时就需要重新探索，但是此时乐观初始值已经不再起作用了。

从上图分析，动作价值估计值q值设置为5并采取greedy的策略，刚开始会出现尖峰的原因：我们给定了一个较大的初值，最优动作的真值也较大，这样会导致初始误差小一点，最优动作返回的估计值较大，因此便会选择最优动作。随着最优动作被选择的次数增大，其估计值慢慢下降，此时就有可能再选择到其他动作。

exercise：无偏恒定步长trick：样本均值的方法虽然不会产生偏差但是不适用于nonstationary情况，但是大多数场景又是nonstationary的，因此要考虑采用固定步长，但是固定步长又会引入偏差，那么如何消除偏差呢？一种方法就是使用下述β作为step-size：

α是常规的步长表示，

证明：

${\beta }_1$等于α，把2 、3代入1中可得

​

证毕。

上限置信区间动作选择Upper-Confidence-Bound（UCB）

与ε-greedy和optimistic initial values类似，这是另一种平衡探索和利用的方式。ε-greedy方式存在一个问题就是对于当前并不属于最优的动作（次优）都一视同仁，怎么理解呢？就是当按照ε-greedy策略选择动作时，在进行探索时，除了最优的行为之外，其余的行为被选中的概率是均等的，因为是随机选择的。但是我们知道，在这些剩下的不是最优的行为当中，可能只有部分行为是有希望成为最优的。因此一个简单的想法就是根据这些次优的行为能够成为最优的潜力或者不确定性来设置进行探索的行为。

Action Selection

$N_t(a)$表示在时间t次之前动作a被选择的次数。c用来控制探索与利用之间的权重。整个表达式在原有估计q值的基础上加了一个开方项。这个开方项是对动作a的q值估计的不确定性度量。一个重要的问题：**为什么这个开方项就可以作为值函数对确定性估计的一个度量呢？**我们来看这个开方项，假设动作a从来没有被选择过，那么$N_t(a)$就是0，分母为0所以该项无限大，也就是说这个动作a的不确定性很大，这也符合逻辑，因为a从没有被选择过，显然这个时候argmax的结果就是选择当前的a；相应的，如果a被频繁的选择，那么开方项中的分母就会越来越大，那么这个动作对应的不确定性就小了。分子上的项是随着时间递增而递增的，不确定性也随之增长。如果当前算法遍历的状态越来越多，某个行为没有被选择过，那么它的相对不确定性就会增加。但是总的来说，分子变化带来的不确定性要小于分母变化带来的不确定性。

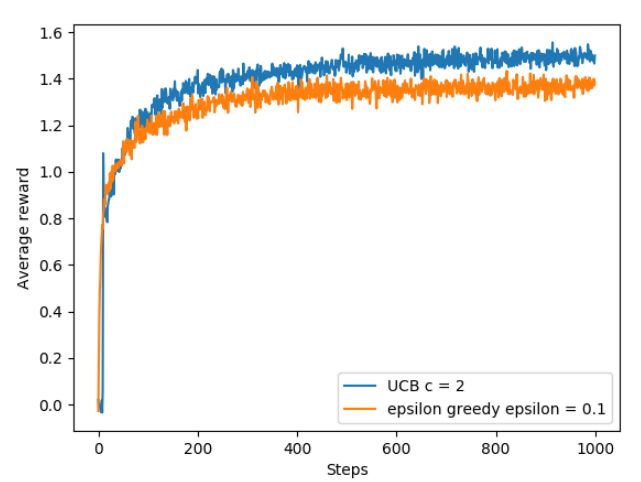
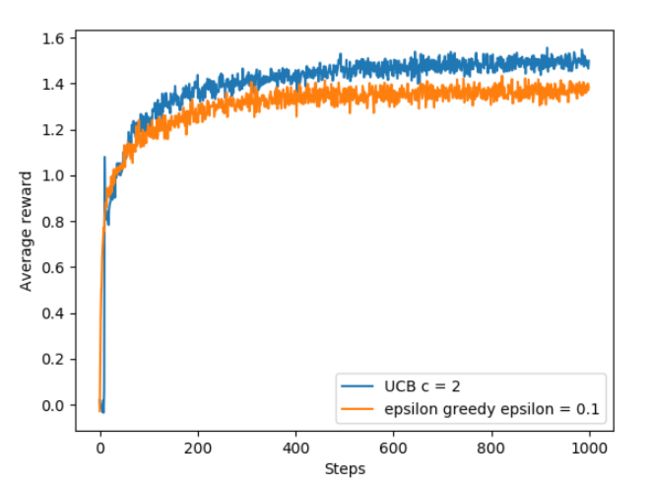
上图是基于下述的10-arm bandit实验，借助UCB和ε-greedy策略获得回报奖励的对比，UCB中c=2。尽管UCB的行为选择策略表现不错，但是推广应用起来比较复杂，一方面是因为nonstationary的挑战，另一方面是当状态空间维度较大时，这种策略实施起来就有些困难。在时间t内，某个动作的UCB与其Q值是正相关的，与其曾经被选择的次数是负相关的，实际选择的动作是用来权衡这两者的。

exercise：UCB中出现尖峰的原因：在选择到最优动作之前一直没有选择到这个动作，当逐渐积累了一定的UCB值之后，该最优动作被选择，被选择之后由于其返回的值很大，因此会被保持一段时间，但是随着该最优动作频繁的被选择，其UCB值会慢慢下降，从而使得算法有机会选择到其他的动作。

梯度赌博机算法

之前所采用的方法都是基于值函数的方式，通过构造的值函数对每个行为可获得期望回报的大小进行评估。某个动作对应的值函数越大那么就越有可能选择这个动作。实际上我们没有必要知道执行这个动作之后可以获得的回报具体值，我们只需要知道在时间t时，这个动作相比于其他动作的优势perference即可。根据这个信息就足以进行决策，因此这种策略梯度方法实际上是基于优势决策的方法。计算每个动作的perference，这里我们定义为$H_t(a)$，借助softmax分布或者叫做玻尔兹曼分布的方法来计算各个动作的概率。

${\pi }_t(a)$表示的是选择行为a的概率，实际上也就是一个policy。

Policy Update：一般情况下，RL问题的损失函数对应的优化目标就是期望得到的奖励值。如何更新这个perference function呢，实际上就是更新$H_t(a)$。

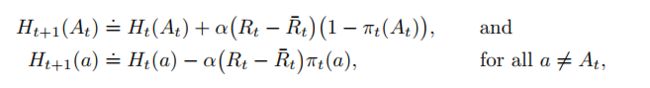
α表示step-size,${\overline{R}}_t$表示的是t时候之前获得的所有回报的均值。上面的式子是对当前行为$A_t$的更新，下面的式子是对之前从没有被选择过的行为a的更新。${\overline{R}}_t$起到了一个baseline的作用，在上式中，当前回报大于baseline，那么自然而然的后续我们要增大选择该动作的概率，下式中，既然都没有选择这个action，所获得的reward都比baseline大，那就没有必要选择了呗，所以就要减小选择这个动作的概率。

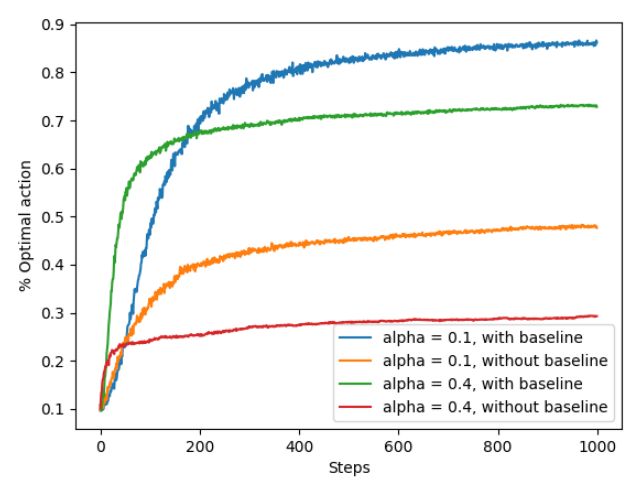
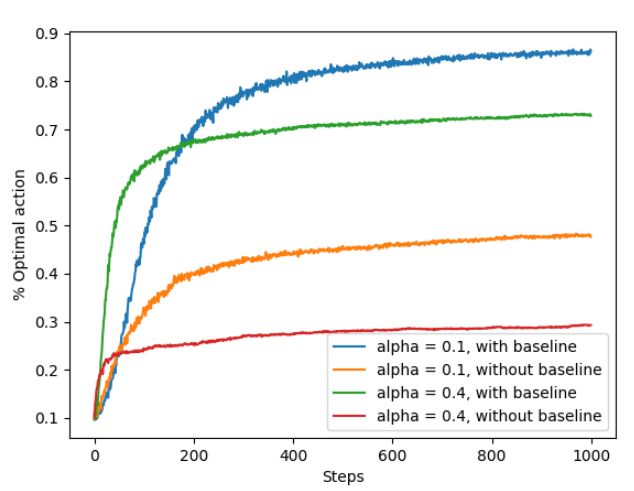
同样的，基于下述的10-arm bandit实验进行测试，得到的结果如下：

从图中可以明显的看出，with baseline的情况要比without baseline的情况好很多。实际上通过上图我们也可以看出α的选择对算法收敛也会产生一定影响。

上面的更新策略是根据什么得来的呢？答案是随机梯度优化。

推导过程：

我们可以根据随机梯度上升法获得上面两个更新公式的结论。根据梯度上升法，每个行为a的更新可以表示为：

​

​

​

为什么会突然多出一个$B_t$，形式上是为了凑出更新公式当中的平均奖励那一项，为什么可以用来凑呢？看下面这个式子：

等于0，自然没有任何影响。但是要注意凑出来的这一项不能与动作a有关，否则的话就没有办法消掉了。其实这一项就是充当baseline的角色。

​
最后改写成增量的形式就是：

​ .

​ 的推导过程如下：

baseline的作用可以这样理解，这个动作当前得到的回报比之前获得的回报均值都大，也就是当前动作的回报值大于之前回报的整体平均水平，那么我们就增加执行这个动作的概率。

关联/联想搜索（情景式赌博）associative research

对于我们之前所讲的bandit问题，有一个特点就是只有一个情景。就是每次下注之前的场景都是一样的，所以说每次下注之前你无需关心当前你所处的情景/状态，因为是单状态，你只关心拉下哪个arm可以获得高额奖励，这种问题叫做non-associative，无联想的赌博问题。实际中，rl的相关问题会遇到多种情景，这时候不仅需要考虑采用什么样的动作会获得高额回报，同时还需要考虑在哪种状态下/哪种情境下对应的哪个行为更好。这种situation称作是associative联想式的问题。举个简单的例子，当你走进澳门赌场，倘若你始终在一张赌桌上下赌注，那么这种situation就属于是单状态non-associative的，你只需要考虑在这种赌桌上如何获取最大的收益即可。倘若你并不是在一张赌桌上下赌注，而是游走于各种赌博游戏之间，那么现在你首先要考虑的是该选择哪张赌桌或者哪个赌博游戏，选定这一步之后你才能在这个的基础上选择动作从而获得最大收益。这种situation是属于associative的。

扩展之前的赌博机例子，现在又多台赌博机，每个赌博机的回报分布是不一样的，现在的任务是在这多台赌博机上下赌注，以期获得最大的回报。这就是一个associative问题了，也叫做contextual bandit情景式赌博。我们不仅需要选择最好的arm同时还要选择使用哪台赌博机，这个最优动作arm selection与某台赌博机是相互关联起来的。这就是associative research中的associative的含义。

这个情景式赌博问题似乎已经和完全强化学习很接近，但实际上它是介于完全强化学习和k-arm bandits问题之间的。之所以说它像强化学习问题是因为它涉及到策略，不同于rl的是它的当前状态不会影响下一个状态和回报，状态与状态之间是相互独立的。

总结

本章以多臂赌博机问题为例，介绍了强化学习中基于tabular的action value方法来解决rl问题。为了平衡探索和利用我们引入了ε-greedy策略、UCB策略。基于UCB策略进行探索时可以考虑到每个行为的确定性，某个行为的不确定性越大越有可能被选择。另外一个trick就是设置一个optimistic initial value，有时其探索效果甚至比ε-greedy策略还要好。另外还介绍了基于偏好perference的策略梯度算法。最后介绍了associative research关联搜索。

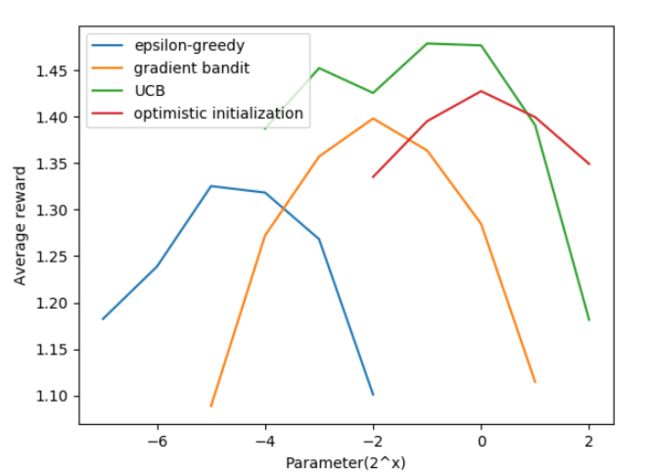
为了公平的比较上述算法的效果，我们比较不同算法在不同参数下的表现，这一手段称作参数研究parameter study。

如上图的学习曲线图，所有的算法基本都是中间值效果较好。图中UCB算法效果较好。

对于k-armed bandit问题，用Gittins index(基于贝叶斯方法，根据先验选择最好动作，然后计算后验作为下一个step的先验，常采用posterior sampling or Thompson sampling处理分布)计算值函数是最好的探索和利用的权衡，但是要求分布已知且计算量较大，因此很难扩展。它和本章中distribution-free方法中最好情况是差不多的。在贝叶斯方法中，对每个动作先验分布，如果知道每个动作导致的reward分布，就可以计算后验了。但对于离散问题，树状结构指数级扩大，导致开销不能接受。但是或许这能用估计的方法逼近，把bandit方法转换为标准RL问题。

10臂赌博机实验

实验描述：10 arm赌博机问题表明有10个动作，每个动作都对应一个奖励分布，每次执行该动作所获得的奖励是从其对应的分布上采样。初始化时首先从一个正态分布N（0，1）上随机采样10个值作为10个动作奖励分布的均值，也就是10个$q_{\ast }(a)$，然后设置每个动作都服从N（$q_{\ast }(a)$，1）的分布。为了衡量算法的效果，按照上述的步骤生成2000个10 arm赌博机问题，每个都仿真1000step，然后取这2000个问题上的均值来衡量算法的效果。参考github DEMO：

class Bandit:
    # @k_arm: # of arms
    # @epsilon: probability for exploration in epsilon-greedy algorithm
    # @initial: initial estimation for each action
    # @step_size: constant step size for updating estimations
    # @sample_averages: if True, use sample averages to update estimations instead of constant step size
    # @UCB_param: if not None, use UCB algorithm to select action
    # @gradient: if True, use gradient based bandit algorithm
    # @gradient_baseline: if True, use average reward as baseline for gradient based bandit algorithm
    def __init__(self, k_arm=10, epsilon=0., initial=0., step_size=0.1, sample_averages=False, UCB_param=None,
                 gradient=False, gradient_baseline=False, true_reward=0.):
        self.k = k_arm
        self.step_size = step_size
        self.sample_averages = sample_averages
        self.indices = np.arange(self.k)
        self.time = 0
        self.UCB_param = UCB_param
        self.gradient = gradient
        self.gradient_baseline = gradient_baseline
        self.average_reward = 0
        self.true_reward = true_reward
        self.epsilon = epsilon
        self.initial = initial

    def reset(self):
        # real reward for each action
        self.q_true = np.random.randn(self.k) + self.true_reward

        # estimation for each action
        self.q_estimation = np.zeros(self.k) + self.initial

        # # of chosen times for each action
        self.action_count = np.zeros(self.k)

        self.best_action = np.argmax(self.q_true)

        self.time = 0

    # get an action for this bandit
    def act(self):
        if np.random.rand() < self.epsilon:
            return np.random.choice(self.indices)

        if self.UCB_param is not None:
            UCB_estimation = self.q_estimation + \
                self.UCB_param * np.sqrt(np.log(self.time + 1) / (self.action_count + 1e-5))
            q_best = np.max(UCB_estimation)
            return np.random.choice(np.where(UCB_estimation == q_best)[0])

        if self.gradient:
            exp_est = np.exp(self.q_estimation)
            self.action_prob = exp_est / np.sum(exp_est)
            return np.random.choice(self.indices, p=self.action_prob)

        q_best = np.max(self.q_estimation)
        return np.random.choice(np.where(self.q_estimation == q_best)[0])

    # take an action, update estimation for this action
    def step(self, action):
        # generate the reward under N(real reward, 1)
        reward = np.random.randn() + self.q_true[action]
        self.time += 1
        self.action_count[action] += 1
        self.average_reward += (reward - self.average_reward) / self.time

        if self.sample_averages:
            # update estimation using sample averages
            self.q_estimation[action] += (reward - self.q_estimation[action]) / self.action_count[action]
        elif self.gradient:
            one_hot = np.zeros(self.k)
            one_hot[action] = 1
            if self.gradient_baseline:
                baseline = self.average_reward
            else:
                baseline = 0
            self.q_estimation += self.step_size * (reward - baseline) * (one_hot - self.action_prob)
        else:
            # update estimation with constant step size
            self.q_estimation[action] += self.step_size * (reward - self.q_estimation[action])
        return reward


def simulate(runs, time, bandits):
    rewards = np.zeros((len(bandits), runs, time))
    best_action_counts = np.zeros(rewards.shape)
    for i, bandit in enumerate(bandits):
        for r in trange(runs):
            bandit.reset()
            for t in range(time):
                action = bandit.act()
                reward = bandit.step(action)
                rewards[i, r, t] = reward
                if action == bandit.best_action:
                    best_action_counts[i, r, t] = 1
    mean_best_action_counts = best_action_counts.mean(axis=1)
    mean_rewards = rewards.mean(axis=1)
    return mean_best_action_counts, mean_rewards

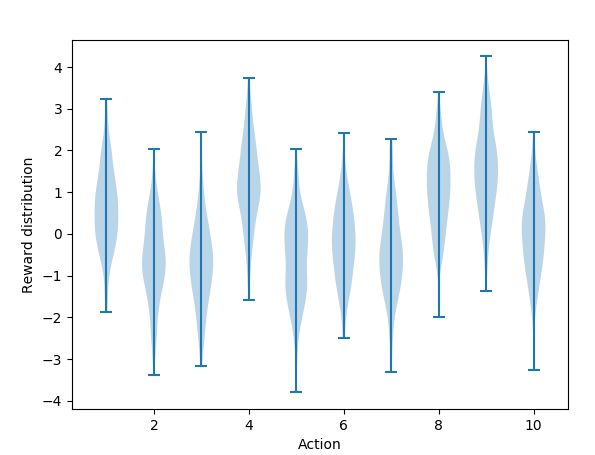
1. 小提琴图-每个动作的动作估计值分布

如上述小提琴图所示，蓝色部分表示的是采取每个动作所获得的动作值分布。

def figure_2_1():
    plt.violinplot(dataset=np.random.randn(200, 10) + np.random.randn(10))
    plt.xlabel("Action")
    plt.ylabel("Reward distribution")
    plt.savefig('../images/figure_2_1.png')
    plt.close()

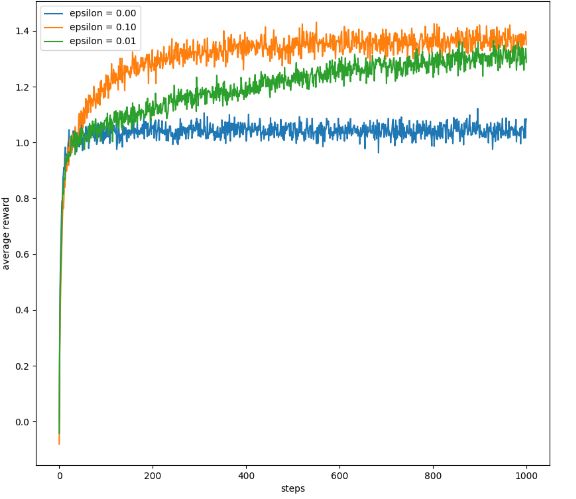
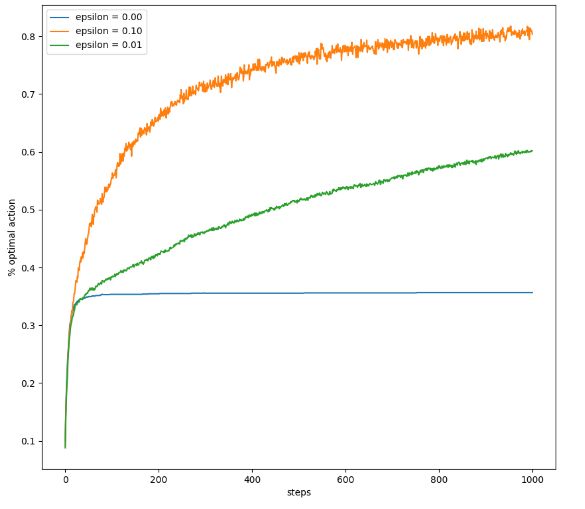
2. 探索率对算法性能的影响

接着我们来看一下探索率的大小$ϵ$对算法性能的影响：

def figure_2_2(runs=2000, time=1000):epsolion
    epsilons = [0, 0.1, 0.01]
    bandits = [Bandit(epsilon=epes, sample_averages=True) for eps in epsilons]
    best_action_counts, rewards = simulate(runs, time, bandits)
    plt.figure(figsize=(10, 20))

    plt.subplot(2, 1, 1)
    for eps, rewards in zip(epsilons, rewards):
        plt.plot(rewards, label='epsilon = %.02f' % (eps))
    plt.xlabel('steps')
    plt.ylabel('average reward')
    plt.legend()

    plt.subplot(2, 1, 2)
    for eps, counts in zip(epsilons, best_action_counts):
        plt.plot(counts, label='epsilon = %.02f' % (eps))
    plt.xlabel('steps')
    plt.ylabel('% optimal action')
    plt.legend()

    plt.savefig('../images/figure_2_2.png')
    plt.close()

• 该图反映的是采用不同的$ϵ$，episode-avg. reward的曲线图。从图中可以看到，当具有一定的探索概率时，agent可以获得的平均奖励更大。

• 该图反映了采取不同$ϵ$时，step与选择最优动作百分比之间的关系曲线。最优动作百分比的含义是每个step中实际选择最优动作的次数与总步数的百分比。可以看出贪婪算法有约35%的比例选择了最优行为，容易陷入局部最优的情况。对于探索策略可以达到60%-85%，探索率越大曲线上升快，找到全局最优动作的时间少。

通过上面的实验验证我们看出，有搜索策略的方式更好，倘若是对于确定性环境，也就是说每采取某个动作所获得的回报值是固定的，并不是一个分布。此时贪婪策略可能更好，因为只需要遍历一次动作就可以得到最优值。总之，在强化学习中探索和利用之间的平衡对算法的表现有很大的影响。

3. optimistic initial value

def figure_2_3(runs=2000, time=1000):
    bandits = []
    bandits.append(Bandit(epsilon=0, initial=5, step_size=0.1))
    bandits.append(Bandit(epsilon=0.1, initial=0, step_size=0.1))
    best_action_counts, _ = simulate(runs, time, bandits)

    plt.plot(best_action_counts[0], label='epsilon = 0, q = 5')
    plt.plot(best_action_counts[1], label='epsilon = 0.1, q = 0')
    plt.xlabel('Steps')
    plt.ylabel('% optimal action')
    plt.legend()

    plt.savefig('../images/figure_2_3.png')
    plt.close()

相关分析见前面关于optimistic initial value的内容

4. UCB

def figure_2_4(runs=2000, time=1000):
    bandits = []
    bandits.append(Bandit(epsilon=0, UCB_param=2, sample_averages=True))
    bandits.append(Bandit(epsilon=0.1, sample_averages=True))
    _, average_rewards = simulate(runs, time, bandits)

    plt.plot(average_rewards[0], label='UCB c = 2')
    plt.plot(average_rewards[1], label='epsilon greedy epsilon = 0.1')
    plt.xlabel('Steps')
    plt.ylabel('Average reward')
    plt.legend()

    plt.savefig('../images/figure_2_4.png')
    plt.close()

相关分析见前面关于UCB的内容

5. 梯度赌博机方法

def figure_2_5(runs=2000, time=1000):
    bandits = []
    bandits.append(Bandit(gradient=True, step_size=0.1, gradient_baseline=True, true_reward=4))
    bandits.append(Bandit(gradient=True, step_size=0.1, gradient_baseline=False, true_reward=4))
    bandits.append(Bandit(gradient=True, step_size=0.4, gradient_baseline=True, true_reward=4))
    bandits.append(Bandit(gradient=True, step_size=0.4, gradient_baseline=False, true_reward=4))
    best_action_counts, _ = simulate(runs, time, bandits)
    labels = ['alpha = 0.1, with baseline',
              'alpha = 0.1, without baseline',
              'alpha = 0.4, with baseline',
              'alpha = 0.4, without baseline']

    for i in range(len(bandits)):
        plt.plot(best_action_counts[i], label=labels[i])
    plt.xlabel('Steps')
    plt.ylabel('% Optimal action')
    plt.legend()

    plt.savefig('../images/figure_2_5.png')
    plt.close()

相关分析见前面关于梯度赌博机方法的内容

6. 算法比较

def figure_2_6(runs=2000, time=1000):
    labels = ['epsilon-greedy', 'gradient bandit',
              'UCB', 'optimistic initialization']
    generators = [lambda epsilon: Bandit(epsilon=epsilon, sample_averages=True),
                  lambda alpha: Bandit(gradient=True, step_size=alpha, gradient_baseline=True),
                  lambda coef: Bandit(epsilon=0, UCB_param=coef, sample_averages=True),
                  lambda initial: Bandit(epsilon=0, initial=initial, step_size=0.1)]
    parameters = [np.arange(-7, -1, dtype=np.float),
                  np.arange(-5, 2, dtype=np.float),
                  np.arange(-4, 3, dtype=np.float),
                  np.arange(-2, 3, dtype=np.float)]

    bandits = []
    for generator, parameter in zip(generators, parameters):
        for param in parameter:
            bandits.append(generator(pow(2, param)))

    _, average_rewards = simulate(runs, time, bandits)
    rewards = np.mean(average_rewards, axis=1)

    i = 0
    for label, parameter in zip(labels, parameters):
        l = len(parameter)
        plt.plot(parameter, rewards[i:i+l], label=label)
        i += l
    plt.xlabel('Parameter(2^x)')
    plt.ylabel('Average reward')
    plt.legend()

    plt.savefig('../images/figure_2_6.png')
    plt.close()

相关分析见前面总结部分的内容