大规模数据相似度计算时,解决数据倾斜的问题的思路之一(分块思想)
现有user、item矩阵,如何计算两两用户的相似度呢?最直接的方法就是夹角余弦,计算用户向量之间的cos值,来度量相似度。因为实际问题中,矩阵通常是很稀疏的,所以真正实现cos计算相似度计算的时候,为了减少计算量,采用的的是倒排索引的数据结构。即:
虽然采用的倒排的结构,但是用户量和item量很大,且有些item对应的用户量很大的时候,就会出现严重的数据倾斜问题。以MapReduce实现过程为例,如果大多数item对应用户量都是几十万的级别,少量item对应user量很大,例如百万以上,则聚集到这些item上(即对应的reduce上)的数据量就会很大,此时就出现数据倾斜的问题,整体速度方面就会很慢。如何解决这种数据倾斜的问题呢?
解决上面提到的数据倾斜问题,可采用矩阵分块的思想,当一个item下用户量特别大,将其打散到多个reduce当中进行处理,可大大增加运行的速度。但带来的负面影响就是,网络通信量增加,分k块,通信量就增加原始数据量的k倍。实际运行的时候,可以多种权衡,例如下面这种:
1) 当item的用户量不大的时候(设定一个阈值),即小于阈值,则不进行分块
2) 当item对应用户量比较大的时候,可以分k1块
3) 当item对应用户量特别大的时候,可以分k2块,这里k2>k1
简单起见,下面介绍固定分块的思路:
假定分5块,即一个item对应的用户分五块,在多个reduce里面完成相似度的计算。伪代码如下:
userinfo.set(0, 用户id);
userinfo.set(1, item id);
userinfo.set(2, value);
int index = (int) (user_id % blocks);
System.out.println("map阶段,取模分块:\t" + blocks);
/*下面的if、else,保证了只计算上三角矩阵(因为这里的关系是双向)
同时,注意要实现Comparator,保证不同flag的key是有序到reduce中*/
for (int i = 0; i < blocks; i++) {
if (index <= i) {
key.setKeyPrior(item + "_A" + index + "A" + i, 1);
flag.set(1);
userinfo.set(3, flag);
} else if (index > i) {
key.setKeyPrior(item + "_A" + i + "A" + index, 2);
flag.set(2);
userinfo.set(3, flag);
}
context.write(key, userinfo);
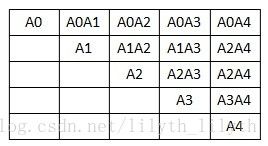
}分块直观效果如下图:
在reduce中,要处理两种情况,一种是对角线对应矩阵的用户相似度计算,另外一种情况是上三角其他两两矩阵用户相似度的计算。
(1)对角线的矩阵相似度计算时:可采用容器存储所有用户信息,然后:
for (int i = 0; i < this.userList.size(); i++) {
user1 = this.userList.get(i));
for (int j = i + 1; j < this.userList.size(); j++) {
user2 = this.userList.get(j));
计算相似度...
}
}(2)上三角其他两两矩阵用户相似度的计算时:
先把前面矩阵存储到容器中,后面矩阵的每条记录,计算其和容器矩阵中所有用户的相似度,以A1A2为例,先将A1存储到容器,然后每收到一条记录,则计算其和A1中用户相似度。这里两点特别注意:
- 在上面第二种情况中,不需要计算A1中所有用户两两用户相似度,只需要计算A2和A1中两两用户相似度
- 要实现Comparator,例如PriorKeyComparator,保证不同flag的key是有序到reduce中。job.setOutputValueGroupingComparator(PriorKeyComparator.class);
这种分块的思想可以解决数据倾斜加快速度。但是当数据量特别大的时候,即用户量上千万甚至上亿,速度是很大的瓶颈。现在解决这种问题的思路是,通过GMM这种软聚类的方法,同一个top k类别的用户,才能关联的起来,减少计算量从而加快速度。