FM模型解读

最近在公司一直在搞FM及FFM模型优化，也做了几把实验，但是对FM模型的原理仍是一知半解，理解的不是很透彻，加上最近又开始找工作了，因此对FM模型做下梳理加深理解。

一.FM

FM解决的问题：大规模稀疏数据下的特征组合问题。

1. 为什么要特征组合：
   实践中通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。例如“USA”与“Thanksgiving”，“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等。因此，引入两个特征的组合是非常有意义的。
2. 如何组合：
   数学模型上表达特征xi与xj的组合用X_iX_j表示，即所说的多项式模型，通常情况下只考虑二阶多项式模型，也就是特征两两组合的问题。二阶多项式的模型如下：
   
   （这个公式是二阶多项式的模型，算作是FM模型的雏形吧）。其中，n 代表样本的特征数量，这里的特征是离散化后的特征，如city=’BeiJing’，X_i 是第 i 个特征的值，W₀、W_i、W_ij 是模型参数。从公式来看，模型前半部分就是普通的LR线性组合，后半部分的交叉项即特征的组合。单从模型表达能力上来看，FM的表达能力是强于LR的，至少不会比LR弱，当交叉项参宿全为0时即退化为普通的LR模型。
   从这个式子中可以看出，组合特征的参数一共有1+2+….+(n-1) =n(n−1)/2 个，其中的n是特征维度（这里的特征是指离散化后的特征，如city=‘北京’），任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，交叉项参数的训练是很困难的。其原因是，每个参数 W_ij 的训练需要大量 Xi 和Xj特征同时非零的样本；由于样本数据本来就比较稀疏，满足“Xi 和 Xj 都非零”的样本将会非常少。训练样本的不足，很容易导致参数 Wij 不准确，最终将严重影响模型的性能。
3. 如何求解二次项参数W_ij：
   W_ij求解的思路是通过矩阵分解的方法。所有的二次项参数W_ij可以组成一个对称阵W（为了方便说明FM的由来，对角元素可以设置为正实数），那么这个矩阵就可以分解为 W=V^TV，V 的第 i 列便是第 i 维特征的隐向量。换句话说，特征分量Xi与Xj的交叉项系数就等于Xi对应的隐向量与Xj对应的隐向量的内积，即每个参数 w_ij=⟨vi,vj⟩，这就是FM模型的核心思想。V i表示 X i 的隐向量, V j 表示 X j 的隐向量 ，为了求出 W_ij, 我们需要求出特征分量 X_i 的辅助向量 Vi=(V_i1……V_ik)， X_j 的辅助向量 Vj=(V_j1……V_jk)，k表示隐向量长度（ 实际应用中k<< n）,转换过程如下图所示。

W∗=⎡⎣⎢⎢⎢⎢⎢⎢w11w21w31⋮wn1w12w22w32⋮wn2⋯⋯⋯⋱⋯w1nw2nw3n⋮wnn⎤⎦⎥⎥⎥⎥⎥⎥=VTV=⎡⎣⎢⎢⎢⎢V1V2⋮Vn⎤⎦⎥⎥⎥⎥[V1V2⋯Vn]=⎡⎣⎢⎢⎢⎢v11v21⋮vn1V12V22⋮Vn2⋯⋯⋱⋯V1kV2k⋮Vnk⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢v11v12⋮v1kV21V22⋮V2k⋯⋯⋱⋯Vn1Vn2⋮Vnk⎤⎦⎥⎥⎥⎥

W ^*矩阵对角线上面的元素即为交叉项的参数。

经过上面公式，二次项的参数数量由原来的n(n−1)/2个W_in减少为 kn个W_ik，远少于多项式模型的参数数量。另外，参数因子化使得 X_hX_i的参数和 X_hX_j 的参数不再是相互独立的，因为有了X_h特征关联。因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说， X_hX_i 和 X_iX_j 的系数分别为 ⟨vh,vi⟩ 和 ⟨vi,vj⟩，它们之间有共同项 **v**i。也就是说，所有包含“Xi 的非零组合特征”（存在某个 j≠i，使得 XiXj≠0）的样本都可以用来学习隐向量 **V**i，这很大程度上避免了数据稀疏性造成的影响。而且隐向量可以表示之前没有出现过的交叉特征，假如在数据集中经常出现<男，篮球> ，<女,化妆品>，但是没有出现过<男，化妆品>，<女，篮球>，这时候如果用Wij表示<男，化妆品>的系数，就会得到0。但是有了男特征和化妆品特征的隐向量之后，就可以通过来求解 <V男,V化妆品> 来求解，就是如此amazing。。
4. 如何求解FM:
经过3的推导之后二次多项式模型就可以写成如下形式：

y=w0+∑i=1nwixi+∑i=1n−1∑j=i+1nwijxixj=w0+∑i=1nwixi+∑i=1n−1∑j=i+1n<Vi,Vj>xixj=12(∑i=1n∑j=1n<Vi,Vj>xixj−∑j=1n<Vi,Vj>xixj)=12(∑i=1n∑j=1n∑f=1kvi,fvj,fxixj−∑i=1n∑f=1kvi,fvi,fxixi)=12∑i=1k{(∑i=1nvi,fxi)(∑j=1nvj,fxj)−∑i=1nv2i,fx2i}=12∑f=1k{(∑i=1nvi,fxi)2−∑i=1nv2i,fx2i}(FM)

此处解释下推导公式，第三个等号，对称矩阵W对角线上半部分的和等于(整个矩阵的和-对角线上的和 )/2,对角线表示特征自己和自己组合，除以2是因为对称。第四个等号是把向量Vi,Vj內积展开成累加和的形式。第五个等号提出公共部分。最后一个等号是i和j相当于是一样的，表示成平方过程。
5. 复杂度分析：
直观上看，FM的复杂度是 O(kn ²)。但是，通过上面公式的等式，FM的二次项可以化简，最后只与 v _i,f 有关,因此其复杂度是 O(kn)。由此可见，FM可以在线性时间对新样本作出预测，复杂度和ＬＲ模型一样，但是效果上缺提升不少。

在训练ＦＭ时，假如用ＳＧＤ来优化模型，训练时各个参数的梯度如下，

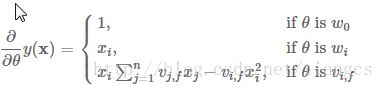
θ是模型参数，v_i,f是隐向量V_i的第f个元素，由于
∑nj=1vj,fxj 只与f有关，只要求出一次所有的f元素，就能够计算出所有 vi,f 的梯度，而f是矩阵V中的元素，显然计算所有f的复杂度是O(kn),当已知 ∑nj=1vj,fxj 时计算每个参数梯度的复杂度是O(1),更新每个参数的复杂度是O(1),因此训练FM模型的复杂度也是O(kn)。
6. 关于隐向量V：这里的Vi是特征Xi的低纬稠密表达，实际中隐向量的长度通常远小于特征维度N,在我做的实验中长度都是4。在实际的CTR场景中，数据都是很稀疏的category特征，通常表示成离散的one-hot形式，这中编码方式，使得one-hot vector非常长，而且很稀疏，同时特征总量也骤然增加，达到千万级甚至亿级别都是有可能的，而实际上的category特征数目可能只有几百维。FM学到的隐向量可以看做是特征的一种embedding表示，把离散特征转化为Dense Feature，这种Dense Feature还可以后续和DNN来结合，作为ＤＮＮ的输入，事实上用于DNN的CTR也是这个思路来做的。关于FM和DNN的结合，后续有时间在更吧。。。

二.FFM

FFM场感知分解机器（Field-aware Factorization Machine ，简称FFM）最初的概念来自于Yu-Chin Juan与其比赛队员，它们借鉴了辣子Michael Jahrer的论文中field概念，提出了FM的升级版模型。
通过引入field的概念，FFM把相同性质的特征归于同一个field。比如Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征都是代表日期的，可以放到同一个field中。同理，假如商品的品类编码生成了550个特征，这550个特征都是说明商品所属的品类，因此它们也可以放到同一个field中。那么，我们可以把同一个categorical特征经过one-hot编码生成的数值型特征都可以放在同一个field中。
在FFM中，每一维特征 xi，针对其它特征的每一种field fj，都会学习一个隐向量 V_i,fj。因此，隐向量不仅与特征相关，也与特征xj所属的field相关，这与每个域的内在差异有关。

其中，fj 是第 j 个特征所属的field。如果隐向量的长度为 k，那么FFM的二次参数有 nfk 个，远多于FM模型的 nk 个。此外，由于隐向量与field相关，FFM二次项并不能够化简，其预测复杂度是 O(kn2)。
举个例子 xi 特征(field 5)：0.03 1:0.1,0.2,0.3,0.4 2:0.5,0.6,0.7,0.8
xj特征(field 2)： 0.01 3:0.01,0.02,0.03,0.04
其中隐向量大小是4，则V_i,fj=<0.5,0.6,0.7,0.8> , V_j,fi=<> ，xj学到的xi隐向量为空。

参考链接：

http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/6340129.html
http://blog.csdn.net/bitcarmanlee/article/details/52143909
https://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html
http://www.csie.ntu.edu.tw/~b97053/paper/Factorization%20Machines%20with%20libFM.pdf
http://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf