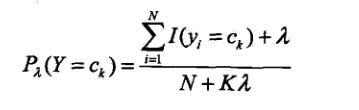分类算法:朴素贝叶斯算法
一、问题的提出
使用Wikipedia上的一个例子:
“一所学校里面有 60% 的男生,40% 的女生。男生总是穿长裤,女生则一半穿长裤一半穿裙子。有了这些信息之后我们可以容易地计算“随机选取一个学生,他(她)穿长裤的概率和穿裙子的概率是多大”,这个就是前面说的“正向概率”的计算。然而,假设你走在校园中,迎面走来一个穿长裤的学生(很不幸的是你高度近似,你只看得见他(她)穿的是否长裤,而无法确定他(她)的性别),你能够推断出他(她)是男生的概率是多大吗?”
我们来算一算:假设学校里面人的总数是 U 个。60% 的男生都穿长裤,于是我们得到了 U * P(Boy) * P(Pants|Boy) 个穿长裤的(男生)(其中 P(Boy) 是男 生的概率 = 60%,这里可以简单的理解为男生的比例;P(Pants|Boy) 是条件概率,即在 Boy 这个条件下穿长裤的概率是多大,这里是 100% ,因为所有男生都穿长裤)。40% 的女生里面又有一半(50%)是穿长裤的,于是我们又得到了 U * P(Girl) * P(Pants|Girl) 个穿长裤的(女生)。加起来一共是 U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl) 个穿长裤的,其中有 U * P(Girl) * P(Pants|Girl) 个女生。两者一比就是你要求的答案。下面我们把这个答案形式化一下:我们要求的是 P(Girl|Pants) (穿长裤的人里面有多少女生),我们计算的结果是 U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)] 。容易发现这里校园内人的总数是无关的,可以消去。于是得到
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
注意,如果把上式收缩起来,分母其实就是 P(Pants) ,分子其实就是 P(Pants, Girl) 。而这个比例很自然地就读作:在穿长裤的人( P(Pants) )里面有多少(穿长裤)的女孩( P(Pants, Girl) )。
进一步得到公式的一般形式:
P(B|A) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]
收缩起来就是:P(B|A) = P(AB) / P(A)
其实这个就等于:P(B|A) * P(A) = P(AB)
二、正式的定义
朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法,然后依据被分类项属于各个类的概率,概率最大者即为所划分的类别。
设输入空间X=(x1,x2,x3...xn),输出类标记为Y=(y1,y2,y3...yn)。x的集合记为X,称为属性集。一般X和Y的关系不确定的,你只能在某种程度上说x有多大可能性属于类y1,比如说x有80%的可能性属于类y1,这时可以把X和Y看做是随机变量,P(Y|X)称为Y的后验概率(posterior probability),与之相对的P(Y)称为Y的先验概率(prior probability),P(X=x|Y=y1)称之为条件概率。
简单说来就是:贝叶斯分类算法的理论基于贝叶斯公式,P(B|A)=(P(A|B)P(B))/P(A) ,其中P(A|B)称为条件概率,P(B)先验概率,对应P(B|A)为后验概率。朴素贝叶斯分类器基于一个简单的假定,即给定的目标值属性之间是相互独立。贝叶斯公式之所以有用是因为在日常生活中,我们可以很容易得到P(A|B),而很难得出P(B|A),但我们更关心P(B|A),所以就可以根据贝叶斯公式来计算。
三、应用举例
如下表所示,训练数据学习一个朴素贝叶斯分类器并确定x=(2,S)T的类标记y。表中x1、x2为特征,取值的集合分别为X1={1,2,3},X2={S,M,L},类标记Y={1,-1}
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| X1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
| X2 | S | M | M | S | S | S | M | M | L | L | L | M | M | L | L |
| Y | -1 | -1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 |
根据贝叶斯算法得到如下概率:
P(Y=1)=9/15,P(Y=-1)=6/15
P(X1=1|Y=1)=2/9,P(X1=2|Y=1)=3/9,P(X1=3|Y=1)=4/9
P(X2=S|Y=1)=1/9,P(X2=M|Y=1)=4/9,P(X2=L|Y=1)=4/9
P(X1=1|Y=-1)=3/6,P(X1=2|Y=-1)=2/6,P(X1=3|Y=-1)=1/6
P(X2=S|Y=-1)=3/6,P(X2=M|Y=-1)=2/6,P((X2=L|Y=-1)=1/6
所以对于给定的x=(2,S)T计算:
P(Y=1)P(X1=2|Y=1)P(X2=S|Y=1)=(9/15)(3/9)(1/9)=1/45
P(Y=-1)P(X1=2|Y=-1)P(X2=S|Y=-1)=(6/15)(2/6)(1/6)=1/15
所以分类结果为y=-1
拉普拉斯平滑(Laplace smoothing):由于概率计算中间可能会出现所要估计概率值为0的情况,进而使得后验概率的计算结果受到影响,使分类结果产生偏差,所以会采用Laplace校准
如此以来,对于上面的问题,按照拉普拉斯平滑后估计概率为:(入=1)
P(Y=1)=10/17,P(Y=-1)=7/17
P(X1=1|Y=1)=3/12,P(X1=2|Y=1)=4/12,P(X1=3|Y=1)=5/12
P(X2=S|Y=1)=2/12,P(X2=M|Y=1)=5/12,P(X2=L|Y=1)=5/12
P(X1=1|Y=-1)=4/9,P(X1=2|Y=-1)=3/9,P(X1=3|Y=-1)=2/9
P(X2=S|Y=-1)=4/9,P(X2=M|Y=-1)=3/9,P((X2=L|Y=-1)=2/9
所以对于给定的x=(2,S)T计算:
P(Y=1)P(X1=2|Y=1)P(X2=S|Y=1)=(10/17)(4/12)(2/12)=0.0327
P(Y=-1)P(X1=2|Y=-1)P(X2=S|Y=-1)=(7/17)(3/9)(4/9)=0.0610
所以分类结果为y=-1
四、贝叶斯分类算法的优缺点
优点:
1、朴素贝叶斯模型发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率;
2、NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单;
缺点:
1、理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的(可以考虑用聚类算法先将相关性较大的属性聚类),这给NBC模型的正确分类带来了一定影响。在属性个数比较多或者属性之间相关性较大时,NBC模型的分类效率比不上决策树模型。而在属性相关性较小时,NBC模型的性能最为良好;
2、需要知道先验概率;
3、分类决策存在错误率;