数据结构课设:神秘国度的爱情故事
神秘国度的爱情故事
题目要求:某个太空神秘国度中有很多美丽的小村,从太空中可以想见,小村间有路相连,更精确一点说,任意两村之间有且仅有一条路径。小村 A 中有位年轻人爱上了自己村里的美丽姑娘。每天早晨,姑娘都会去小村 B 里的面包房工作,傍晚 6 点回到家。年轻人终于决定要向姑娘表白,他打算在小村 C 等着姑娘路过的时候把爱慕说出来。问题是,他不能确定小村 B 是否在小村 A到小村 C 之间的路径上。你可以帮他解决这个问题吗?
输入 :第一行是村庄的个数M,接下来M-1行每行两个树Va,Vb表示哪些村庄是直接相连的,之后是提问次数N,接下来N行每行3个整数va,vb,vc,每组发问若vb在va与vc的必经之路上则输出"yes",否则输出"No"
设计思想
有两个类:Create_Sample //产生样本的类,
Yes_or_NO //判对是否告白成功的类
类里面的函数,成员,和功能,都在上面的图中说明了.
下面就来说说算法设计原理:
①首先通过Create_Sample来产生测试数据,如何产生随机,不重复的,n个数呢.
思路:产生一个n大小的升序数组, 对数据中任意u,v来个数交换即可.保存在queue中
②如何产生随机,不重复的n-1条边呢.
思路:利用两个queue,来配合交互,产生,具体可看代码实现
③如何产生随机,m次正确有效询问呢.
思路:不予许错误的提问即可,如代码中,当a == b || b == c || a == c,这些无意义的提问,直接不允许就行,具体实现看代码
④接着有了数据就开始Yes_or_No了
首先,通过构造函数,来动态申请空间
接着,将边集连起来,形成一个无向图
接着,用bfs广度优先搜索预处理一下这个图,为图中的点之间形成父子关系,和深度关系,用于下一步.
(具体的父子关系,和深度关系怎么预处理请看具体代码实现,这里不加赘述)
接着,用LCA最近公关祖先算法,找到两点之间的最近公共祖先,这里用到了预处理的父子关系,和深度关系的方法来找祖先.
最后,用meeeeet函数来判断,a,b,c的点lca关系,从而得到小伙子是否可以遇见姑娘.
最后的最后,析构函数,释放空间
源程序
#include
using namespace std;
int top = 1;
char test[] = "test2222.txt";
char out[] = "out2222.txt";
class Create_Sample //产生样本的类
{
private:
queue q;
queue que;
public:
void init(int n); //产生一组1-n不重复的数
void creattree(int n);
void creatquery(int n);
};
class Yes_or_NO //判对是否告白成功的类
{
private:
struct Edge_node
{
int adjnode;
Edge_node *next;
};
struct Node
{
int id;
int fa;
int depth;
Edge_node *fristarc;
};
public:
Node *node;
Yes_or_NO(int n)
{
node = new Node[n + 1]; //动态申请n+1个结点空间
};
void creatgraph(int n);
void BFS(int root);
int LCA(int u, int v);
void meeeeet(int a, int b, int c);
~Yes_or_NO()
{
delete node;
}
};
void Create_Sample_main()
{
#ifndef BLIME
freopen(test, "w", stdout);
#endif
int T, n;
cin >> T >> n; //tests number and villages number
cout << T << endl;
Create_Sample s;
top = 0;
for (int i = 1; i <= T; i++)
{
top++;
s.init(n);
s.creattree(n);
s.creatquery(n);
}
}
void YN_main()
{
#ifndef PLS
freopen(test, "r", stdin);
freopen(out, "w", stdout);
#endif
int T, n, m;
int a, b, c;
cin >> T;
cout << "测试样例数T:\t" << T << endl;
while (T--)
{
cin >> n;
cout << "结点数n\t" << n << endl;
Yes_or_NO mg(n);
mg.creatgraph(n); //建树
mg.BFS(0); //预处理出树结点的深度和对应父亲结点
cin >> m;
cout << "m个询问:\t" << m << endl;
while (m--)
{
cin >> a >> b >> c;
mg.meeeeet(a, b, c);
}
}
}
int main()
{
clock_t stime,etime;
stime=clock();
Create_Sample_main();
YN_main();
etime=clock();
cout << "The run time is: " << (double)(etime - stime) / CLOCKS_PER_SEC << "s" << endl;
}
void Create_Sample::init(int n)
{
while (!q.empty())
q.pop(); //确保q严格为空
// int num[maxn];
// for (int i = 0; i < n; i++)
// {
// num[i] = i;
// }
int *num = new int[n];
for (int i = 0; i < n; i++)
{
num[i] = i;
}
srand(time(NULL));
for (int i = 0; i < n; i++)
{
int tmp = (rand() + top) % n;
swap(num[i], num[tmp]);
}
for (int i = 0; i < n; i++)
{
q.push(num[i]);
}
}
void Create_Sample::creattree(int n)
{
cout << n << endl;
srand(time(NULL));
int u = q.front();
q.pop();
que.push(u);
n--;
while (!que.empty())
{
u = que.front();
que.pop();
int tmp = (rand() + top) % 10;
//tmp = tmp % 2; //两种询问方式
if (tmp == 0 && que.empty())
{
tmp++;
}
for (int i = 1; i <= tmp; i++)
{
if (q.empty())
break;
int v = q.front();
q.pop();
que.push(v);
cout << u << " " << v << endl;
}
}
}
void Create_Sample::creatquery(int n)
{
srand(time(NULL));
int tmp = (rand() + top) % n + 100;
tmp = 100;
cout << tmp << endl;
for (int i = 1; i <= tmp; i++)
{
int a = (rand() + top) % n;
int b = (rand() + top) % n;
int c = (rand() + top) % n;
if (a == b || b == c || a == c)
{
i--;
continue;
}
cout << a << " " << b << " " << c << endl;
}
}
void Yes_or_NO::creatgraph(int n)
{
Edge_node *p;
int u, v;
int nodenum = n;
int edgenum = n - 1;
for (int i = 0; i < nodenum; i++) //初始化图的每个点
{
node[i].id = i;
node[i].fristarc = NULL;
}
for (int i = 1; i <= edgenum; i++) //连接图的边
{
cin >> u >> v;
p = new Edge_node;
p->adjnode = u;
p->next = node[u].fristarc; //头插法连边
node[u].fristarc = p;
p = new Edge_node;
p->adjnode = v;
p->next = node[v].fristarc; //双向边
node[v].fristarc = p;
}
}
void Yes_or_NO::BFS(int root)
{ //bfs广度优先遍历,预处理出每一个结点的深度和父亲结点
queue que;
node[root].depth = 0; //深度
node[root].fa = root; //根的父亲为自己
que.push(root);
while (!que.empty()) //bfs
{
int u = que.front();
que.pop();
Edge_node *p;
for (p = node[u].fristarc; p != NULL; p = p->next) //遍历该点连接的边,并成为他们的父亲
{
int v = p->adjnode;
if (v == node[u].fa)
continue; //因为存储的是双向边,所以防止再访问到已经访问过的父亲结点
node[v].depth = node[u].depth + 1;
node[v].fa = u;
que.push(v);
}
}
}
int Yes_or_NO::LCA(int u, int v) //最近公共结点算法,返回
{
if (node[u].depth > node[v].depth)
swap(u, v); //u为深度较小的结点,v为深度较大的结点
int hu = node[u].depth, hv = node[v].depth;
int tu = u, tv = v;
for (int det = hv - hu, i = 1; i < det; i++)
{
tv = node[tv].fa;
}
if (tu == tv)
return tu;
while (tu != tv)
{
tu = node[tu].fa;
tv = node[tv].fa;
}
return tu;
}
void Yes_or_NO::meeeeet(int a, int b, int c) //分为4种情况
{
int ab = LCA(a, b);
int ac = LCA(a, c);
int bc = LCA(b, c);
cout<<"---"< 测试数据和结果
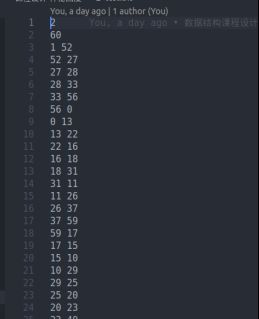
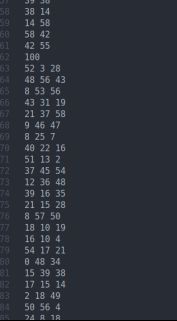
Test1:60个村庄
The run time is: 0.003154s
(解释一下:这里的2就是测试数,60,就是有60个村庄,100,就是一百次询问,代码都有说明)
Test2: 600个村庄
The run time is: 0.00702s
Test3:60000个村庄
The run time is: 0.017285s
Test4:600000个村庄
The run time is: 1.61627s
Test5:6000000个村庄
The run time is: 16.7381s
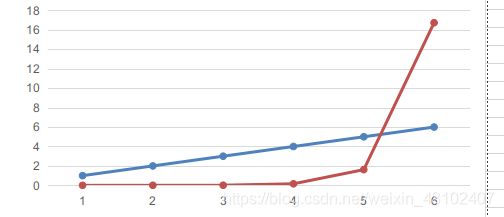
算法的时间复杂度、提出算法的改进方法
预处理时间复杂度O(nlogn),每次查询时间复杂度O(logn),总时间复杂度O(nlogn+qlogn)
算法的改进方法:
我的算法中,LCA算法用的是倍增算法,它每次查询的复杂度为O(logn),如果用Tarjan(离线)算法的话,预处理时间复杂度不变,每次查询复杂度为O(1),总时间复杂度为O(nlogn+q)
Tarjan算法大致实现过程:
先选择一个节点u为根节点,从根节点开始搜索。(标记u已访问过)
遍历该点u的所有儿子节点v,并标记v已访问过。
若v还有儿子节点,对v重复ii操作,否则进入下一操作。
把v合并到u上(并查集)。
把当前的点设为u,遍历与u有询问关系的节点v。
如果v在之前已经被访问过,那么u和v的最近公共祖先就是v通过并查集合并后的父亲节点(注意是合并后),即当前的find(v)。
Tarjan算法的伪代码:
Tarjan(u) //根节点u
{
for each(u,v)
{
Tarjan(v); //v还有儿子节点
join(u,v); //把v合并到u上
vis[v]=1; //访问标记
}
for each(u,v) //遍历与u有询问关系的节点v
{
if(vis[v])
{
ans=find(v);
}
}
}