第04篇 栈应用-01 表达式计算器
一、问题描述
输入一个表达式,如:(3.2+2.7)*2-(2.3+1.1)*2,计算出这个表达式的结果。
这个表达式被称为中缀表达式
二、涉及知识点
- 栈:https://blog.csdn.net/mail_liuxing/article/details/98505390
- 表达式。
三、表达式
我们的计算表示分为三种:前缀表达式(也叫波兰表达式)、中缀表达式、后缀表达式(也叫逆波兰表达式)。
首先需要说的是,这些表达式都是通过树的遍历方式来对应的,分别对应树的先序遍历、中序遍历、后续遍历。比如表达式构成的结构如下:
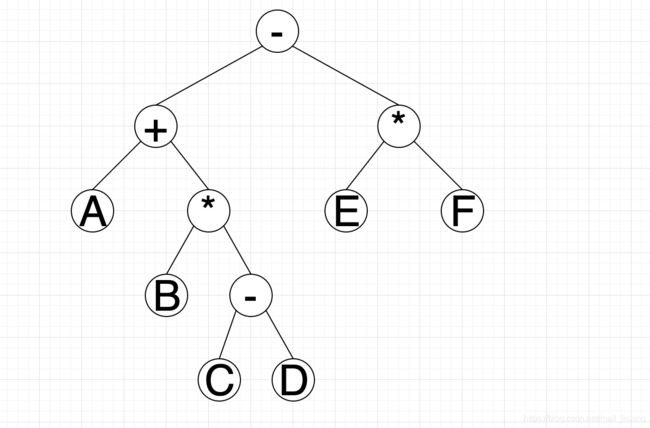
(一)中缀表达式
人类最熟悉的一种表达式1+2,(1+2)3,3+42+4等等都是中缀表示法。对于人们来说,也是最直观的一种求值方式,先算括号里的,
然后算乘除,最后算加减,对应了树的中序遍历,所以,对于上图这个树结构,中缀表达式为:A+B*(C-D)-E*F
这种表达式最为习惯,但是对于计算机运算来说,并不是很方便。
(二)前缀表达式
前缀表达式又叫做波兰式。同样的道理,表达式的前缀表达式是由相应的语法树的前序遍历的结果得到的。
如上图的前缀表达式为- + A * B - C D * E F
由前缀表达式求出结果有下面两种思路:
-
从左至右扫描表达式,如果一个操作符后面跟着两个操作数时,则计算,然后将结果作为操作数替换(这个操作符和两个操作数),
重复此步骤,直至所有操作符处理完毕。如-+AB-CDEF,扫描到-CD时,会计算C-D=C’,表达式变成:-+A*BC’*EF
继续扫描到BC’,计算BC’=B’,表达式变成:-+AB’*EF,继续+AB’,依此类推。
-
由1.知,要多遍扫描表达式,并且需要将3个字符替换成1个,比较繁锁,我们可以用一个栈S2来实现计算,扫描从右往左进行,
如果扫描到操作数,则压进S2,如果扫描到操作符,则从S2弹出两个操作数进行相应的操作,并将结果压进S2(S2的个数出2个进1个)。
当扫描结束后,S2的栈顶就是表达式结果
(三)后缀表达式
后缀表达式又叫做逆波兰式。它是由相应的语法树的后序遍历的结果得到的。如上图的后缀表达式为:
A B C D - * + E F * -
由后缀表达式求出结果十分方便,只需要用一个栈实现:
我们可以用一个栈S2来实现计算,扫描从左往右进行,如果扫描到操作数,则压进S2,如果扫描到操作符,则从S2弹出两个操作数
进行相应的操作,并将结果压进S2(S2的个数出2个进1个),当扫描结束后,S2的栈顶就是表达式结果。
后缀表达式和前缀表达式看起来就像一对逆过程,实际上并不是这样子,因为字符读取的时候都是从左往右的,所以,前缀表达式往往需要用两个栈来计算。
四、表达式的相互转换
中缀表达式转换成后缀表达式既然中缀表达式对于计算机的运算并不便利,而前缀后缀表达式的计算相对简单方便。因此,找到一种途径将中缀表达式
转换成前缀后缀表达式就十分重要。实际上,二者的转换算法看起来也很像一个逆过程。因此,我们着重讨论中缀转后缀。
(一)中缀表达式转后缀表达式
从理论上讲,已知一棵二叉树的中序遍历序列,要求出它的后序遍历序列是不唯一的,即文法是有多义性的。但是,在这里加上了优先级这一限制条件,转换就变得唯一了。
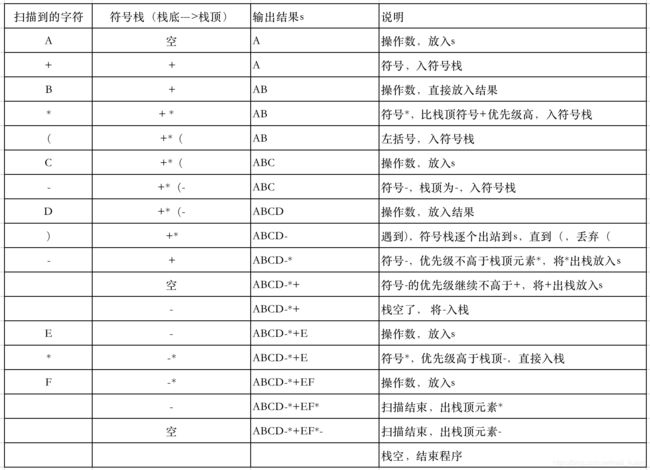
转换步骤
从左往右扫描中缀表达式串s,对于每一个操作数或操作符,执行以下操作;
- 如果扫描到的s[i]是操作数,将s[i]添加到输出字符串中;
- 如果扫描到的s[i]是左括号’(’,那么将s[i]压入栈中;
- 如果扫描到的s[i]是右括号’)’,则将栈中符号逐个出栈并添加到结果字符串s中,直到遇到左括号’(’,左括号出栈并且丢弃;
- 如果扫描到的s[i]是操作符,做如下处理:
①. 如果栈为不空 表情 栈顶不为’(’ 并且 扫描到的操作符优先级不高于栈顶操作符,那么就将栈顶字符串取出来放到结果字符串s中,再回到①;
当上面的条件不再满足,就将s[i]入栈 - 所有的都扫描完之后,将栈里面的 操作符出栈并加到输出串s中
图示
代码实现
方法名:transMidToSuffix
package com.firewolf.javabase.s004.realcase;
import static com.firewolf.javabase.s004.realcase.CalculateUtlis.isGreater;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
/**
* 后缀计算器工具,用于将中缀表达式转换成后缀表达式
*/
public class SuffixCalculatorHelper {
/**
* 把中缀表达式转换成后缀表达式,思路如下:
* 从左往右扫描中缀表达式串s,对于每一个操作数或操作符,执行以下操作;
* 1. 如果扫描到的s[i]是操作数,将s[i]添加到输出字符串中;
* 2. 如果扫描到的s[i]是左括号'(',那么将s[i]压入栈中;
* 3. 如果扫描到的s[i]是右括号')',则将栈中符号逐个出栈并添加到结果字符串s中,直到遇到左括号'(',左括号出栈并且丢弃
* 4. 如果扫描到的s[i]是操作符,做如下处理:
* ①. 如果栈为空 或者栈顶符号为'(' 或者 扫描到的操作符优先级高于栈顶操作符,那么就将操作符直接放入栈;
* ②. 如果不满足上面的条件,那么就依次将栈顶字符串取出来放到结果字符串s中,再回到①
* 当上面的条件不再满足,就将s[i]入栈
* 5. 所有的都扫描完之后,将栈里面的 操作符出栈并加到输出串s中
*/
public static String transMidToSuffix(String midExpression) {
//先把操作数和操作符以及()用集合放起来,操作起来更方便
List strings = transExpressionToList(midExpression);
int index = 0;
StringBuffer result = new StringBuffer();
Stack opStack = new Stack<>();
while (index < strings.size()) {
String s = strings.get(index);
//判断当前拿到的是数字还是操作符
if (isOperData(s)) {
//如果是数字,直接放到结果里面
putToResult(result,s);
} else if ("(".equals(s)) {
opStack.push(s);
} else if (")".equals(s)) {//右括号
String top = "";
while (!"(".equals((top = opStack.pop()))) {
putToResult(result,top);
}
} else { //操作符
while (!opStack.isEmpty() && !"(".equals(opStack.peek()) && !isGreater(s.charAt(0), opStack.peek().charAt(0))) {
putToResult(result,opStack.pop());
}
opStack.push(s);
}
index++;
}
while (!opStack.isEmpty()) {
putToResult(result,opStack.pop());
}
return result.toString();
}
/**
* 把s放到结果result中
* @param result
* @param s
*/
private static void putToResult(StringBuffer result,String s){
result.append(s).append(" ");
}
/**
* 表达式中各个数字或者符号存放到ArrayList,空格是分隔符
* @param expression 要被存储的表达式
* @return
*/
public static List transExpressionToList(String expression) {
return transExpressionToList(expression, ' ');
}
/**
*
* 表达式中各个操作数或者符号存放到ArrayList,自己指定分隔符
* @param expression 要被存储的表达式
* @param split 分隔符,各个字符之间的分隔符,如A * (B+C) 这里面的空格
* @return
*/
public static List transExpressionToList(String expression, char split) {
int index = 0;
String num = "";
List resultList = new ArrayList<>();
while (index < expression.length()) {
char c = expression.charAt(index);
if (isOperDataChar(c)) {
num = num + c;
if ((index == expression.length() - 1) || !isOperDataChar(expression.charAt(index + 1))) {
resultList.add(num);
num = "";
}
} else {
if (c != split) {
resultList.add(c + "");
}
}
index++;
}
return resultList;
}
//非数字符号
private static List notData;
static {
notData = Arrays.asList(new Character[]{'+', '-', '*', '/', '(', ')', ' '});
}
/**
* 判断是不是操作数,如果不是加减乘除和括号,就算操作数
* @return
*/
public static boolean isOperData(String string) {
for (char c : notData) {
if (string.contains(c + "")) {
return false;
}
}
return true;
}
/**
* 判断字符c是否是操作数里面的字符,如3,4等,如果表达式是A+B这种,那么A和B也是操作数里面的字符,
* 总之,不能是notData里面的元素
* @param c
* @return
*/
private static boolean isOperDataChar(char c) {
return !notData.contains(c);
}
}
其中:CalculateUtlis.isGreater 方法用于判断操作符的优先级,除此之外,CalculateUtlis还有一些方法,如:判断您是否是数字等,用于后面的计算器实现,代码内容如下:
CalculateUtlis:
package com.firewolf.javabase.s004.realcase;
import java.util.HashMap;
import java.util.Map;
public class CalculateUtlis {
private static Map opPriority ;
static {
opPriority = new HashMap<>();
opPriority.put('+',1);
opPriority.put('-',1);
opPriority.put('*',2);
opPriority.put('/',2);
}
/**
* 判断字符c是否是数字
* @param c
* @return
*/
public static boolean isDigitChar(char c){
return c >= '0' && c<='9';
}
/**
* 判断字符c是不是数字或者是逗号
* @param c
* @return
*/
public static boolean isDigitCharOrComma(char c){
return c >= '0' && c<='9' || c=='.';
}
/**
* 小数运算
* @param num1
* @param num2
* @param op
* @return
*/
public static double calcute(double num1, double num2, char op) {
//这种计算方式会丢失精度
// switch (op){
// case '+':
// return num1+num2;
// case '-':
// return num1-num2;
// case '*':
// return num1*num2;
// case '/':
// return num1/num2;
// default:
// throw new RuntimeException("你的操作符不支持"+op);
// }
BigDecimal b1 = new BigDecimal(num1 + "");
BigDecimal b2 = new BigDecimal(num2 + "");
switch (op) {
case '+':
return b1.add(b2).doubleValue();
case '-':
return b1.subtract(b2).doubleValue();
case '*':
return b1.multiply(b2).doubleValue();
case '/':
return b1.divide(b2, 2, RoundingMode.HALF_UP).doubleValue();
default:
throw new RuntimeException("你的操作符不支持" + op);
}
}
/**
* 整数运算
* @param num1
* @param num2
* @param op
* @return
*/
public static int calcute(int num1, int num2, char op) {
switch (op){
case '+':
return num1+num2;
case '-':
return num1-num2;
case '*':
return num1*num2;
case '/':
return num1/num2;
default:
throw new RuntimeException("你的操作符不支持"+op);
}
}
/**
* 判断操作符op1的优先级是否大于op2
* @param op1 第一个操作符
* @param op2 第二个操作符
* @return 如果满足条件,返回true,否则返回false
*/
public static boolean isGreater(char op1, char op2) {
return opPriority.get(op1) > opPriority.get(op2);
}
}
(二)中缀表达式转前缀表达式
中缀表达式转换成前缀表达式和中缀表达式转换成后缀表达式十分类似,只需要将扫描方向由前往后变成由后往前,将’(‘改为’)’,’)‘改为’(’。
五、中缀表达式计算器
(一)思路分析
这里从简单的到复杂的进行分析。
10以内没有括号的加减乘除:in10NoBrackets
这是最简单的情况,所有的运算数都是不超过10的整数,如:3+4*5-8/3*5
- 定义两个栈,一个用来存放数字,一个用来存放操作符号;
- 通过一个索引index对表达式expression进行扫描,一直到结尾;
- 如果遇到数字,就直接入数字栈;
- 如果遇到的是符号,则分如下情况处理:
①. 符号栈没有符号,则直接入符号站;
②. 符号站有符号,则比较当前符号和符号栈的符号的优先级,如果当前的优先,则直接入栈;否则,弹出符号栈的符号,并从数字栈弹出两个数字进行计算,结果存入数字栈,并且把当前操作符入符号栈
③. 当表达式扫描完之后,就循环的从数字栈取出两个数子、从符号栈弹出一个符号,进行运算,将结果再压入数字栈,直到符号栈为空;
④. 最终留在数字栈的就是计算的结果
没有括号的加减乘除:noBrackets
第一种情况是对每个字符进行判断是不是数字,不能计算2位及以上的表达式,需要能够处理2位及以上整数的加减乘除,如:3+4*53-82/3*12。
- 定义一个tmp用来缓存遍历到的数字;
- 如果检测到了数字,那么就拼接到tmp的后面,再判断下一个字符的情况:
如果下一个字符没有了,也就是说当前的指针index==expression.length()-1,那么直接把tmp转成数字压入数字栈;
如果下一个是运算符,那么也需要把tmp压入数字栈,并清空tmp,用于缓存下一个数字;
带有括号的加减乘除:brackets
需要添加带有括号的运算实现,如:((3+4)*3-5)*4-(4-2)*5
- 如果遇到’(’,直接入栈;
- 如果遇到’)’,就循环从数字站弹出两个数字,从符号栈弹出一个符号,进行计算,并将计算的结果放入数字栈,直到从符号栈取出来的是’(’;
浮点数的加减乘除:decimals
还需要支持带有小数的运算,如:(3.2+2.7)*2-(2.3+1.1)*2
- 我们只需要在判断是否是数字的时候,认为. 也是数字即可。
(二)代码实现
package com.firewolf.javabase.s004.realcase;
import java.util.Stack;
import static com.firewolf.javabase.s004.realcase.CalculateUtlis.*;
/**
* 中缀表达式计算器
*/
public class MidCalculator {
/**
* 10以内没有括号的加减乘除算法
* 实现思路:
* 1. 定义两个栈,一个用来存放数字,一个用来存放操作符号;
* 2. 通过一个索引index对表达式expression进行扫描,一直到结尾;
* 3. 如果遇到数字,就直接入数字栈;
* 4. 如果遇到的是符号,则分如下情况处理:
* ①. 符号栈没有符号,则直接入符号站;
* ②. 符号站有符号,则比较当前符号和符号栈的符号的优先级,如果当前的优先,则直接入栈;
* 否则,弹出符号栈的符号,并从数字栈弹出两个数字进行计算,结果存入数字栈,并且把当前操作符入符号栈
* ③. 当表达式扫描完之后,就顺序的从数字栈和符号栈弹出数字和符号进行运算,将结果再压入数字栈,直到符号栈为空;
* ④. 最终留在数字栈的就是计算的结果
*/
public static int in10NoBrackets(String expression) {
Stack numStack = new Stack<>();
Stack opStack = new Stack<>();
int index = 0;
while (index < expression.length()) {
char c = expression.charAt(index);
if (isDigitChar(c)) { //表明是数字
numStack.push(c - 48);
} else {
if (opStack.isEmpty()) {
opStack.push(c);
} else {
char top = opStack.peek();
if (isGreater(c, top)) {//当前操作符比栈顶操作符优先级高,直接入栈
opStack.push(c);
} else {
//进行计算
char op = opStack.pop();
int num2 = numStack.pop(); //这个先弹出来,
int num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
int result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
//将现在扫描到的符号入符号栈
opStack.push(c);
}
}
}
index++; //移动下标
}
int result = 0;
while (!opStack.isEmpty()) {
char op = opStack.pop();
int num2 = numStack.pop(); //这个先弹出来,
int num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
}
return numStack.pop();
}
/**
* 没有括号的计算
* 基本思路和10以内的一样,不同的是,不是每个字符都入栈,如果是数字字符的话,需要通过一个变量来记录到整个数字,直到下一个是符号为止;
* @param expression
* @return
*/
public static int noBrackets(String expression) {
Stack numStack = new Stack<>();
Stack opStack = new Stack<>();
int index = 0;
String tmp = "";
while (index < expression.length()) {
char c = expression.charAt(index);
if (isDigitChar(c)) { //表明是数字
tmp = tmp + c; //缓存数字
//判断下一个是不是数字,如果不是字符,就表示数字结束了,需要把数字入栈;
if (index == expression.length() - 1
|| !isDigitChar(expression.charAt(index + 1))) {
numStack.push(Integer.parseInt(tmp));
tmp = "";//清空
}
} else {
if (opStack.isEmpty()) {
opStack.push(c);
} else {
char top = opStack.peek();
if (isGreater(c, top)) {//当前操作符比栈顶操作符优先级高,直接入栈
opStack.push(c);
} else {
//进行计算
char op = opStack.pop();
int num2 = numStack.pop(); //这个先弹出来,
int num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
int result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
//将现在扫描到的符号入符号栈
opStack.push(c);
}
}
}
index++; //移动下标
}
int result = 0;
while (!opStack.isEmpty()) {
char op = opStack.pop();
int num2 = numStack.pop(); //这个先弹出来,
int num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
}
return numStack.pop();
}
/**
* 带有括号的运算
* 在简单的运算基础上,添加如下处理:
* 1. 如果遇到'(',直接入栈;
* 2. 如果遇到')',就循环如下操作:
* 从数字站弹出两个数字,从符号栈弹出一个符号,进行计算,并将计算的结果放入数字栈
* 直到从符号栈取出来的是'('
* @param expression
* @return
*/
public static int brackets(String expression) {
Stack numStack = new Stack<>();
Stack opStack = new Stack<>();
int index = 0;
String tmp = "";
while (index < expression.length()) {
char c = expression.charAt(index);
if (isDigitChar(c)) { //表明是数字
tmp = tmp + c; //缓存数字
//判断下一个是不是数字,如果不是字符,就表示数字结束了,需要把数字入栈;
if (index == expression.length() - 1
|| !isDigitChar(expression.charAt(index + 1))) {
numStack.push(Integer.parseInt(tmp));
tmp = "";//清空
}
} else if (c == '(') {//处理左括号
opStack.push('(');
} else if (c == ')') { //处理右括号
char fuhao;
while ((fuhao = opStack.pop()) != '(') {
int num2 = numStack.pop(); //这个先弹出来,
int num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
int result = calcute(num1, num2, fuhao);
//将结果入数字栈
numStack.push(result);
}
} else {
if (opStack.isEmpty()) {
opStack.push(c);
} else if (opStack.peek() == '(') {
opStack.push(c);
} else {
char top = opStack.peek();
if (isGreater(c, top)) {//当前操作符比栈顶操作符优先级高,直接入栈
opStack.push(c);
} else {
//进行计算
char op = opStack.pop();
int num2 = numStack.pop(); //这个先弹出来,
int num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
int result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
//将现在扫描到的符号入符号栈
opStack.push(c);
}
}
}
index++; //移动下标
}
int result = 0;
while (!opStack.isEmpty()) {
char op = opStack.pop();
int num2 = numStack.pop(); //这个先弹出来,
int num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
}
return numStack.pop();
}
/**
* 带有小数的计算,思路几乎没有任何变化, 只需要在遇到.的时候,把它当做数字存放在数字缓存中即可
* 注意的是,这个保证不了精度
* @param expression
* @return
*/
public static double decimals(String expression) {
Stack numStack = new Stack<>();
Stack opStack = new Stack<>();
int index = 0;
String tmp = "";
while (index < expression.length()) {
char c = expression.charAt(index);
if (isDigitCharOrComma(c)) { //表明是数字,如果是.,也认为是数字的一部分
tmp = tmp + c; //缓存数字
//判断下一个是不是数字,如果不是字符,就表示数字结束了,需要把数字入栈;
if (index == expression.length() - 1
|| !isDigitCharOrComma(expression.charAt(index + 1))) {
numStack.push(Double.parseDouble(tmp));
tmp = "";//清空
}
} else if (c == '(') {//处理左括号
opStack.push('(');
} else if (c == ')') { //处理右括号
char fuhao;
while ((fuhao = opStack.pop()) != '(') {
double num2 = numStack.pop(); //这个先弹出来,
double num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
double result = calcute(num1, num2, fuhao);
//将结果入数字栈
numStack.push(result);
}
} else {
if (opStack.isEmpty()) {
opStack.push(c);
} else if (opStack.peek() == '(') {
opStack.push(c);
} else {
char top = opStack.peek();
if (isGreater(c, top)) {//当前操作符比栈顶操作符优先级高,直接入栈
opStack.push(c);
} else {
//进行计算
char op = opStack.pop();
double num2 = numStack.pop(); //这个先弹出来,
double num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
double result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
//将现在扫描到的符号入符号栈
opStack.push(c);
}
}
}
index++; //移动下标
}
double result = 0;
while (!opStack.isEmpty()) {
char op = opStack.pop();
double num2 = numStack.pop(); //这个先弹出来,
double num1 = numStack.pop(); //这个后弹出来,正常应该是num1在前,如num1-num2,而不应该是num2-num1
result = calcute(num1, num2, op);
//将结果入数字栈
numStack.push(result);
}
return numStack.pop();
}
}
六、后缀表达式计算器
(一)思路分析
扫描后缀表达式:
- 遇到操作数的时候,直接入栈;
- 遇到操作符号的时候,从栈顶弹出两个数据,计算结果,
- 直到扫描完表达式,那么栈中的元素就是结果
(二)代码实现
package com.firewolf.javabase.s004.realcase;
import java.util.Stack;
import static com.firewolf.javabase.s004.realcase.CalculateUtlis.calcute;
/**
* 后缀表达式计算器
*/
public class SuffixCalculator {
/**
* 通过后缀表达式的方式计算中缀表达式的值,
* 扫描表达式:
* 1. 遇到操作数的时候,直接入栈;
* 2. 遇到操作符号的时候,从栈顶弹出两个数据,计算结果,
* 直到扫描完表达式,那么栈中的元素就是结果
* @param expression
* @return
*/
public static double calculate(String expression) {
String suffixExpression = SuffixCalculatorHelper.transMidToSuffix(expression);
String[] allStr = suffixExpression.split(" ");
Stack numStack = new Stack<>();
for (String s : allStr) {
if (SuffixCalculatorHelper.isOperData(s)) {
numStack.push(Double.parseDouble(s));
} else {
double num2 = numStack.pop();
double num1 = numStack.pop();
double result = calcute(num1, num2, s.charAt(0));
numStack.push(result);
}
}
return numStack.pop();
}
}