【SPOJ2916 GSS5】Can you answer these queries V——杨子曰题目
【SPOJ GSS5】Can you answer these queries V——杨子曰题目
题目描述
You are given a sequence A[1], A[2], …, A[N] . ( |A[i]| <= 10000 , 1 <= N <= 10000 ). A query is defined as follows: Query(x1,y1,x2,y2) = Max { A[i]+A[i+1]+…+A[j] ; x1 <= i <= y1 , x2 <= j <= y2 and x1 <= x2 , y1 <= y2 }. Given M queries (1 <= M <= 10000), your program must output the results of these queries.
输入格式:
The first line of the input consist of the number of tests cases <= 5. Each case consist of the integer N and the sequence A. Then the integer M. M lines follow, contains 4 numbers x1, y1, x2 y2.
输出格式:
Your program should output the results of the M queries for each test case, one query per line.
输入样例:
2
6 3 -2 1 -4 5 2
2
1 1 2 3
1 3 2 5
1 1
1
1 1 1 1
输出样例:
2
3
1
一道毒瘤数据结构题:给你一个序列,对于每一个询问的 l 1 , r 1 , l 2 , r 2 l_1,r_1,l_2,r_2 l1,r1,l2,r2,输出左端点在 [ l 1 , r 1 ] [l_1,r_1] [l1,r1],右端点在 [ l 2 , r 2 ] [l_2,r_2] [l2,r2]的子段中最大的和
请先用线段树解决这道题:【SPOJ GSS3】Can you answer these queries III
假设你已经看了上面那篇题解,我们来讲一讲这道题的思路:
首先我们在线段树上要维护的东西和上面那道题是完全一样的,在这里罗列一下:
- ms:给区间的最大字序列和
- ls:包括左端点的区间最大子序列和
- rs:包括右端点的区间最大子序列和
- sum:区间的和
显然要分类讨论了,那我们就来讨论一下(下文的区间[l,r]的端点不一定是准确的,在代码中需要+1或者-1,保证在临界位置不会重复计算):
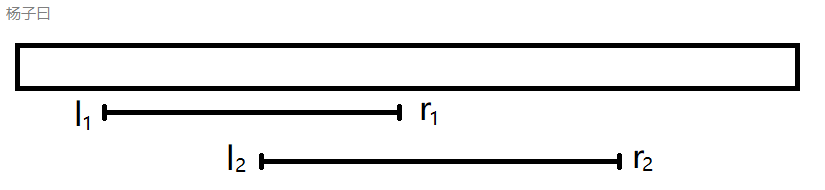
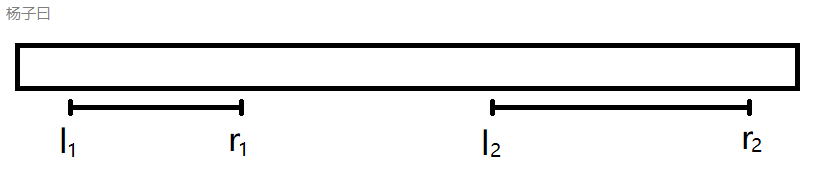
首先,两个区间不相交:
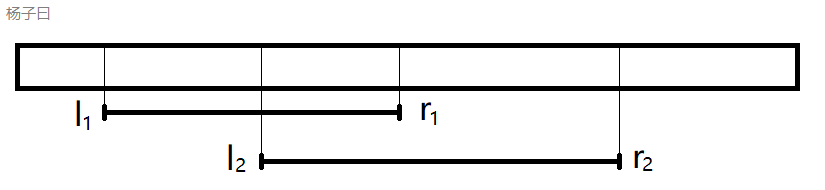
然后你有没有发现满足要去的子序列一定包含中间这一段:
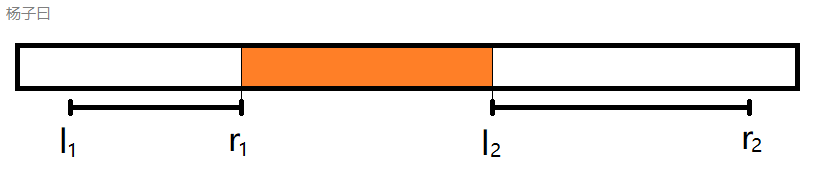
So,我们要把区间 ( r 1 , l 2 ) (r_1,l_2) (r1,l2)这一段的sum求出来,然后我们还要考虑两边,比如答案长这样:

那么蓝色和绿色分别是神马捏?应该就是区间 [ l 1 , r 1 ] [l_1,r_1] [l1,r1]的rs和区间 [ l 2 , r 2 ] [l_2,r_2] [l2,r2]的ls,OK,第一种情况就被我们解决了
-
答案横跨了一段(只能是中间那一段)

这很简单,就是区间 [ l 2 , r 1 ] [l_2,r_1] [l2,r1]的ms -
答案横跨两段(以靠左边为例)
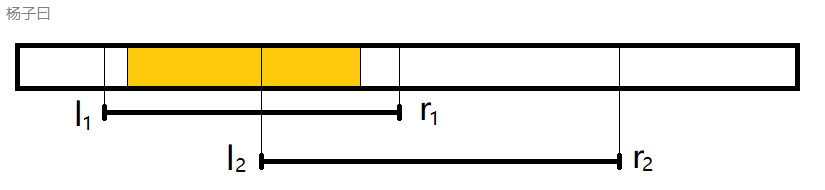
这个是什么呢?
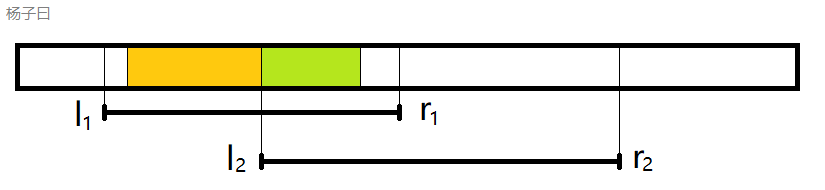
有没有发现黄色是区间 [ l 1 , l 2 ] [l_1,l_2] [l1,l2]的rs,而绿色部分则是区间 ( l 2 , r 1 ] ( 就 是 [ l 2 + 1 , r 1 ] ) (l_2,r_1](就是[l_2+1,r_1]) (l2,r1](就是[l2+1,r1])的ls
如果区间靠右边也是一样的 -
答案横跨3个区间
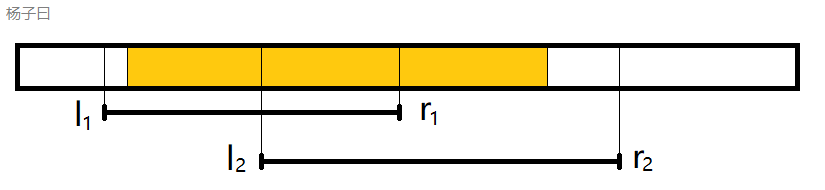
这可以怎么算捏?
很多人可能会想到分成3段来算
但其实我们只要这样就可以了:
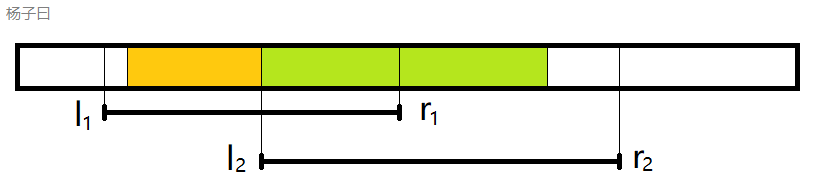
黄色是区间 [ l 1 , l 2 ] [l_1,l_2] [l1,l2]的rs,而绿色部分则是区间 ( l 2 , r 2 ] ( 就 是 [ l 2 + 1 , r 2 ] ) (l_2,r_2](就是[l_2+1,r_2]) (l2,r2](就是[l2+1,r2])的ls
然后机智的你一定发现了第2种情况是可以这种情况何在一起算的,就是 [ l 1 , l 2 ] 的 r s + 区 间 ( l 2 , r 2 ] 的 l s [l_1,l_2]的rs+区间(l_2,r_2]的ls [l1,l2]的rs+区间(l2,r2]的ls
至此我们终于把所有的情况全部讨论完了
OK,完事
C++代码:
#include参考:
https://www.luogu.org/blog/energy2002/solution-sp2916
于HG机房