蓝桥杯：贪心算法例子java实现
什么是贪心算法呢？所谓贪心算法是指，在对问题求解时，总是做出在当前看来最好的选择。也就是说，不从整体最优解出发来考虑，它所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题都能产生整体最优解或整体最优解的近似解。
贪心算法的基本思路如下：
1.建立数学模型来描述问题。
2.把求解的问题分成若干个子问题。
3.对每个子问题求解，得到每个子问题的局部最优解。
4.把每个子问题的局部最优解合成为原来问题的一个解。
实现该算法的过程：
从问题的某一初始状态出发；
while 能朝给定总目标前进一步 do
求出可行解的一个解元素；
由所有解元素组合成问题的一个可行解。
利用贪心算法解题，需要解决两个问题：
一是问题是否适合用贪心法求解。我们看一个找币的例子，如果一个货币系统有三种币值，面值分别为一角、五分和一分，求最小找币数时，可以用贪心法求解；如果将这三种币值改为一角一分、五分和一分，就不能使用贪心法求解。用贪心法解题很方便，但它的适用范围很小，判断一个问题是否适合用贪心法求解，目前还没有一个通用的方法，在信息学竞赛中，需要凭个人的经验来判断。
二是确定了可以用贪心算法之后，如何选择一个贪心标准，才能保证得到问题的最优解。在选择贪心标准时，我们要对所选的贪心标准进行验证才能使用，不要被表面上看似正确的贪心标准所迷惑，
区间相关问题：
1.选择不相交的区间：数轴上有n个开区间（begin，end），尽量选择多个区间，使得这些区间两两没有公共点。
贪心策略：按照 end从小到大的顺序黑区间排序，取第一个区间
2.区间选点问题：数轴上有n个闭区间[ai,bi]，取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）。
贪心策略：按照b从小到大的顺序将区间排序（b相同时，a从大到小排序），则如果出现区间包含的情况，小区间一定排在前面。第一个区间取最后一个点。
例子：合理分配
某君生活的国度，经过一场大战之后，建立了一个新的国度。国王打算让那些将军们，每人选择一个自己喜欢的区间段（这些将军们守卫的地方类似中国的古长城，是一条线段）去守卫他的国家。
为了使最多的将军能守卫自己想守卫的地方，怎么的安排是最合理的呢？
长城的区间段是[1,1000]。任意两个将军守卫的地方不能有重合的地方，否则会出现争执。两个点之间的交集不算交集。
例如 1 2 和2 3 是没有交集的。
但是1 3 和 2 4 是有交集，是会产生冲突的。
下面是每位将军期望守卫的区间段。
2 324
320 424
259 342
371 888
264 634
909 982
117 653
677 929
656 707
297 915
904 943
309 564
564 601
675 876
33 89
363 912
226 952
86 129
216 339
258 857package 蓝桥杯2018年B组第三次模拟赛;
import java.util.Arrays;
import java.util.Scanner;
public class 合理分配 {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scan=new Scanner(System.in);
ChangCheng[] ccs=new ChangCheng[20];
for(int i=0;i<20;i++){
ccs[i]=new ChangCheng(scan.nextInt(),scan.nextInt());
}
Arrays.sort(ccs);
int count=1;
int nowEnd=ccs[0].end;
System.out.println("第1个区间为："+ccs[0].begin+","+ccs[0].end);
for(int i=1;i<20;i++){
if(ccs[i].begin>=nowEnd){
count++;
System.out.println("第"+count+"个区间为："+ccs[i].begin+","+ccs[i].end);
nowEnd=ccs[i].end;
}
}
System.out.println(count);
}
}
class ChangCheng implements Comparable{
int begin;
int end;
public int getBegin() {
return begin;
}
public void setBegin(int begin) {
this.begin = begin;
}
public int getEnd() {
return end;
}
public void setEnd(int end) {
this.end = end;
}
@Override
/*public String toString()返回该对象的字符串表示。通常，toString 方法会返回一个“以文本方式表示”此对象的字符串。结果应是一个简明但易于读懂的信息表达式。建议所有子类都重写此方法。Object类的 toString 方法返回一个字符串，该字符串由类名（对象是该类的一个实例）、at标记符“@”和此对象哈希码的无符号十六进制表示组成。换句话说，该方法返回一个字符串，它的值等于：
getClass().getName() + '@' + Integer.toHexString(hashCode())
返回：该对象的字符串表示形式。*/
public String toString() {
return "ChangCheng [begin=" + begin + ", end=" + end + "]";
}
public ChangCheng(int begin, int end) {
super();
this.begin = begin;
this.end = end;
}
public ChangCheng() {
super();
// TODO Auto-generated constructor stub
}
@Override
//使用Comparable接口中的compareTo方法使原本无法比较的对象通过某种自身条件来排序.（升序）
public int compareTo(ChangCheng cc) {
if(this.end>cc.end){
return 1;
}
else if(this.end 输出结果：
第1个区间为：33,89
第2个区间为：216,339
第3个区间为：564,601
第4个区间为：656,707
第5个区间为：904,943
5
背包相关问题：
1.最优装载问题：给出n个物体，第i个重量为wi，选择尽量多的物体，使其总重量不超过C.
贪心策略：将重量从小到大排序，一次选择每个物品，直到装不下为止。
2.部分背包问题：有n个物体，第i个重量为wi，价值为vi。在总重量不超过C的情况下使其总价值最高。每一个物体可以只取走一部分，价值和重量按比例来计算。
贪心策略：优先拿"价值除以重量的值"最大的，直到重量和为C。（注意：因为每个物体可以只取走一部分，因此一定可以让总重量恰好为C，或者全部拿走都不足C,而且除了最后一个以外，所有的物品要么不拿，要么拿走全部）
3.乘船问题：有n个人，第i个人重量为wi。每艘船最大载重量为C，且最多只能乘坐两个人。要求用最少的穿装载所有人。
贪心策略：体重按照从小到大排序，如果最轻的人和次轻的人都无法同船，那么只能每人一艘船；否则，他应该和他体重加起来不超过C的人中最重的人同船。
例子：生日购物
今天小红生日，小明打算给小红买些礼物。小明十分清楚小红的喜好，知道小红对每种物品的喜好程度。市场上有 20 种物品是小红喜欢的，小明虽然想把这 20 种物品全部购买，但是书包容量只有 500 。小明在想怎么买东西能让小红最开心呢（每种物品只能购买一次，所购买的物品空间总和不能超过背包容量）？下面是每种物品所占用的空间，和小红的喜欢程度。
2 1
10 5
22 5
23 5
23 4
32 5
13 2
35 5
21 3
22 3
25 3
35 3
64 5
34 2
85 5
88 4
85 3
82 2
76 1
98 1
package 蓝桥杯2018年B组第三次模拟赛;
import java.util.Arrays;
import java.util.Scanner;
public class 生日购物 {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
//贪心算法，将喜欢程度/所占空间的比值进行从大到小排序
//或者说是将所占空间/喜欢程序的比值进行从大到小排序
Scanner scan=new Scanner(System.in);
int[][] arr=new int[20][2];
for(int i=0;i<20;i++){
for(int j=0;j<2;j++){
arr[i][j]=scan.nextInt();
}
}
Flower[] fs=new Flower[20];
for(int i=0;i<20;i++){
fs[i]=new Flower(arr[i][0],arr[i][1]);
}
Arrays.sort(fs);
for(int i=0;i<20;i++){
System.out.println(fs[i]);
}
int sum=0;//占用空间
int xihao=0;//总喜好值
for(int i=0;i<20;i++){
sum+=fs[i].getKongjian();
if(sum<500){
xihao+=fs[i].getXihao();
//System.out.println(fs[i].getKongjian());
}
else{
sum-=fs[i].getKongjian();
xihao+=((500-sum)*1.0/fs[i].kongjian)*fs[i].getXihao();//最后一种花不能全部买完，就买了部分（按照题目正确答案的意思）将500空间全部用完
break;
}
}
System.out.println(xihao);
}
}
class Flower implements Comparable{
int kongjian;
int xihao;
public int getKongjian() {
return kongjian;
}
public void setKongjian(int kongjian) {
this.kongjian = kongjian;
}
public int getXihao() {
return xihao;
}
public void setXihao(int xihao) {
this.xihao = xihao;
}
public Flower() {
super();
// TODO Auto-generated constructor stub
}
public Flower(int kongjian, int xihao) {
super();
this.kongjian = kongjian;
this.xihao = xihao;
}
@Override
public String toString() {
return "Flower [kongjian=" + kongjian + ", xihao=" + xihao + "]";
}
@Override
public int compareTo(Flower f) {
if(this.kongjian*1.0/this.xihao>f.kongjian*1.0/f.xihao){
return 1;
}else if(this.kongjian*1.0/this.xihao==f.kongjian*1.0/f.xihao){
return 0;
}else{
return -1;
}
}
} 输出结果：
Flower [kongjian=2, xihao=1]
Flower [kongjian=10, xihao=5]
Flower [kongjian=22, xihao=5]
Flower [kongjian=23, xihao=5]
Flower [kongjian=23, xihao=4]
Flower [kongjian=32, xihao=5]
Flower [kongjian=13, xihao=2]
Flower [kongjian=35, xihao=5]
Flower [kongjian=21, xihao=3]
Flower [kongjian=22, xihao=3]
Flower [kongjian=25, xihao=3]
Flower [kongjian=35, xihao=3]
Flower [kongjian=64, xihao=5]
Flower [kongjian=34, xihao=2]
Flower [kongjian=85, xihao=5]
Flower [kongjian=88, xihao=4]
Flower [kongjian=85, xihao=3]
Flower [kongjian=82, xihao=2]
Flower [kongjian=76, xihao=1]
Flower [kongjian=98, xihao=1]
58
凑钱
某国度，有各种面值的钱币。现在某君手上有 30枚硬币，他们的面额分别是：
1 4 3 4 8 8 4 2 5 1 405 363 197 470 59 121 443 329 111 93 63 16 290 367 154 192 98 234 163 434
请问某君凑不出最小的金额是多少？
贪心策略：将其进行排序（升序），然后利用贪心的思想，每次都取所能取到的最大值，倒序进行取，直到取到第一个元素最小的值以后还不能使其凑够，就证明已经凑不出了。
package 蓝桥杯2018年B组第四次模拟赛;
import java.util.Arrays;
import java.util.Scanner;
public class 凑钱 {
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
int[] arr=new int[30];
for(int i=0;i<30;i++){
arr[i]=scan.nextInt();
}
Arrays.sort(arr);//升序排序
for(int i=0;i=0;j--){
if(arr[j]<=sum){
sum=sum-arr[j];//倒序进行相减，只有能够减为0才证明能够凑齐，也不需要在倒序减前面的数了
if(sum==0){
//System.out.println(i);
break;
}
}
}
if(j==-1){ //如果倒序的数值都减完了还不能使其减为0，则说明这个i值是凑不出来的。
System.out.println(i);
break;
}
}
}
} 输出结果：
1 1 2 3 4 4 4 5 8 8 16 59 63 93 98 111 121 154 163 192 197 234 290 329 363 367 405 434 443 470
57
Huffman编码：
最优编码问题：给n个字符的频率才，给每个字符赋予一个01编码串，使得任意一个字符的编码不是另外一个的前缀，而且编码后的总长度（字符的频率与编码长度乘积的总和）尽量小。
贪心策略：要生成这种编码，最方便的就是用二叉树，把要编码的字符放在二叉树的叶子上，所有的左节点是0，右节点是1，从根浏览到叶子上，因为字符只能出现在树叶上，任何一个字符的路径都不会是另一字符路径的前缀路径，符合前缀原则编码就可以得到。
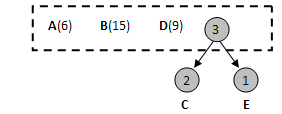
现在我们可以开始考虑压缩的问题，如果有一篇只包含这五个字符的文章，而这几个字符的出现的次数如下：
A: 6次
B : 15次
C: 2次
D : 9次
E: 1次
哈夫曼算法的步骤是这样的：
- 从各个节点中找出最小的两个节点，给它们建一个父节点，值为这两个节点之和。
- 然后从节点序列中去除这两个节点，加入它们的父节点到序列中。
- 重复上面两个步骤，直到节点序列中只剩下唯一一个节点。这时一棵最优二叉树就已经建成了，它的根就是剩下的这个节点。
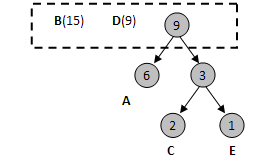
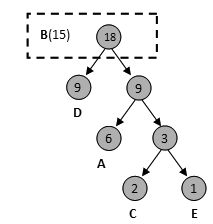
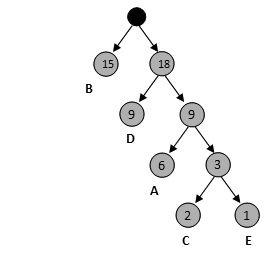
比如上面的例子，哈弗曼树建立的过程如下:
1) 列出原始的节点数据：
2) 将最小的两个节点C和E结合起来：
3) 再将新的节点和A组合起来
4) 再将D节点加入
5) 如此循环，最终得到一个最优二叉树
生成的数据文件长度为: 3*6 + 1*15 + 4*2 + 2*9 + 4*1 = 63
对于各种不同的节点序列，用哈弗曼算法建立起来的树总是一棵最优二叉树
其他问题：具体分析
［均分纸牌］有N堆纸牌，编号分别为1，2，…，n。每堆上有若干张,但纸牌总数必为n的倍数.可以在任一堆上取若干张纸牌,然后移动。移牌的规则为：在编号为1上取的纸牌，只能移到编号为2的堆上；在编号为n的堆上取的纸牌，只能移到编号为n-1的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。例如：n=4，4堆纸牌分别为：①9 ② 8 ③ 17 ④ 6 移动三次可以达到目的：从③取4张牌放到④ 再从③区3张放到②然后从②去1张放到①。
输入输出样例：4
9 8 17 6
屏幕显示：3
算法分析：设a[i]为第I堆纸牌的张数（0<=I<=n），v为均分后每堆纸牌的张数，s为最小移动次数。
我们用贪心算法，按照从左到右的顺序移动纸牌。如第I堆的纸牌数不等于平均值，则移动一次（即s加1），分两种情况移动：
1．若a[i]>v，则将a[i]-v张从第I堆移动到第I+1堆；
2．若a[i] 为了设计的方便，我们把这两种情况统一看作是将a[i]-v从第I堆移动到第I+1堆，移动后有a[i]=v; a[I+1]=a[I+1]+a[i]-v. 在从第I+1堆取出纸牌补充第I堆的过程中可能回出现第I+1堆的纸牌小于零的情况。 如n=3，三堆指派数为1 2 27 ，这时v=10，为了使第一堆为10，要从第二堆移9张到第一堆，而第二堆只有2张可以移，这是不是意味着刚才使用贪心法是错误的呢？ 我们继续按规则分析移牌过程，从第二堆移出9张到第一堆后，第一堆有10张，第二堆剩下-7张，在从第三堆移动17张到第二堆，刚好三堆纸牌都是10，最后结果是对的，我们在移动过程中，只是改变了移动的顺序，而移动次数不便，因此此题使用贪心法可行的。 贪心算法所作的选择可以依赖于以往所作过的选择，但决不依赖于将来的选择，也不依赖于子问题的解，因此贪心算法与其他算法相比具有一定的速度优势。如果一个问题可以同时用几种方法解决，贪心算法应该是最好的选择之一。public class Greedy {
public static void main(String[] args) {
int n = 0, avg =0, s = 0;
Scanner scanner = new Scanner(System.in);
ArrayList