多臂赌博机Multi-Armed Bandit(MAB)

1.问题来源：多臂赌博机问题

一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？

1）有K台机器，每次选取其中一台拉动杠杆，该机器提供一个随机的回报reward，每一台机器的reward服从特定的概率分布。
2）一个赌徒有N次拉杆的机会，他的目标是使得回报reward最大化，那么他要确定这N次选择机器的顺序。显然，作为一个聪明的赌徒，他会记录下每一次得到的reward，试图找出能给出最大reward的那台机器，尽量多次数的去拉这台机器 。
3) 对于每一轮选择，主要面对的问题是Exploitation-Exploration：

• Exploitation: 以最高的预期收益拉动手臂
• Exploration: 玩其他机器以获得有关它们的预期收益的更多信息

4）得到的收益称为reward，一般假设为伯努利分布，即0或1。得到的收益与真实的最大收益（最优）（上帝视角，假设一开始就知道哪个payoff最大，那我肯定拉哪个手臂）之间的差值称为regret。

2.探索-利用问题（Exploration-Exploitation dilemma）

经典的强化学习算法，多用于处理Exploitation（利用）-Exploration（探索）（EE）权衡（trade-off）问题，即一个最优选择问题。MAB也应用于随机调度（Stochastic scheduling）问题中。

探索-利用问题（Exploration-Exploitation dilemma）:

• 仅探索（exploration-only），探索各个摇臂的奖赏均值，以相同的概率选择每一个摇臂；
• 仅利用（exploitation-only），每次选择当前平均奖赏最大的摇臂。

探索和利用两者之间是相互矛盾的，由于总的尝试次数是有限的，采用“探索”则无法每次选择最优的选项，选择“利用”则无法发现可能潜在的更优的选项，这就是强化学习中的“探索-利用窘境（Exploration-Exploitation dilemma）”所以要实现累积回报最大化，需要在“探索”和“利用”之间达到一个较好的折中。

一个问题，其中必须在竞争、选择之间以最大化其预期收益的方式分配固定的有限资源集，当每个选择的属性在分配时仅部分已知时，并且随着时间的推移可以更好地理解 或者通过为选择分配资源。

3.Bandit问题

1)基本的RL setting

在t=1,2,…,T的每个阶段中，一个bandit算法应该做如下两件事：

• 算法从 A中选择一个arm：a(t)
• 算法观察到at这个arm返回的奖励（reward）r(t)

2)Bandit问题的几类算法

经典bandit算法当中，我们要做的无非就是通过一类pull arm的策略，尽快找到比较好的“arm”（reward较高的arm），然后尽可能多的去拉这些比较好的arm就是了

• 贪心算法（uniform exploration，$ϵ$-greedy算法）无非就是永远以当前对每个arm的reward的估计直接作为依据。贪心算法（greedy algorithm）的思路非常直接，就是：使用过去的数据去估计（estimate）一个模型（model）；选择能够optimize所估计模型的动作（action），主动的探索（active exploration）不足。
  epsilon贪心算法: 每次决策时，以概率e进行仅探索（以均匀的概率随机选择一个摇臂）；以概率1-e进行仅利用（选择目前为止平均奖赏最大的摇臂）。
• UCB（upper confidence bound）算法则是考虑了置信度的问题，因此考虑的是每个arm reward的置信区间的上界。
• softmax算法
  softmax算法: 每次决策时，先计算所有摇臂的平均奖赏的softmax值，然后以这个值为摇臂的概率来选择摇臂。其中有个τ值，用来控制倾向于探索或利用的程度。

4. MAB类型

1）老虎机类型的MAB

老虎机情景是在环境不变的情况下stochastic bandit（随机MAB）

2）环境改变的MAB

如果环境改变（即环境就是随着时间/玩家的行为会发生变化）

也就是所谓的adversarial bandit就是说这些pi会被一个“对手”（也可以看成上帝）设定好。如果这是事先设定好，并且在玩家开始有动作之后也无法更改，我们叫做oblivious adversary setting; 如果这个对手在玩家有动作之后还能随时更改自己的设定，那就叫做adaptive adversary setting, 一般要做成zero-sum game了。

3）contextual MAB(cMAB)(MAB的变种)

几乎所有在线广告推送（dynamic ad display）都可以看成是cMAB问题。在这类问题中，每个arm的回报会和当前时段出现的顾客的特征（也就是这里说的context）有关。

期望的reward可以取决于外部变量。

a)线性回归模型来预测reward

假设reward和特征向量存在一个线性关系$reward=x^T\theta$
在Contextual Bandits当中，$\tilde{p}=x^T\theta$，其中$\theta$是需要学习的参数。
使用的线性回归－Ridge Regression来求解 $\theta$：

• x是观测到特征向量，如x= (荤菜，素菜，男，女，早饭，午饭，晚饭)

• 也就是reward（每道菜好吃的概率——就是你问题中想知道的结果）

输入：多次实验结果{（x1,reward1）,…, （xN,rewardN）}
优化目标：

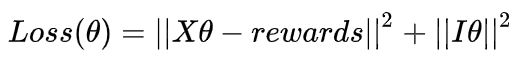
其中：

• X=[x1,…,xK]是K次实验观测的特征向量组成的矩阵，每一行代表一个特征向量
• Rewards = [reward1,…,rewardk]是K次实验的结果，reward=1/0
• ||IX||2为L2 normalization，防止过拟合，其中I为对角线矩阵

为求解$\theta$ ，对目标函数求导：

得到：

b)Bernoulli Bandit和Contextual Bandit的对比

• Bernoulli Bandit

在Bernoulli Bandit中，我们假设reward是服从伯努利分布的：

对于mean reward$\theta$：先验分布（prior distribution）是Beta分布，而每个arm reward的分布是以 $\theta$为参数Bernoulli（伯努利）分布。容易知道，在这种情况下，$\theta$ 的后验分布仍然是Beta分布

• Contextual Bandit

在Contextual Bandit中，我们假设reward和特征向量存在一个线性关系 ：

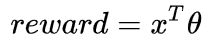
是确定性的，无法直接定义出一个概率分布来描述 的不确定性。

c）不同赌博机对回报定义的对比

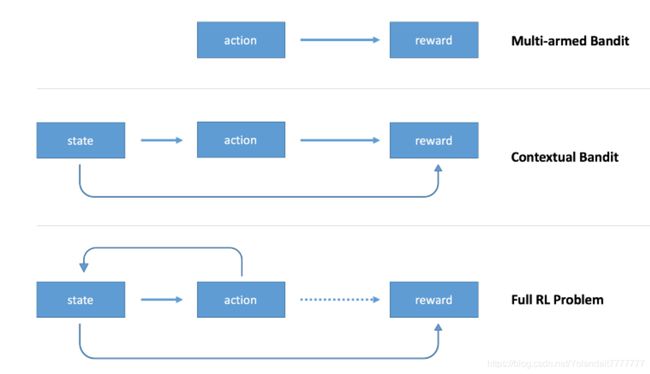
• 多臂赌博机问题中，只有行动影响回报。
  一般多臂赌博机问题里，只有一个赌博机，它可以被当做一个槽机器。我们的agent可选行动的范围就是从赌博机的多个臂中选一个拉动。通过这样做，获得一个+1或者-1的回报。当agent学会了总是选择可以返回正回报的臂去拉动时，这个问题就被认为是解决了。在这种情况下，我们可以设计一个完全忽略掉环境状态的agent，因为从各方面来看，都只有一个单一不变的状态
• 上下文赌博机问题中，状态和行动都影响回报
  上下文赌博机引入了状态的概念。状态就是对环境的一种描述；有多个赌博机；agent将需要学习如何基于环境状态来选择行动。
• 完备强化学习问题中，行动影响状态，回报可能在时间上延迟

4）Bandit with Knapsack问题

每台老虎机每天摇的次数有上限
这类问题以传统组合优化里的背包问题命名

5)Lipshitz bandit

不再有有限台机器，而有无限台（它们的reward function满足利普西茨连续性）。

5.Thompson sampling

是贝叶斯框架下在线学习的适用性算法

UCB算法和Thompson Sampling的区别:

• UCB算法——Frequentist学派
  
• Thompson Sampling——Bayesian (贝叶斯) 学派
  
  Bernoulli (伯努利)分布（以概率p的到0/1）