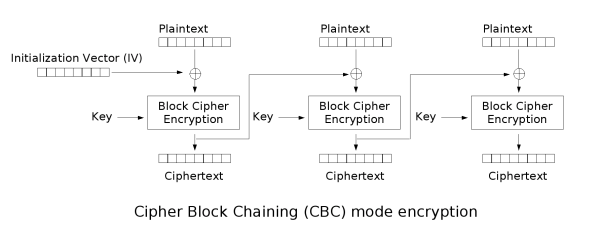公钥密码学公钥基础设施_密码学和公钥基础结构简介

公钥密码学公钥基础设施

安全通信正在Swift成为当今网络的规范。 Google Chrome计划在2018年7月开始为通过HTTP（而不是HTTPS）传输的所有网站显示“不安全”通知。 Mozilla也有类似的计划。尽管密码学变得越来越普遍，但它却变得不容易理解。让我们来加密设计并构建一个出色的解决方案，以提供并定期更新免费的安全证书，但是，如果您不了解基本概念和陷阱，那么您只是一大批热衷于货物的程序员中的另一个成员。

安全通信的属性

加密在直观上显而易见的目的是机密性 ：可以传输消息而无需费力地了解其内容。为了保密起见，我们对消息进行加密 ：给消息，我们将其与密钥配对，并产生无意义的混乱，只有通过使用相同的密钥来逆转该过程（从而对其进行解密），该混乱才能再次变得有用。假设我们有两个朋友，爱丽丝和鲍勃，以及他们爱管闲事的邻居夏娃。爱丽丝可以加密“夏娃很烦人”之类的消息，然后将其发送给鲍勃，而不必担心夏娃偷窥她。

完整性 ：信息应不受篡改。

但是，我们还有另一个问题。假设夏娃看着鲍勃打开一个标有“来自爱丽丝”的信封，里面有一封爱丽丝的消息，上面写着“再买一加仑冰淇淋”。夏娃（Eve）看到鲍勃（Bob）出去吃冰淇淋，然后回来，所以即使她不知道确切的措词，她也对消息的内容有一个大致的了解。 Bob丢弃了该消息，Eve对其进行了恢复，然后在下周的每一天每天都将一个标有“ From Alice”的信封和该消息的副本放入Bob的邮箱中。现在，聚会上的冰淇淋太多了，当鲍勃在深夜结束时将冰淇淋赠送给夏娃时，夏娃会免费带回家。额外的消息是机密的，它们的完整性是完整的，但是Bob误导了发件人的真实身份。 身份验证是知道与您通信的人实际上是他们声称的身份的属性。

信息安全还具有其他属性，但是机密性 ， 完整性和身份验证是您必须了解的三个特征。

加密和密码

加密的组成部分是什么？我们需要一个称为纯文本的消息。我们可能需要对消息进行一些初始格式化，以使其适合于加密过程（例如，如果我们使用分组密码，则将其填充到特定长度）。然后，我们采用称为密钥的秘密位序列。然后加密需要密钥和转换明文为密文。密文应该看起来像是随机噪声，并且只有使用相同的密文和相同的密钥（或者稍后我们将在非对称密码的情况下看到，在数学上相关的密钥），才能恢复明文。

密码使用密钥的位转换明文的位。由于我们希望能够解密密文，因此我们的密文也必须是可逆的。我们可以使用XOR作为简单示例。它是可逆的并且是它自己的逆（P ^ K = C; C ^ K = P），因此它既可以加密明文，也可以解密密文。一次使用XOR的微不足道的操作可用于一次性加密，但通常不切实际。但是，可以将XOR与从单个键生成随机数据的任意流的函数结合使用。像AES和Chacha20这样的现代密码就可以做到这一点。

我们称呼使用相同密钥的任何密码来加密和解密对称密码 。对称密码分为流密码和分组密码 。流密码一次通过消息运行一个位或一个字节。例如，我们的XOR密码是流密码。如果明文的长度未知（例如，来自管道或套接字的数据），则流密码很有用。 RC4是最著名的流密码，但容易受到多种攻击的攻击，并且TLS协议的最新版本（1.3）（“ HTTPS”中的“ S”）甚至不支持它。正在努力创建新的流密码，其中TLS已支持一些候选者，例如ChaCha20 。

分组密码采用固定大小的块，并使用固定大小的密钥对其进行加密。分组密码世界中当前的“山王”是高级加密标准（AES），其块大小为128位。数据不是很多，所以分组密码的模式描述了如何对任意大小的消息应用密码的分组操作。最简单的模式是电子密码簿（ECB），它接收消息，将其拆分为块（如有必要，填充消息的最后一块），然后用密钥分别加密每个块。

您可能在这里发现一个问题：如果同一块在消息中多次出现（例如，在网络流量中出现类似“ GET / HTTP / 1.1”之类的短语），并且我们使用相同的密钥对其进行加密，则会得到相同的结果结果。模式在我们的加密通信中的出现使其很容易受到攻击。

因此，存在更高级的模式，例如密码块链接（CBC），其中每个块的加密结果与下一个块的明文进行异或。第一个块的明文与随机数的初始化向量进行异或。还有许多其他模式，每种模式在安全性和速度上各有优缺点。甚至还有一些模式（例如计数器（CTR））都可以将分组密码转换为流密码。

与对称密码相反，存在非对称密码（也称为公钥密码术）。这些密码使用两个密钥：公共密钥和私有密钥。密钥在数学上相关，但仍然不同。用公钥加密的任何内容都只能用私钥解密，用私钥加密的数据可以用公钥解密。公钥被广泛分发，而私钥则被保密。如果要与给定的人进行通信，则可以使用他们的公钥来加密您的消息，只有他们的私钥才能对其进行解密。 RSA是当前不对称密码的重量级拥护者。

非对称密码的主要缺点是它们在计算上很昂贵。我们可以使用对称密码进行身份验证以加快处理速度吗？如果您仅与他人共享密钥，则可以。但这很快就分解了。假设一群人希望使用对称密码相互通信。小组成员可以为成员的每个唯一配对建立密钥，并根据接收者对消息进行加密，但是由20个人组成的小组计算出总共190对成员，每个人可以管理和保护19个密钥。通过使用非对称密码，每个人只需要保护自己的私钥，就可以访问公钥列表。

非对称密码在可以加密的数据量方面也受到限制。像分组密码一样，您必须将较长的消息分成多个部分。然后在实践中，通常使用非对称密码来建立机密的，经过身份验证的通道，然后将其用于交换对称密码的共享密钥。对称密码用于后续通信，因为它速度更快。 TLS可以完全以此方式运行。

在基础上

安全通信的核心是随机数。随机数用于生成密钥并为其他确定性过程提供不可预测性。如果我们使用的密钥是可预测的，那么我们从一开始就很容易受到攻击。随机数很难在计算机上生成，这意味着计算机将以一致的方式运行。计算机可以从诸如鼠标移动或键盘计时之类的信息中收集随机数据。但是收集随机性（称为熵）需要花费大量时间，并且需要进行额外的处理以确保均匀分布。它甚至可能涉及使用专用硬件（例如熔岩灯墙）。通常，一旦我们有了一个真正的随机值，就将其用作种子，放入加密安全的伪随机数生成器中，从相同的种子开始总是会导致相同的数字流，但重要的是数字流降了从种子不显示任何模式。在Linux内核/ dev / random和/ dev / urandom中，以这种方式运行：它们从多个来源收集熵，对其进行处理以消除偏差，创建种子，然后可以提供用于生成RSA密钥的随机数例如。

其他加密构造块

我们已经介绍了机密性，但是我还没有提到完整性或身份验证。为此，我们需要在工具箱中添加一些新工具。

第一个是密码哈希函数 。加密散列函数旨在获取任意大小的输入并产生固定大小的输出（通常称为摘要）。如果我们能找到创建相同摘要的任何两条消息，那就是冲突，使哈希函数不适合密码学。注意强调“查找”；如果我们有无限的消息世界和固定大小的输出，那么肯定会发生冲突，但是如果我们能够找到两条碰撞而没有大量计算资源投入的消息，那就太麻烦了。更糟糕的是，如果我们可以接收一条特定的消息，然后找到另一条导致冲突的消息。

同样，哈希函数应该是单向的：给定摘要，确定消息是什么在计算上不可行。这些要求分别称为耐碰撞性，第二原像电阻和原像电阻。如果满足这些要求，则摘要将充当消息的指纹。从理论上讲，没有两个人具有相同的指纹，并且您不能拿指纹并将其变回一个人。

如果我们发送消息和摘要，则收件人可以使用相同的哈希函数来生成独立的摘要。如果两个摘要匹配，则说明消息未更改。自SHA-1开始显示其年龄以来， SHA-256是当前最流行的加密哈希函数。

哈希听起来不错，但是如果有人可以篡改您的消息然后又篡改该摘要，则发送带有消息的摘要有什么好处？我们需要将哈希与我们拥有的密码混合在一起。对于对称密码，我们有消息验证码 （MAC）。 MAC以不同的形式出现，但是HMAC基于哈希。 HMAC使用密钥K和消息M，并使用具有公式H（K + H（K + M））的哈希函数H将它们混合在一起，其中“ +”是串联的。为什么要特别指定此公式？这超出了本文的范围，但是与保护HMAC本身的完整性有关。 MAC与加密消息一起发送。夏娃可以盲目地操纵消息，但是鲍勃一独立地计算出MAC并将其与他接收到的MAC进行比较，他就会意识到消息已被篡改。

对于非对称密码，我们有数字签名 。在RSA中，使用公钥加密只能使私钥解密，但反之亦然，并且可以创建一种签名。如果只有我拥有私钥并加密文档，那么只有我的公钥才能解密文档，其他人可以隐式相信我编写的文档：身份验证。实际上，我们甚至不需要加密整个文档。如果我们创建文档的摘要，则可以仅加密指纹。签名摘要而不是整个文档更快，并且可以解决可以使用非对称加密进行加密的邮件大小周围的一些问题。收件人解密摘要，独立计算消息的摘要，然后比较两者以确保完整性。对于其他非对称密码，用于数字签名的方法也有所不同，但是使用公钥来验证签名的概念仍然存在。

放在一起

既然我们拥有了所有主要部分，我们就可以实现一个具有我们所要寻找的所有三个属性的系统。爱丽丝选择了一个对称的秘密密钥，并用鲍勃的公钥对其进行加密。然后，她对所得密文进行哈希处理，并使用她的私钥对摘要进行签名。鲍勃接收密文和签名，计算密文的摘要，并将其与他使用爱丽丝的公钥验证的签名中的摘要进行比较。如果两个摘要相同，则他知道对称密钥具有完整性并已通过身份验证。他使用自己的私钥解密密文，并使用Alice发送给他的对称密钥使用HMAC与每个消息进行机密通信，以确保完整性。这里没有防止消息重放的保护措施（如夏娃在冰淇淋灾难中所看到的）。要解决该问题，我们需要某种“握手”，可用于建立随机的，短暂的会话标识符。

密码世界是广阔而复杂的，但是我希望本文能够为您提供有关其使用的核心目标和组件的基本思维模型。有了扎实的概念基础，您就可以继续学习更多。

感谢Hubert Kario，Florian Weimer和Mike Bursell对本文的帮助。

翻译自: https://opensource.com/article/18/5/cryptography-pki