智能计算系统课程笔记05:编程框架机理

TensorFlow设计原则

TensorFlow的设计原则为:高性能,易开发,可移植

1. 高性能

   • TensorFlow中的算子,设计过程中已经针对底层硬件架构进行了充分的优化.

   • 针对生成的计算图,TensorFlow又提供了一系列的优化操作,以提升计算图的运行效率.

   • TensorFlow调度器可以根据网络结构特点,并发运行没有数据依赖的节点.

   例如对于下面的例子:

   import tensorflow as tf
   
   a = tf.constant(1.0)
   b = tf.constant(2.0)
   c = tf.sin(a)
   d = tf.cos(b)
   e = tf.add(c, d)
   
   with tf.Session() as sess:
       sess.run(e)
   

   上面例子中c和d没有依赖关系,可以并发执行.

2. 易开发

   • TensorFlow针对现有的多种深度学习算法,提取了大的共性运算,并封装成算子.

   • 用户使用TensorFlow进行算法开发时,能够直接调用这些算子,很方便的实现算法.

3. 可移植

   • TensorFlow可工作于各种类型的异构系统.
   • 对每个算子（例如矩阵乘法）需提供在不同设备上的不同底层实现.
   • 通过上述机制,使得统一的用户程序可以在不同硬件平台上执行.

TensorFlow计算图机制

计算图的自动求导

• 深度学习中通常采用梯度下降法来更新模型参数.

• 梯度计算比较直观,但对于复杂模型,手动计算梯度非常困难

• 目前大部分深度学习框架均提供自动梯度计算功能

• 用户只需描述前向计算的过程,由编程框架自动推导反向计算图,完成导数计算

常用的求导方法

常用的求导方法包括: 手动求解法,数值求导法,符号求导法,自动求导法.

手动求解法

即传统的反向传播算法: 手动用链式法则求解出梯度公式,代入数值,得到最终梯度值.

缺点:

• 对于大规模的深度学习算法,手动用链式法则进行梯度计算并转换成计算机程序非常困难.
• 需要手动编写梯度求解代码.
• 每次修改算法模型,都要修改对应的梯度求解算法.

数值求导法

利用导数的原始定义求解
$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
优点:

• 易操作
• 可对用户隐藏求解过程

缺点:

• 计算量大,求解速度慢
• 可能引起舍入误差和截断误差

符号求导法

利用求导规则来对表达式进行自动操作,从而获得导数.

常见求导规则:
$$\begin{gathered} \frac{d}{dx}(f(x)+g(x))=\frac{d}{dx}f(x)+\frac{d}{dx}g(x) \\ \frac{d}{dx}(f(x)g(x))=(\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x)) \\ \frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f^{\prime }(x)g(x)-f(x)g^{\prime }(x)}{g(x{)}^2} \end{gathered}$$

缺点: 表达式膨胀问题

自动求导法

• 上述求导方法的对比:

  • 数值求导法: 一开始直接代入数值近似求解
  • 符号求导法: 直接对代数表达式求解,最后才代入问题数字
  • 自动求导法: 介于数值求导和符号求导的方法
  对基本算子应用符号求导法

  代入数值,保留中间结果

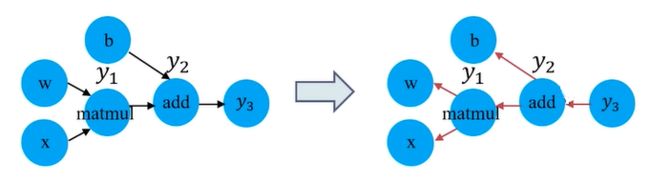
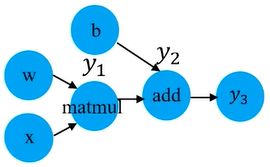
• 计算图结构天然适用于自动求导:

  计算图将多输入的复杂计算表达成了由多个基本二元计算组成的有向图,并保留了所有中间变量,有助于程序自动利用链式法则进行求导.

  y1

  y2

  w

  x

  b

  matmul

  add

  y3

• 优点:

  • 灵活,可以完全向用户隐藏求导过程.
  • 只对基本函数运用符号求导法,因此可以灵活结合编程语言的循环结构、条件结构等.

• 下面例子展示TensorFlow中注册Sin(x)函数反向求导方法:

  @ops.RegisterGradient("Sin")
  def _SinGrad(op, grad):
      """Returns grad * cos(x) """
      x = op.inputs[0]
      with ops.control_dependencies([grad]):
          x = math_ops.conj(x)
          return grad * math_ops.cos(x)
  

• TensorFlow会自动生成对应的反向计算节点,并将其加入到计算图中.

  v1 = tf.Variable(0.0, name="v1")
  v2 = tf.Variable(0.0, name="v2")
  loss = tf.add(tf.sin(v1), v2)
  sgd = tf.train.GradientDescentOptimizer(0.01)
  grads_and_vars = sgd.compute_gradient(loss)
  

  

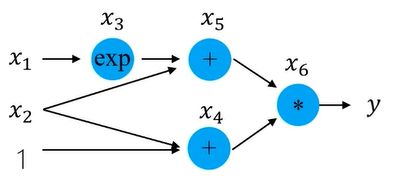
• 计算过程: 分两步执行

  1. 原始函数建立计算图,数据正向传播,计算出中间节点$x_i$,并记录计算图中的节点依赖关系.

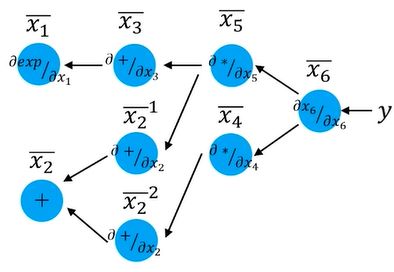
  2. 反向遍历计算图,计算输出对于每个节点的导数

     $$\overline{x_i}=\frac{\partial y_j}{\partial x_i}$$

  对于前向计算中一个数据($x_i$)连接多个输出数据($y_j$,$y_k$)的情况,自动求导中,将这些输出数据相对于该数据的导数累加.
  $$\overline{x_i}=\overline{y_j}\frac{\partial y_j}{\partial x_i}+\overline{y_k}\frac{\partial y_k}{\partial x_i}$$

  • 示例: 对于函数$f(x_1,x_2)=(e^{x_1}+x_2)(x_2+1)$

    	前向计算	反向计算
    计算过程
    示意图

四种求导方法的对比

方法	对图的遍历次数	精度	备注
手动求解法	$N_A$	高	实现复杂
数值求导法	$n_i+1$	低	计算量大,速度慢
符号求导法	$N_A$	高	表达式膨胀
自动求导法	$n_o+1$	高	对输入维度较大的情况优势明显

其中:

• $n_i$表示要求导的神经网络层的输入变量数,包括$w$、$x$、$b$.
• $n_o$表示神经网络层的输出个数.

检查点机制

• 在模型训练过程中,使用tf.train.Saver()来保存模型中的所有变量.

  # 实例化Saver对象
  saver = tf.train.Saver()
  
  with tf.Session() as sess:
      sess.run(tf.global_variables_initializer())
      for step in range(1000000):
          # 执行模型训练
          sess.run(training_op)
          if step % 1000 == 0:
              # 将训练得到的变量值保存到检查点文件中
              saver.save(sess, './ckpt/nfiy-model')
  

• 当需要基于某个checkpoint继续训练模型参数时,需要从.ckpt文件中恢复出已保存的变量.

  同样使用tf.train.Saver()来恢复变量,恢复变量时不需要先初始化变量.

  # 实例化Saver对象
  saver = tf.train.Saver()
  
  with tf.Session() as sess:
      # 找到存储变最值的位置
      ckpt = tf.train.latest_checkpoint(model_path)
      # 恢复变量
      saver.restore(sess, ckpt)
      print(sess.run(weights))
  

• TensorFlow通过向计算图中插入Save节点及其关联节点来完成保存模型的功能;在恢复模型时,也是通过在计算图中插入Restore节点及其关联节点来完成.

  

TensorFlow 中的控制流

• TensorFlow中使用控制流算子来实现不同复杂控制流场景.

• 通过引入少量简单基础操作,为多样的TensorFlow应用提供丰富的控制流表达.

• 在TensorFlow中,每一个操作都会在一个执行帧中北执行,控制流操作负责创建和管理这些执行帧.

5个基本的控制流算子

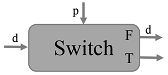
1. Switch: 一个Switch操作根据控制输入p的布尔值,将一个输入张量d推进到某一个输出(二选一).

   

2. Merge: Merge操作将它的其中一个输入推向输出.当一个Merge操作的任意一个输入准备好之后,Merge操作就会执行.

   

3. Enter(name): Enter操作将它的输入推向名为name的执行帧.

   

4. Exit: Exit操作,将一个张量从一个子执行帧推向它的辅执行帧.它的作用时将张量从子执行帧返回给父执行帧.

   

5. NextIteration: NextIteration操作将一个张量从当前执行帧的一轮迭代传递到下一轮迭代.

   在一个执行帧内部可能有多个NextIteration操作.当执行帧的第N轮执行的第一个NextIteration操作开始执行时,TensorFlow的运行时开始执行第N+1轮的迭代.

   当更多的张量通过了NextIteration操作进入新的执行轮次时,新执行伦茨中更多的操作就会开始运行.当输入准备完成之后,NextIteration操作开始执行.

   

控制流结构的编译

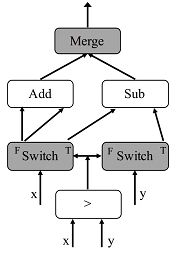
1. 条件表达式tf.cond(pred, true_fn, false_fn):

   以条件表达式tf.cond(x > y, lambda: tf.subtract(x, y), lambda: tf.add((x, y)))为例:

   

   # 添加Switch节点
   switch_f, switch_t = Switch(pred, pred)
   # 创建Switch为真时的环境
   ctx_t = MakeCondCtx(pred, switch_t, branch=1)
   # 创建Switch为真时的计算图
   res_t = ctx_t.Parse(true_fn)
   # 创建Switch为假时的环境
   ctx_f = MakeCondCtx(pred, switch_f, branch=0)
   # 创建Switch为假时的计算图
   res_f = ctx_tf.Parse(false_fn)
   # 将两个分支结果合并到一起
   rets = [Merge([f, t]) for(f, t) in zip(res_f, res_t)]
   

2. 循环操作tf.while_loop_v2(cond, body, loop_vars):

   以循环操作tf.while_loop(lambda i: i < 16, lambda i: tf.multiply(i, 2), [4])

   

   # 创建环境
   while_ctx = WhileContext()
   while_ctx.Enter()
   # 为每个循环变暈添加一个Enter节点
   enters = [Enter(x, frame_name) for x in loop_vars]
   # 添加Merge节点,Merge节点的第二个输入稍后会被更新
   merges = [Merge([x, x]) for x in enters]
   # 构建循环子图
   pred_results = pred(*merges)
   # 添加Switch节点
   switchs = [Switch(x, pred_result) for x in merges]
   # 构建循环体
   body_res = body(*[x[1] for x in switchs])
   # 添加Nextltreation节点
   nexts = [Nextlteration(x) for x in body_res]
   # 构建循环迭代 
   for m, n in zip(merge_vars, nexts):
       m.op.update(l, n)
   # 添加退出节点
   exits = [Exit(x[0]) for x in switchs]
   while_ctx.Exit()
   

计算图的执行模式

• client: 通过session接口与master和worke接口通信.

  worker可以是一个,也可以是多个.

• master: 控制所有的worker按照计算图执行.

• worker: 每一个worker负责一个或多个计算设备的仲裁访问,并根据master的指令,执行这些计算设备中 的计算图节点.

• 设备: 可以是CPU核或GPU卡.

简单示例:

import tensorflow as tf

x = tf.constant(8)
y = tf.constant(9)
z = tf.multiply(x, y)

with tf.Session() as sess:
    put_z = sess.run(z)

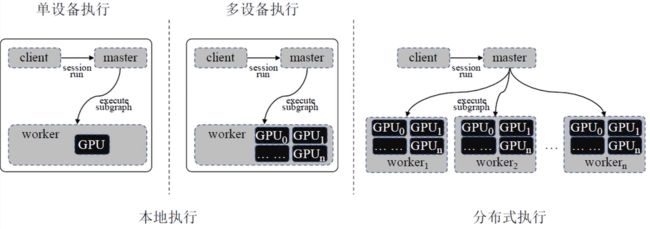
具体的执行模式有: 本地单设备执行, 本地多设备执行, 分布式执行.

1. 本地单设备执行:

   [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yiZz7Mwx-1590138801492)(image-20200522122257519 - 副本.png)]

   最简单的执行场景:适用于一个worker进程中仅包含一个设备的情况.在该情况下:

   • 计算图按照节点之间的依赖关系顺序执行.
   • 每个节点有一个计数器,记录了其依赖节点中尚未执行的节点数量,当一个节点执行完成,则其所有依赖节点的计数器计数递减.
   • 当计数器计数为0时,则该节点可以执行,并将其添加到就绪队列中.

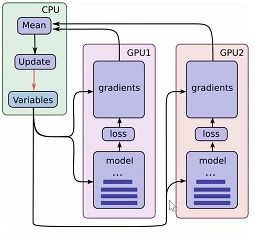
2. 本地多设备执行:

   

   • CPU作为参数服务器,用于保存参数和变量、计算梯度平均等.
   • GPU作为worker,用于模型训练.

   模型训练过程:

   1. 在本地将数据切分为一个一个batch.
   2. 把数据分别送到多个GPU进行模型训练,每个GPU分配到不同batch的数据
   3. 每个GPU分别对自己的batch训练,求loss得到梯度,把梯度送回到CPU进行模型平均
   4. CPU接收GPU传来的梯度,进行梯度平均,更新参数.
   5. GPU更新参数.
   6. 重复2-5直到模型收敛

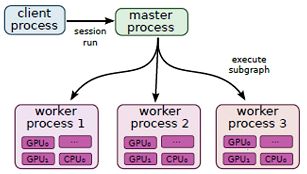
3. 分布式执行:

   

   • 该模式下,client、master和worker可以工作于不同机器上的不同进程中

   • 该模式兼容本地多设备执行模式.

计算图本地执行

计算图本地执行的过程包括: 计算图剪枝,计算图分配,计算图优化,计算图切分.

计算图剪枝

目的: 得到本地运行的最小子图.

包括:

• 为输入输出建立与外界的交互:

  • 通过FunctionCallFrame函数调用帧来解决输入输出值传递的问题.
  • 在每个输入节点前插入Arg节点,所有的输入节点连接到Source节点上,并通过控制依赖边相连.
  • 在每个输出节点后面加入RetVal节点,所有的输出节点连接到Sink节点上,也通过控制依赖边相连,最终形成完整的计算图.

  这种函数调用帧类似于函数调用时的栈帧.

  Source和Sink是两个特殊的节点,Source节点的入度为0,Sink节点的出度为0.

• 去除与最终输出节点无关的节点和边:

  • 从输出节点开始进行宽度搜索遍历,删除没有接触到的节点和边.
  • 将每个连通图中入度为0的节点通过控制依赖边与Source节点相连,出度为0的节点通过控制依赖边和Sink节点相连.

计算图分配

计算图分配解决了多设备运行环境中,对计算图中的每个节点如何分配计算设备的问题.

使用开销模型cost model算法分配计算图中的节点,该算法考虑图中每个节点的输入输出tensor的数据量、每个节点的预计计算时间.

算法执行过程:

1. 从计算图起始点开始遍历.
2. 对于遍历中的每个节点,考虑其可行的设备集合.
3. 如果设备不提供实现特定操作的内核,则设备不可行.
4. 如果某个节点具有多个可行设备,则采用贪心算法,检查该节点在所有可行设备上的完成时间,将最快完成的设备分配给该节点.
5. 重复2-4直到遍历完成整个图.

计算图优化

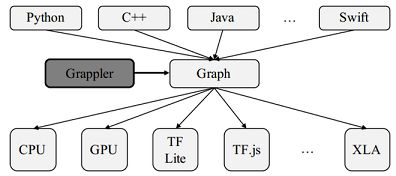
• TensorFlow中的图优化由Grappler模块来实现.
• 通过图优化,可以根据不同的硬件结构调整计算调度策略,从而获得更快的计算速度和更高的硬件利用率.
• 也能减少推断过程中所需的峰值内存,从而运行更大的模型.

计算图优化的手段包括:常量折叠ConstFold,算数优化Arithmetic,布局优化Layout,算子融合Remapper.

1. 常量折叠ConstFold: 有的常数节点可以被提前计算,用得到的结果生成新的节点 来代替原来的常数节点.主要由三个关键函数组成:

   1. MaterializeShapes: 处理与Shape相关的节点.
   2. FoldGraph: 对每个节点的输入进行检测,如果均为Const节点,则提前计算出值来完整替换当前节点
   3. SimplifyGraph: 简化节点中的常量运算.

2. 算数优化Arithmetic: 包括公共子表达式消除,算术简化.

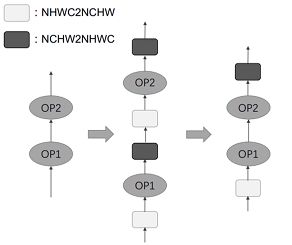
3. 布局优化Layout:

   TensorFlow中默认采用NHWC格式,而GPU中使用NCHW格式.

   两个连续的GPU计算节点之间的连续NCHW2NHWC和NHWC2NCHW转换应互相抵消去除.

   

计算图切分和设备通信

• 完成每个节点的设备分配后,将整个计算图按照所分配设备分成若干子图,每个设备一张子图.

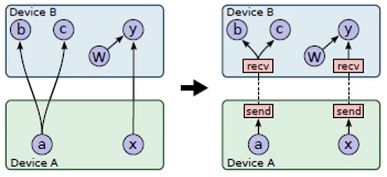
• 对于跨设备通信的边,执行如下操作:
  1. 将跨设备的边删掉.
  2. 在设备边界插入send和recv节点.
  3. 在设备A对应的子图中,增加x节点到send节点的边.
  4. 在设备B对应的子图中,增加recv节点到y节点的边.
  5. 插入send和recv节点时,规定单个设备上特定张量的多个用户使用单个recv节点,如节点b、c,从而确保所需的张量在设备之间只传输一次.
  6. 执行计算图时,通过send和recv节点来实现跨设备的数据传输

计算图的分布式执行

• 神经网络规模及数据规模指数型增加

• 为了有效提高神经网络训练效率,降低训练时间,在模型训练中普遍采用分布式技术.
• 分布式技术:将一个大的神经网络模型,拆分成许多小的部分,同时分配在多个节点上进行计算.
• 目前主流的深度学习框架均支持分布式技术

分布式通信

分为两类: 点到点通信（Point-to-Point Communication)和集合通信(Collective Communication).

TensorFlow中实现了集合通信的基本算子:

• all_sum: 将所有的输入张量进行累加操作,并将累加结果广插给所有的出张量.
• all_prod: 将所有的输入张量进行乘法操作,并将乘法结果广播给所有的输出张量.
• all_min: 将所有的输入张量进行取最小值操作,并将该结果广播给所有的输出张量.
• all_max: 将所有的输入张量进行取最大值操作,并将该结果广播给所有的输出张量.
• reduce_sum: 将所有的输入张量进行累加操作f并返回这个结果.
• broadcast: 将输入张量广播给所有的设备.

容错机制

• 为了确保分布式系统的稳定性,TensorFlow中增加了错误检查和容错机制.
• 一方面检查Send和Recv节点传输的正确性,一方面定期检查每个工作机的状态.
• 检查到错误时,计算图执行过程会停止并重启.
• TensorFlow在训练过程中会保存中间状态,用于立即恢复到出错前的状态.