玩转数据结构——第八章：线段树(区间树)
线段树(Segment Tree)
内容概览：
一、什么是线段树？
二、线段树的基础表示
三、创建线段树
四、线段树中的区间查询
五、LeetCode上线段树相关的问题
六、线段树的更新操作
七、线段树更多相关的问题
为什么要使用区间树？
- 对于给定区间
- 更新：更新区间中一个元素或者一个区间的值
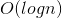，数组的实现是
级别 - 查询：查询一个区间[i,j]的最大值，最小值，或者区间数字和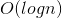，数组的实现是级别
一、什么是线段树？
每一个节点存储一个线段或一个区间响应的信息
二、线段树基础表示
- 线段树不是一定完全二叉树或满二叉树
- 线段树是一个平衡二叉树(对于整颗二叉树的叶子节点的最大的深度和它最小的深度差最大不超过1 )
- 堆也是一个平衡二叉树(完全二叉树一定是平衡二叉树)
- 二分搜索树不是平衡二叉树
- 用数组实现线段树：
三、线段树的创建
代码实现：
/**
* 使用数组实现线段树
* 当要存储n个元素时，需要开辟一个4*n的空间的数组来做线段树
*
* @param
*/
public class SegmentTree {
private E[] data;
private E[] tree;//实现线段树的数组
private Merger merger;//实现区间的融合功能
//带参构造，用户传进来数组的静态长度
public SegmentTree(E[] arr, Merger merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++)
data[i] = arr[i];
//数组实现线段树要的静态长度是4倍的n元素个数
tree = (E[]) new Object[4 * arr.length];
//tree初始是从0开始，[0,n-1]的数
buildeSegmentTree(0, 0, arr.length - 1);
}
//有多少个元素
public int getSize() {
return data.length;
}
//获取这个位置的元素
public E get(int index) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("index is Illegal");
return data[index];
}
//返回完全二叉树的数组中表示中，一个索引的元素的左孩子的索引
private int leftChild(int index) {
return 2 * index + 1;
}
//返回完全二叉树的数组中表示中，一个索引的元素的右孩子的索引
private int rightChild(int index) {
return 2 * index + 2;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append('[');
for (int i = 0; i < tree.length; i++) {
if (tree[i] != null)
res.append(tree[i]);
else
res.append("null");
if (i != tree.length - 1)
res.append(",");
}
res.append(']');
return res.toString();
}
} 融合器接口：
/**
* 融合器
* @param
*/
public interface Merger {
E merge(E a,E b);
}
递归实现创建线段树：
//在treeIndex的位置创建表示区间[l..r]的线段树
private void buildeSegmentTree(int treeIndex, int l, int r) {
//递归到底的
if (l == r) {
tree[treeIndex] = data[l];
return;
}
//左右子树在数组中对应的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = l + (r - l) / 2; //找到l，f中间的位置
//[l,mid]、[mid+1,r] 一直递归
buildeSegmentTree(leftTreeIndex, l, mid);
buildeSegmentTree(rightTreeIndex, mid + 1, r);
//用户直接决定将这两个区间的数进行怎么样的融合
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
System.out.println( tree[treeIndex]);
}测试：
public static void main(String[] args) {
Integer[] nums = {-2, 0, 3, -5, 2, -1};
// SegmentTree segmentTree = new SegmentTree<>(nums, new Merger() {
// @Override
// public Integer merge(Integer a, Integer b) {
// return a>b?a:b;//定义线段树每一个区间a，b实现什么融合，这里是区间的数相加起来
// }
// });
//使用拉姆达表达式返回区间的累加和
SegmentTree segmentTree = new SegmentTree<>(nums, (a, b) -> a+b);
//使用拉姆达表达式返回区间的最大值
SegmentTree segmentTree1 = new SegmentTree<>(nums, (a, b) -> a>b?a:b);
segmentTree.get(2);
System.out.println("每个区间的累加和："+segmentTree);
System.out.println("每个区间的最大值；"+segmentTree1);
} 结果
/**
-2,0,3,-5,-2,-1 n表示null
/ \ / \
-2,0 3 -5,2 -1
/ \ /\ / \ / \
-2 0 n n -5 2 n n
/ \ / \
n n n n
merger怎么定义，就定义每一个区间实现什么功能，上面下面实现的是累加功能
**/
每个区间的累加和：[-3,1,-4,-2,3,-3,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]
每个区间的最大值；[3,3,2,0,3,2,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]四、线段树中的区间查询
//返回区间[queryL,queryR]的值
public E query(int queryL,int queryR){
//边界检查
if(queryL<0 ||queryL>=data.length||
queryR<0||queryR>=data.length||queryL>queryR)
throw new IllegalArgumentException("Index is illegl");
return query(0,0,data.length-1,queryL,queryR);
}
//在以treeId为根的线段树中[l..r]范围里，搜索区间[queryL,queryR]的值
private E query(int treeIndex,int l,int r,int queryL,int queryR){
//递归到底的情况
if(l==queryL&&r==queryR){
return tree[treeIndex];
}
int mid=l+(r-l)/2;
int leftTreeIndex=leftChild(treeIndex);
int rightTreeIndex=rightChild(treeIndex);
if(queryL>=mid+1)//[0,3]查[2,3],mid=1,mid+1>=2,即只关心右孩子节点即可
return query(rightTreeIndex,mid+1,r,queryL,queryR);
else if(queryR<=mid)//用户要查询的区间，只在左孩子这边
return query(leftTreeIndex,l,mid,queryL,queryR);
//如果用户关心的区间有一部分落在左孩子，一部分落在右孩子
//[0,4],要查询[1,3]
//左边[0,1] 右边[3,4]
E leftResult=query(leftTreeIndex,l,mid,queryL,mid);//query(0,0,2,1,2)在[0,2]中查找[1,2]
E rightResult=query(rightTreeIndex,mid+1,r,mid+1,queryR);//query(2,3,4,3,3)在[3,4]中查找[3]
//融合这个区间
return merger.merge(leftResult,rightResult);
}
测试：
public static void main(String[] args) {
Integer[] nums = {-2, 0, 3, -5, 2, -1};
// SegmentTree segmentTree = new SegmentTree<>(nums, new Merger() {
// @Override
// public Integer merge(Integer a, Integer b) {
// return a>b?a:b;//定义线段树每一个区间a，b实现什么融合，这里是区间的数相加起来
// }
// });
//使用拉姆达表达式返回区间的累加和
SegmentTree segmentTree = new SegmentTree<>(nums, (a, b) -> a+b);
//使用拉姆达表达式返回区间的最大值
SegmentTree segmentTree1 = new SegmentTree<>(nums, (a, b) -> a>b?a:b);
System.out.println("每个区间的累加和："+segmentTree);
System.out.println("每个区间的最大值；"+segmentTree1);
//查询操作,查询[0,2]区间的和
int sum=segmentTree.query(0,2);
//查询操作，查询[1,3]区间的最大值
int maxNum=segmentTree1.query(1,3);
System.out.println("这个区间的和是:"+sum);
System.out.println("[1,3]这个区间的最大值是:"+maxNum);
} 结果：
/**
-2,0,3,-5,-2,-1 n:null
/ \ / \
-2,0 3 -5,2 -1
/ \ /\ / \ / \
-2 0 n n -5 2 n n
/ \ / \
n n n n
merger怎么定义，就定义每一个区间实现什么功能，上面下面实现的是累加功能
**/
每个区间的累加和：[-3,1,-4,-2,3,-3,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]
每个区间的最大值；[3,3,2,0,3,2,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]
这个区间的和是:1
这个区间的最大值是:3五、LeetCode上线段树相关的问题
https://mp.csdn.net/postedit/82942962
六、更新操作
//将index位置的值，更新为e
public void set(int index, E e) {
//边界检查
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("index is illegal");
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
//在以treeindex为根的线段树中更新index的值e
private void set(int treeIndex, int l, int r, int index, E e) {
if (r == l) {
tree[treeIndex] = e;
return;
}
int mid = l + (r + l) / 2;
int lefTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if (index >= mid + 1) {//只有在右子树去寻找
set(rightTreeIndex, mid + 1, r, index, e);
} else
set(lefTreeIndex, l, mid, index, e);
//最后面还有更新它的父辈
tree[treeIndex] = merger.merge(tree[lefTreeIndex], tree[rightTreeIndex]);
}